WikiDer > Берманский поток - Википедия

В динамика жидкостей, Берманский поток представляет собой устойчивый поток, создаваемый внутри прямоугольного канала с двумя равными пористый стены. Концепция названа в честь ученого Абрахама С. Бермана, сформулировавшего проблему в 1953 году.^[1]

Описание потока

Рассмотрим прямоугольный канал, ширина которого намного больше высоты. Пусть расстояние между верхней и нижней стенкой будет ${ displaystyle 2h}$ и выберем координаты так, чтобы ${ Displaystyle х = 0, y = 0}$ лежит посередине между двумя стенами, с ${ displaystyle y}$ точки, перпендикулярные плоскостям. Пусть обе стенки будут пористыми с одинаковой скоростью ${ displaystyle V}$. Тогда уравнение неразрывности и Уравнения Навье – Стокса для несжимаемой жидкости стать^[2]

${ displaystyle { begin {align} { frac { partial u} { partial x}} + { frac { partial v} { partial y}} & = 0 u { frac { partial u} { partial x}} + v { frac { partial u} { partial y}} & = - { frac {1} { rho}} { frac { partial p} { partial x }} + nu left ({ frac { partial ^ {2} u} { partial x ^ {2}}} + { frac { partial ^ {2} u} { partial y ^ {2 }}} right), u { frac { partial v} { partial x}} + v { frac { partial v} { partial y}} & = - { frac {1} { rho}} { frac { partial p} { partial y}} + nu left ({ frac { partial ^ {2} v} { partial x ^ {2}}} + { frac { partial ^ {2} v} { partial y ^ {2}}} right) end {align}}}$

с граничными условиями

${ displaystyle u (x, pm h) = 0, quad left ({ frac { partial u} { partial y}} right) _ {y = 0} = 0, quad v (x , 0) = 0, quad v (x, pm h) = V}$

Граничные условия в центре обусловлены симметрией. Поскольку решение симметрично над плоскостью ${ displaystyle y = 0}$, достаточно описать только половину потока, скажем, для ${ displaystyle y> 0}$. Если мы ищем ${ displaystyle v}$ решение, которое не зависит от ${ displaystyle x}$, уравнение неразрывности диктует, что горизонтальная скорость ${ displaystyle u}$ может быть не более чем линейной функцией ${ displaystyle x}$.^[3] Поэтому Берман ввел следующую форму:

${ displaystyle eta = { frac {y} {h}}, quad psi (x, eta) = [h { bar {u}} _ {o} -xV] f ( eta), quad u = left (u_ {o} - { frac {Vx} {h}} right) f '( eta), quad v = Vf ( eta)}$

куда ${ Displaystyle и_ {о} ( eta)}$ - произвольная функция, и со временем она будет исключена из проблемы. Подстановка этого в уравнение импульса приводит к

${ displaystyle { begin {align} - { frac {1} { rho}} { frac { partial p} { partial x}} & = left ({ bar {u}} _ {о } - { frac {Vx} {h}} right) left (- { frac {V} {h}} [f '^ {2} -ff' '] - { frac { nu} { h ^ {2}}} f '' ' right), - { frac {1} { rho}} { frac { partial p} { partial eta}} & = nu { frac {dv} {d eta}} - { frac { nu} {h}} { frac {d ^ {2} v} {d eta ^ {2}}} end {align}}}$

Берманский поток

Дифференцируя второе уравнение по ${ displaystyle x}$ дает ${ Displaystyle partial ^ {2} p / partial x partial eta = 0}$ это можно подставить в первое уравнение после взятия производной по ${ displaystyle eta}$ что приводит к

${ displaystyle f ^ {iv} + operatorname {Re} (f '^ {2} -ff' ')' = 0}$

куда ${ displaystyle operatorname {Re} = Vh / nu}$ это Число Рейнольдса. Интегрируя один раз, получаем

${ displaystyle f '' '+ operatorname {Re} (f' ^ {2} -ff '') = C}$

с граничными условиями

${ Displaystyle f (0) = f '' (0) = f (1) -1 = f '(1) = 0}$

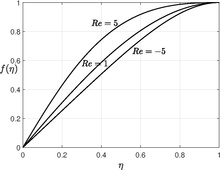
Это нелинейное обыкновенное дифференциальное уравнение третьего порядка требует трех граничных условий, а четвертое граничное условие заключается в определении постоянной ${ displaystyle C}$. и это уравнение имеет несколько решений.^[4][5] На рисунке показано численное решение для низкого числа Рейнольдса, решение уравнения для большого числа Рейнольдса не является тривиальным вычислением.

Смотрите также

• Поток Тейлора – Кулика

Рекомендации