WikiDer > Трансляция (параллельная схема)
Транслировать примитив коллективного общения в параллельное программирование Распространение программных инструкций или данных по узлам кластера является обратной операцией сокращения.[1] Операция широковещания широко используется в параллельных алгоритмах, таких как умножение матрицы на вектор,[1] Гауссово исключение и кратчайшие пути.[2]
В Интерфейс передачи сообщений осуществляет трансляцию в MPI_Bcast.[3]
Определение
Сообщение длины n должны быть распределены от одного узла ко всем другим узлы.
время, необходимое для отправки одного байта.
это время, которое требуется сообщению, чтобы добраться до другого узла, независимо от его длины.
Следовательно, время отправки пакета от одного узла к другому равно .[1]
- количество узлов и количество процессоров.
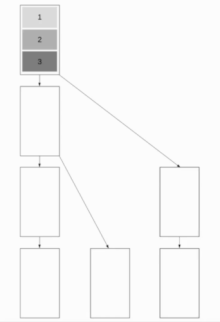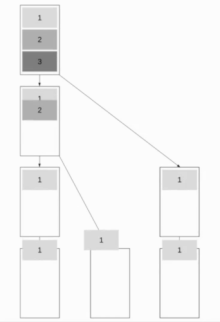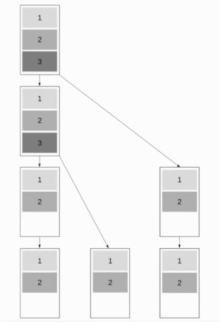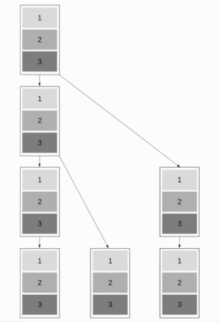
Трансляция биномиального дерева [4]
С Binomial Tree Broadcast все сообщение отправляется сразу. Каждый узел, который уже получил сообщение, отправляет его дальше. Это число растет экспоненциально, поскольку на каждом временном шаге количество отправляющих узлов удваивается. Алгоритм идеален для коротких сообщений, но не подходит для более длинных, как в то время, когда происходит первая передача и только один узел занят.
Отправка сообщения всем узлам занимает время, которое приводит к выполнению
Сообщение Mя бы := узел номерп := номер из узлыесли я бы > 0 blocking_receive Mза (я := потолок(log_2(п)) - 1; я >= 0; я--) если (я бы % 2^(я+1) == 0 && я бы + 2^я <= п) Отправить M к узел я бы + 2^яЛинейное конвейерное вещание[4]
Сообщение разбито на пакеты и отправлять по частям с узла узел . Время, необходимое для распространения первой части сообщения, составляет Посредством чего время, необходимое для отправки пакета от одного процессора к другому.
Отправка всего сообщения занимает .
Оптимально выбрать в результате время выполнения примерно
Время выполнения зависит не только от длины сообщения, но и от количества процессоров, играющих роли. Этот подход эффективен, когда длина сообщения намного превышает количество процессоров.
Сообщение M := [m_1, m_2, ..., m_n]я бы = узел номерза (я := 1; я <= п; я++) в параллельно если (я бы != 0) blocking_receive m_i если (я бы != п) Отправить m_i к узел я бы + 1Конвейерная рассылка двоичного дерева[2][4]
Этот алгоритм сочетает в себе широковещательную рассылку биномиального дерева и линейную конвейерную рассылку, благодаря чему алгоритм хорошо работает как для коротких, так и для длинных сообщений. Цель состоит в том, чтобы как можно больше узлов работало, сохраняя при этом возможность быстрой отправки коротких сообщений. Хороший подход - использовать Деревья Фибоначчи для разделения дерева, что является хорошим выбором, поскольку сообщение не может быть отправлено обоим дочерним элементам одновременно. Это приводит к двоичное дерево структура.
В дальнейшем мы будем предполагать, что общение полнодуплексный. В Дерево Фибоначчи структура имеет глубину около Посредством чего то Золотое сечение.
В результате время выполнения . Оптимально .
Это приводит к времени выполнения .
Сообщение M := [m_1, m_2, ..., m_k]за я = 1 к k если (hasParent()) blocking_receive m_i если (hasChild(left_child)) Отправить m_i к left_child если (hasChild(right_child)) Отправить m_i к right_childТрансляция двух деревьев (трансляция 23) [5][6][7]
Определение
Этот алгоритм направлен на устранение некоторых недостатков моделей древовидной структуры с конвейерами. Обычно в моделях древовидной структуры с конвейерами (см. Методы выше) листья получают только свои данные и не могут участвовать в отправке и распространении данных.
Алгоритм одновременно использует два бинарные деревья чтобы общаться. Эти деревья будут называться деревьями A и B. бинарные деревья выходных узлов относительно больше, чем внутренних. Основная идея этого алгоритма состоит в том, чтобы сделать листовой узел дерева A внутренним узлом дерева B. Он также выполняет ту же техническую функцию на противоположной стороне от дерева B до дерева A. Это означает, что два пакета отправляются и принимаются внутренними узлами и отправляются на разных этапах.
Строительство дерева
Количество шагов, необходимых для построения двух параллельно работающих бинарные деревья зависит от количества процессоров. Как и в случае с другими структурами, один процессор может быть корневым узлом, который отправляет сообщения двум деревьям. Нет необходимости устанавливать корневой узел, потому что нетрудно распознать, что направление отправки сообщений в двоичное дерево обычно сверху вниз. Нет ограничений на количество процессоров для сборки двух бинарные деревья. Пусть высота комбинированного дерева будет час = ⌈Log (п + 2)⌉. Дерево A и B может иметь высоту . Особенно, если количество процессоров соответствует , мы можем сделать деревья с обеих сторон и корневой узел.
Чтобы построить эту модель эффективно и легко с полностью построенным деревом, мы можем использовать два метода, называемые «Сдвиг» и «Зеркальное отображение», чтобы получить второе дерево. Предположим, что дерево A уже смоделировано, а дерево B должно быть построено на основе дерева A. Мы предполагаем, что у нас есть процессоров заказано от 0 до .
Смещение
Метод «Сдвиг» сначала копирует дерево A и перемещает каждый узел на одну позицию влево, чтобы получить дерево B. Узел, который будет расположен на -1, становится потомком процессора. .
Зеркальное отображение
«Зеркальное отображение» идеально подходит для четного числа процессоров. С помощью этого метода дерево B может быть легче построено деревом A, потому что нет никаких структурных преобразований для создания нового дерева. Кроме того, симметричный процесс упрощает этот подход. Этот метод также может обрабатывать нечетное количество процессоров, в этом случае мы можем установить процессор как корневой узел для обоих деревьев. Для остальных процессоров можно использовать «Зеркалирование».
Окраска
Нам нужно найти расписание, чтобы убедиться, что ни один процессор не должен отправлять или получать два сообщения от двух деревьев за один шаг. Ребро - это коммуникационное соединение для соединения двух узлов, и его можно пометить как 0 или 1, чтобы гарантировать, что каждый процессор может чередовать ребра, помеченные 0 и 1. Края А и B можно раскрасить в два цвета (0 и 1) так, чтобы
- ни один процессор не подключен к своим родительским узлам в А и B используя края одного цвета -
- ни один процессор не подключен к его дочерним узлам в А или же B используя края одного цвета.[7]
На каждом четном шаге ребра с 0 активируются, а ребра с 1 активируются на каждом нечетном шаге.
Сложность времени
В этом случае количество пакетов k делится пополам для каждого дерева. Оба дерева работают вместе, общее количество пакетов (верхнее дерево + нижнее дерево)
В каждом двоичном дереве отправка сообщения другим узлам занимает шагов, пока процессор не получит хотя бы один пакет в шаге . Следовательно, мы можем рассчитать все шаги как .
В результате время выполнения составляет . (Оптимальный )
Это приводит к времени выполнения .
ESBT-широковещание (связующие биномиальные деревья с непересекающимися краями)[8][9]
В этом разделе будет представлен другой алгоритм вещания с базовой моделью телефонной связи. А Гиперкуб создает сетевую систему с . Каждый узел представлен двоичным в зависимости от количества габаритов. По сути, ESBT (связующее биномиальное дерево с непересекающимися ребрами) основано на графы гиперкуба, конвейерная обработка ( сообщения делятся на пакеты) и биномиальные деревья. Процессор циклически распространяет пакеты до корней ESBT. Корни ESBT транслируют данные с биномиальным деревом. Чтобы оставить все из , шаги необходимы, потому что все пакеты распределяются . Требуется еще d шагов, пока последний листовой узел не получит пакет. В итоге шаги необходимы для трансляции сообщение через ESBT.
В результате время выполнения составляет . .
Это приводит к времени выполнения .
Смотрите также
Рекомендации
- ^ а б c Кумар, Випин (2002). Введение в параллельные вычисления (2-е изд.). Бостон, Массачусетс, США: Addison-Wesley Longman Publishing Co., Inc., стр. 185, 151, 66. ISBN 9780201648652.
- ^ а б Bruck, J .; Cypher, R .; Хо, C-T. (1992). «Трансляция множественных сообщений с обобщенными деревьями Фибоначчи». [1992] Труды четвертого симпозиума IEEE по параллельной и распределенной обработке. С. 424–431. Дои:10.1109 / SPDP.1992.242714. ISBN 0-8186-3200-3.
- ^ MPI: стандарт интерфейса передачи сообщений, версия 3.0, Форум интерфейса передачи сообщений, стр. 148, 2012
- ^ а б c Майкл Иккерт, Т. Кириц, П. Сандерс Алгоритм Парралеля - Скрипт (Немецкий), Технологический институт Карлсруэ, стр. 29-32, 2009 г.
- ^ Майкл Иккерт, Т. Кириц, П. Сандерс Алгоритм Парралеля - Скрипт (Немецкий), Технологический институт Карлсруэ, стр.33-37, 2009 г.
- ^ П. Сандерс [1] (Немецкий), Технологический институт Карлсруэ, стр. 82-96, 2018 г.
- ^ а б Сандерс, Питер; Спек, Йохен; Träff, Джеспер Ларссон (2009). «Двухдеревянные алгоритмы широковещательной передачи, сокращения и сканирования с полной полосой пропускания». Параллельные вычисления. 35 (12): 581–594. Дои:10.1016 / j.parco.2009.09.001. ISSN 0167-8191.
- ^ Майкл Иккерт, Т. Кириц, П. Сандерс Алгоритм Парралеля - Скрипт (Немецкий), Технологический институт Карлсруэ, стр. 40-42, 2009 г.
- ^ П. Сандерс [2] (Немецкий), Технологический институт Карлсруэ, стр. 101-104, 2018 г.
![{ displaystyle M [1..m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3e38b38a48f71cb8c1c43b0011a71a56a376f3b)