WikiDer > Бычий график - Википедия

Бычий график
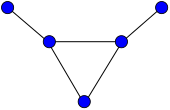График быка
Вершины	5
Края	5
Радиус	2
Диаметр	3
Обхват	3
Автоморфизмы	2 (Z/2Z)
Хроматическое число	3
Хроматический индекс	3
Характеристики	Планарный Единичное расстояние
Таблица графиков и параметров

в математический поле теория графов, то бычий график это планарный неориентированный граф с 5 вершинами и 5 ребрами, в виде треугольника с двумя непересекающимися висячими ребрами.^[1]

Она имеет хроматическое число 3, хроматический индекс 3, радиус 2, диаметр 3 и обхват 3. Это также самодополняющий граф, а блочный граф, а разделенный график, интервальный график, а граф без когтей, а 1-вершинно-связный граф и 1-реберный граф.

Графы без быков

График не имеет быков, если в нем нет быков. индуцированный подграф. В графы без треугольников графы без быков, поскольку каждый бык содержит треугольник. В сильная теорема о совершенном графе было доказано для графов без быков задолго до его доказательства для общих графов,^[2] и полиномиальное время Алгоритм распознавания идеальных графов без быков известен.^[3]

Мария Чудновская и Шмуэль Сафра изучали графы без быков в более общем плане, показывая, что любой такой граф должен иметь либо большой клика или большой независимый набор (это Гипотеза Эрдеша – Хайнала для бычьего графа),^[4] и разработка общей теории структуры этих графов.^[5][6][7]

Хроматический и характеристический полином

Три графика с хроматический полином равно ${ Displaystyle (х-2) (х-1) ^ {3} х}$.

В хроматический полином графа быков ${ Displaystyle (х-2) (х-1) ^ {3} х}$. Два других графа хроматически эквивалентны графу быка.

Его характеристический многочлен является ${ Displaystyle -x (х ^ {2} -x-3) (х ^ {2} + x-1)}$.

Его Полином Тутте является ${ displaystyle x ^ {4} + x ^ {3} + x ^ {2} y}$.

Рекомендации