WikiDer > Пакетный код исправления ошибок - Википедия
В теория кодирования, пакетные коды с исправлением ошибок использовать методы исправления пакетные ошибки, которые являются ошибками, которые возникают во многих последовательных битах, а не в битах независимо друг от друга.
Многие коды были разработаны для исправления случайные ошибки. Однако иногда каналы могут вносить ошибки, которые локализуются в коротком интервале. Такие ошибки возникают в пакете (называемом пакетные ошибки), потому что они встречаются во многих последовательных битах. Примеры пакетных ошибок можно найти в большом количестве на носителях информации. Эти ошибки могут быть вызваны физическими повреждениями, такими как царапина на диске или удар молнии в случае беспроводных каналов. Они не независимы; они имеют тенденцию к пространственной концентрации. Если один бит имеет ошибку, вероятно, что соседние биты также могут быть повреждены. Методы, используемые для исправления случайных ошибок, неэффективны для исправления пакетных ошибок.
Определения
Всплеск длины [1]
Произнесите кодовое слово передается и принимается как Тогда вектор ошибки называется всплеском длины если ненулевые компоненты ограничены последовательные компоненты. Например, это всплеск длины
Хотя этого определения достаточно, чтобы описать, что такое пакетная ошибка, большинство инструментов, разработанных для исправления пакетных ошибок, полагаются на циклические коды. Это мотивирует наше следующее определение.
Циклический всплеск длины [1]
Вектор ошибки называется циклической пакетной ошибкой длины если его ненулевые компоненты ограничены циклически последовательные компоненты. Например, рассмотренный ранее вектор ошибок , является циклическим всплеском длины , поскольку мы рассматриваем ошибку, начиная с позиции и заканчивается в позиции . Обратите внимание, что индексы на основе, то есть первый элемент находится в позиции .
В оставшейся части этой статьи мы будем использовать термин пакет для обозначения циклического пакета, если не указано иное.
Описание пакета
Часто бывает полезно иметь компактное определение пакетной ошибки, которое включает не только ее длину, но также структуру и местоположение такой ошибки. Мы определяем описание пакета как кортеж куда - образец ошибки (то есть строка символов, начинающаяся с первой ненулевой записи в шаблоне ошибки и заканчивающаяся последним ненулевым символом), и - это место в кодовом слове, где может быть найден пакет.[1]
Например, пакетное описание шаблона ошибки является . Обратите внимание, что такое описание не уникально, потому что описывает ту же пакетную ошибку. В общем, если количество ненулевых компонент в является , тогда буду иметь разные описания пакетов, каждое из которых начинается с отличной от нуля записи . Чтобы исправить проблемы, возникающие из-за неоднозначности описания всплесков с теоремой ниже, однако перед этим нам нужно сначала определение.
Определение. Количество символов в заданном шаблоне ошибки обозначается
- Теорема (Единственность описаний всплесков). Предполагать - вектор ошибок длины с двумя описаниями пакетов и . Если тогда два описания идентичны, то есть их компоненты эквивалентны.[2]
- Доказательство. Позволять быть вес молотка (или количество ненулевых записей) . потом точно описания ошибок. За нечего доказывать. Итак, мы предполагаем, что и что описания не идентичны. Мы замечаем, что каждая ненулевая запись появится в шаблоне, и поэтому компоненты не включенный в шаблон, будет формировать циклическую серию нулей, начинающуюся после последней ненулевой записи и продолжающуюся непосредственно перед первой ненулевой записью шаблона. Мы называем набор индексов, соответствующий этому прогону, нулевым прогоном. Мы сразу же замечаем, что каждое описание пакета имеет связанный с ним нулевой цикл и что каждый нулевой цикл не пересекается. Поскольку у нас есть нулевых пробегов, и каждый из них не пересекается, в сумме различные элементы во всех нулевых пробегах. С другой стороны:
- Это противоречит Таким образом, описания пакетных ошибок идентичны.
А следствие Вышеупомянутой теоремы заключается в том, что у нас не может быть двух различных описаний пакетов для пакетов длиной
Циклические коды для коррекции пакетных ошибок
Циклические коды определены следующим образом: подумайте о символы как элементы в . Теперь мы можем думать о словах как о многочленах от где отдельные символы слова соответствуют разным коэффициентам полинома. Чтобы определить циклический код, мы выбираем фиксированный многочлен, называемый порождающий полином. Кодовые слова этого циклического кода - это все полиномы, которые делятся на этот порождающий полином.
Кодовые слова - это полиномы степени . Предположим, что порождающий полином имеет степень . Полиномы степени которые делятся на результат умножения полиномами степени . У нас есть такие многочлены. Каждому из них соответствует кодовое слово. Следовательно, для циклических кодов.
Циклические коды могут обнаруживать все пакеты длиной до . Позже мы увидим, что способность любого код ограничен сверху . Циклические коды считаются оптимальными для обнаружения пакетных ошибок, поскольку они соответствуют этой верхней границе:
- Теорема (возможность коррекции циклических пакетов). Каждый циклический код с порождающим полиномом степени может обнаруживать все всплески длины
- Доказательство. Нам нужно доказать, что если вы добавите всплеск длины к кодовому слову (то есть к многочлену, который делится на ), то результат не будет кодовым словом (т.е. соответствующий многочлен не делится на ). Достаточно показать, что никакой всплеск длины делится на . Такой всплеск имеет вид , куда Следовательно, не делится на (поскольку последний имеет степень ). не делится на (В противном случае все кодовые слова начинались бы с ). Следовательно, не делится на также.
Приведенное выше доказательство предлагает простой алгоритм обнаружения / исправления пакетных ошибок в циклических кодах: задано переданное слово (т.е.полином степени ), вычислите остаток от этого слова при делении на . Если остаток равен нулю (т.е. если слово делится на ), то это действительное кодовое слово. В противном случае сообщите об ошибке. Чтобы исправить эту ошибку, вычтите этот остаток из переданного слова. Результат вычитания будет делиться на (т.е. это будет действительное кодовое слово).
По верхней границе обнаружения пакетных ошибок (), мы знаем, что циклический код не может обнаружить все всплески длины . Однако циклические коды действительно могут обнаруживать наиболее всплески длины . Причина в том, что обнаружение не удается, только если пакет делится на . Помимо двоичных алфавитов существуют всплески длины . Из них только делятся на . Поэтому вероятность неудачного обнаружения очень мала () предполагая равномерное распределение по всем всплескам длины .
Теперь мы рассмотрим фундаментальную теорему о циклических кодах, которая поможет в разработке эффективных кодов с исправлением пакетов ошибок путем разделения пакетов на разные классы смежности.
- Теорема (Отличное Cosets). Линейный код является код, исправляющий пакетные ошибки, если все пакеты ошибок имеют длину лежат в разных смежные классы из .
- Доказательство. Позволять быть отличными пакетными ошибками длины которые лежат в одном классе кода . потом это кодовое слово. Следовательно, если мы получим мы можем расшифровать его либо или же . Напротив, если все пакетные ошибки и не принадлежат к одному классу смежных классов, то каждая пакетная ошибка определяется своим синдромом. Затем ошибку можно исправить с помощью ее синдрома. Таким образом, линейный код является код, исправляющий пакетные ошибки, тогда и только тогда, когда все пакеты ошибок имеют длину лежат в разных смежных классах .
- Теорема (классификация кодовых слов пакетных ошибок). Позволять быть линейным код исправления пакетных ошибок. Тогда никакой ненулевой всплески длины может быть кодовым словом.
- Доказательство. Позволять быть кодовым словом с пакетом длины . Таким образом, он имеет образец , куда и слова длины Следовательно, слова и две очереди длины . Для двоичных линейных кодов они принадлежат одному классу смежности. Это противоречит теореме об отличных классах смежности, поэтому нет ненулевого пакета длины может быть кодовым словом.
Границы исправления пакетных ошибок
Верхние границы обнаружения и исправления пакетных ошибок
Под верхней границей мы подразумеваем предел нашей способности обнаруживать ошибки, за который мы никогда не сможем выйти. Предположим, мы хотим разработать код, который может обнаруживать все пакетные ошибки длины Естественный вопрос: дано и , какой максимум что мы никогда не сможем достичь большего? Другими словами, какова верхняя граница длины всплесков, которые мы можем обнаружить с помощью любого код? Следующая теорема дает ответ на этот вопрос.
- Теорема (возможность обнаружения пакетных ошибок). Возможность обнаружения пакетных ошибок любого код
- Доказательство. Сначала мы замечаем, что код может обнаруживать все пакеты длины тогда и только тогда, когда никакие два кодовых слова не отличаются пакетом длины . Предположим, у нас есть два кодовых слова и которые отличаются вспышкой длины . При получении , мы не можем сказать, действительно ли переданное слово без ошибок передачи, или с ошибкой пакета что произошло во время передачи. Теперь предположим, что каждые два кодовых слова отличаются более чем на пакет длины Даже если переданное кодовое слово попадает в очередь длины , оно не будет заменено другим допустимым кодовым словом. Получив его, мы можем сказать, что это взрывом Из вышеприведенного наблюдения мы знаем, что никакие два кодовых слова не могут разделять первое символы. Причина в том, что даже если они отличаются от всех остальных символы, они по-прежнему будут отличаться по длине Следовательно, количество кодовых слов удовлетворяет Применение в обе стороны и переставляя, мы видим, что .
Теперь мы повторяем тот же вопрос, но для исправления ошибок: дано и , какова верхняя граница длины всплесков, которые мы можем исправить любым код? Следующая теорема дает предварительный ответ на этот вопрос:
- Теорема (возможность пакетного исправления ошибок). Возможность пакетного исправления ошибок любого код удовлетворяет
- Доказательство. Сначала мы замечаем, что код может исправить все пакеты длины тогда и только тогда, когда никакие два кодовых слова не отличаются на сумму двух пакетов длины Предположим, что два кодовых слова и отличаться очередями и длины каждый. При получении пораженный взрывом , мы могли бы интерпретировать это так, как будто это пораженный взрывом . Мы не можем сказать, является ли переданное слово или же . Теперь предположим, что каждые два кодовых слова отличаются более чем на два пакета длины . Даже если переданное кодовое слово попадает в серию , это не будет похоже на другое кодовое слово, которое подверглось очередной вспышке. Для каждого кодового слова позволять обозначают множество всех слов, отличных от взрывом длины Заметь включает сам. Из вышеприведенного наблюдения мы знаем, что для двух разных кодовых слов и и не пересекаются. У нас есть кодовые слова. Следовательно, можно сказать, что . Кроме того, у нас есть . Подставив последнее неравенство в первое и взяв за основу логарифмируя и переставляя, получаем приведенную выше теорему.
Более сильный результат дает оценка Ригера:
- Теорема (оценка Ригера). Если способность исправления пакетных ошибок линейный блочный код, тогда .
- Доказательство. Любой линейный код, который может исправить любую последовательность пакетов длины не может быть продолжительной как кодовое слово. Если бы у него был всплеск длины в качестве кодового слова, затем последовательность длины может изменить кодовое слово на пакет длиной , которое также можно было получить, сделав пакетную ошибку длиной во всех нулевых кодовых словах. Если вначале векторы не равны нулю символов, то векторы должны быть из разных подмножеств массива, чтобы их различие не было кодовым словом пакетов длины . При выполнении этого условия количество таких подмножеств не меньше, чем количество векторов. Таким образом, количество подмножеств будет не менее . Следовательно, мы имеем как минимум различных символов, в противном случае разность двух таких многочленов была бы кодовым словом, которое представляет собой сумму двух пакетов длины Таким образом, это доказывает границу Ригера.
Определение. Линейный код с исправлением пакетов ошибок, достигающий вышеупомянутой границы Ригера, называется оптимальным кодом с исправлением пакетов ошибок.
Дополнительные ограничения на исправление пакетных ошибок
Существует более одной верхней границы достижимой кодовой скорости линейных блочных кодов для множественной фазированной пакетной коррекции (MPBC). Одна такая граница ограничена максимальной корректируемой длиной циклического пакета в каждом подблоке или, что эквивалентно, ограничением минимальной длины без ошибок или промежутка в каждом фазированном пакете. Эта граница, когда она сведена к частному случаю ограничения для одиночной пакетной коррекции, является границей Абрамсона (следствие границы Хэмминга для пакетной коррекции ошибок), когда длина циклического пакета меньше половины длины блока.[3]
- Теорема (количество всплесков). За над двоичным алфавитом есть векторы длины которые являются всплесками длины .[1]
- Доказательство. Поскольку длина пакета есть уникальное описание пакета, связанное с пакетом. Всплеск может начаться в любой из позиции выкройки. Каждый узор начинается с и содержать длину . Мы можем думать об этом как о наборе всех строк, начинающихся с и иметь длину . Таким образом, всего возможных таких шаблонов, и всего всплески длины Если мы включим пакет с нулевыми значениями, мы получим векторы, представляющие пакеты длины
- Теорема (оценка количества кодовых слов). Если двоичный код исправления пакетных ошибок имеет не более кодовые слова.
- Доказательство. С , мы знаем, что есть всплески длины . Скажите, что в коде есть кодовые слова, то есть кодовые слова, которые отличаются от кодового слова пакетом длины . Каждый из слова должны быть разными, иначе код будет иметь расстояние . Следовательно, подразумевает
- Теорема (оценки Абрамсона). Если бинарный линейный код исправления пакетных ошибок, длина его блока должна удовлетворять:
- Доказательство: Для линейного код, есть кодовые слова. По нашему предыдущему результату мы знаем, что
- Изоляция , мы получили . С и должно быть целым числом, у нас есть .
Замечание. называется избыточностью кода, и в альтернативной формулировке оценок Абрамсона
Пожарные коды[3][4][5]
Пока циклические коды в общем, являются мощными инструментами для обнаружения пакетных ошибок, теперь мы рассмотрим семейство двоичных циклических кодов под названием Fire Codes, которые обладают хорошими возможностями исправления одиночных пакетных ошибок. Одной серией, скажем, длины , мы имеем в виду, что все ошибки, которые есть в полученном кодовом слове, лежат в фиксированном диапазоне цифры.
Позволять быть неприводимый многочлен степени над , и разреши быть периодом . Период , как и любого полинома, определяется как наименьшее положительное целое число такой, что Позволять быть натуральным числом, удовлетворяющим и не делится на , куда это период . Определите пожарный кодекс следующими порождающий полином:
Мы покажем, что является код исправления пакетных ошибок.
- Лемма 1.
- Доказательство. Позволять - наибольший общий делитель двух многочленов. С неприводимо, или же . Предполагать тогда для некоторой постоянной . Но, является делителем поскольку является делителем . Но это противоречит нашему предположению, что не разделяет Таким образом, Доказательство леммы.
- Лемма 2. Если - многочлен периода , тогда если и только если
- Доказательство. Если , тогда . Таким образом,
- Теперь предположим . Потом, . Мы показываем, что делится на индукцией по . Базовый случай следует. Поэтому предположим . Мы знаем это делит оба (так как имеет период )
- Но неприводимо, поэтому он должен делить оба и ; таким образом, он также делит разность двух последних многочленов, . Тогда следует, что разделяет . Наконец, он также разделяет: . По предположению индукции , тогда .
Следствие леммы 2 состоит в том, что, поскольку есть период , тогда разделяет если и только если .
Если мы сможем показать, что все всплески длины или меньше встречаются в разных смежные классы, мы можем использовать их как лидеры смежных классов которые образуют исправимые шаблоны ошибок. Причина проста: мы знаем, что у каждого смежного класса есть уникальный расшифровка синдрома связанных с ним, и если все пакеты разной длины встречаются в разных смежных классах, то все они имеют уникальные синдромы, что облегчает исправление ошибок.
Доказательство теоремы
Позволять и быть полиномами со степенями и , представляющие собой всплески длины и соответственно с Целые числа представляют начальные позиции пакетов и меньше длины блока кода. Ради противоречия предположим, что и находятся в одном классе. Потом, является допустимым кодовым словом (поскольку оба термина находятся в одном смежном классе). Без потери общности выберите . Посредством теорема деления мы можем написать: для целых чисел и . Перепишем многочлен следующее:
Обратите внимание, что при второй манипуляции мы ввели термин . Нам разрешено это делать, поскольку пожарные коды действуют на . По нашему предположению, является допустимым кодовым словом и, следовательно, должно быть кратным . Как упоминалось ранее, поскольку факторы относительно простые, должен делиться на . Присмотревшись к последнему выражению, полученному для мы замечаем, что делится на (по следствию леммы 2). Следовательно, делится на или это . Снова применяя теорему о делении, мы видим, что существует многочлен со степенью такой, что:
Тогда мы можем написать:
Приравнивая степени обеих сторон, мы получаем С мы можем заключить что подразумевает и . Обратите внимание, что в расширении:
период, термин появляется, но поскольку , результирующее выражение не содержит , следовательно и впоследствии Это требует, чтобы , и . Мы можем дополнительно пересмотреть наше разделение к отражать то есть . Подставляя обратно в дает нам,
С , у нас есть . Но неприводимо, поэтому и должно быть относительно простым. С это кодовое слово, должен делиться на , так как не может делиться на . Следовательно, должно быть кратно . Но он также должен быть кратным , что означает, что он должен быть кратным но это именно длина блока кода. Следовательно, не может быть кратным так как они оба меньше чем . Таким образом, наше предположение о кодовое слово неверно, и поэтому и находятся в разных смежных классах, с уникальными синдромами и, следовательно, исправимы.
Пример: код пожара с исправлением ошибок из 5 пакетов
Используя теорию, представленную в предыдущем разделе, рассмотрим построение -схема исправления ошибок пожарного кода. Помните, что для построения кода огня нам нужен неприводимый многочлен. , целое число , представляющий возможность исправления пакетных ошибок нашего кода, и нам нужно удовлетворить свойство, которое не делится на период . С учетом этих требований рассмотрим неприводимый многочлен , и разреши . С примитивный многочлен, его период . Мы подтверждаем, что не делится на . Таким образом,
генератор пожарного кода. Мы можем вычислить длину блока кода, вычислив наименьшее общее кратное и . Другими словами, . Таким образом, приведенный выше код пожара представляет собой циклический код, способный исправить любой пакет длины. или менее.
Двоичные коды Рида – Соломона
Определенные семейства кодов, например Рид – Соломон, оперируйте с размером алфавита больше двоичного. Это свойство наделяет такие коды мощными возможностями исправления пакетных ошибок. Рассмотрим код, работающий с . Каждый символ алфавита может быть представлен как биты. Если является Код Рида – Соломона , мы можем думать о как код поверх .
Причина, по которой такие коды являются мощным средством исправления пакетных ошибок, заключается в том, что каждый символ представлен биты, и вообще неважно, сколько из них биты ошибочные; будь то один бит или все биты содержат ошибки, с точки зрения декодирования это все еще ошибка одного символа. Другими словами, поскольку пакетные ошибки обычно возникают в кластерах, существует большая вероятность того, что несколько двоичных ошибок вносят вклад в ошибку одного символа.
Обратите внимание, что всплеск ошибки могут повлиять самое большее символы, и взрыв может повлиять самое большее символы. Затем всплеск может повлиять самое большее символы; это означает, что -symbols-код исправления ошибок может исправить всплеск длины не более .
В целом -исправление ошибок кода Рида – Соломона по может исправить любую комбинацию
или меньшее количество длинных серий , помимо возможности исправлять -случайные ошибки наихудшего случая.
Пример двоичного кода RS
Позволять быть Код RS закончился . Этот код использовался НАСА в их Кассини-Гюйгенс космический корабль.[6] Способен исправлять ошибки символа. Теперь мы построим двоичный код RS из . Каждый символ будет записан с использованием биты. Следовательно, двоичный код RS будет иметь как его параметры. Он способен исправить любой одиночный пакет длины .
Чередующиеся коды
Перемежение используется для преобразования сверточных кодов из корректоров случайных ошибок в корректоры пакетных ошибок. Основная идея использования перемежаемых кодов состоит в том, чтобы смешивать символы в приемнике. Это приводит к рандомизации пакетов принятых ошибок, которые находятся близко друг к другу, и затем мы можем применить анализ для случайного канала. Таким образом, основная функция, выполняемая перемежителем в передатчике, заключается в изменении входной последовательности символов. В приемнике обращенный перемежитель изменит принятую последовательность, чтобы вернуть исходную неизмененную последовательность в передатчике.
Способность перемежителя корректировать пакетные ошибки
- Теорема. Если способность исправления пакетных ошибок некоторого кода то способность исправления пакетных ошибок его -way чередование
- Доказательство: Предположим, что у нас есть код, который может исправить все пакеты длины Чередование может предоставить нам код, который может исправить все пакеты длины для любого данного . Если мы хотим закодировать сообщение произвольной длины с помощью чередования, сначала мы делим его на блоки длиной . Мы пишем записи каждого блока в матрица с использованием строкового порядка. Затем мы кодируем каждую строку, используя код. Мы получим матрица. Теперь эта матрица считывается и передается в порядке столбца. Хитрость в том, что если происходит всплеск длины в передаваемом слове, то каждая строка будет содержать примерно последовательные ошибки (точнее, каждая строка будет содержать пакет длиной не менее и самое большее ). Если тогда и код может исправить каждую строку. Следовательно, чередующиеся код может исправить всплеск длины . Наоборот, если тогда хотя бы одна строка будет содержать более последовательные ошибки, и код может не исправить их. Следовательно, исправляющая способность перемежающихся код точно Эффективность BEC перемеженного кода остается такой же, как и у оригинального. код. Это правда, потому что:
Блочный перемежитель
На рисунке ниже показан перемежитель 4 на 3.
Вышеупомянутый перемежитель называется блочный перемежитель. Здесь входные символы записываются последовательно в строках, а выходные символы получаются путем последовательного чтения столбцов. Таким образом, это в виде множество. В общем, - длина кодового слова.
Емкость блочного перемежителя: Для блочный перемежитель и пакет длины верхний предел количества ошибок Это очевидно из того факта, что мы читаем выходной столбец, а количество строк равно . По теореме выше для корректирующей способности до максимальная допустимая длина пакета составляет Для длины серии , декодер может выйти из строя.
Эффективность блочного перемежителя (): Это определяется путем определения отношения длины пакета, при котором декодер может выйти из строя, к памяти перемежителя. Таким образом, мы можем сформулировать в качестве
Недостатки блочного перемежителя: Как видно из рисунка, столбцы читаются последовательно, получатель может интерпретировать одну строку только после того, как получит полное сообщение, а не до этого. Кроме того, получателю требуется значительный объем памяти для хранения принятых символов и он должен хранить все сообщение. Таким образом, эти факторы вызывают два недостатка: один - это задержка, а другой - хранилище (довольно большой объем памяти). Этих недостатков можно избежать, используя описанный ниже сверточный перемежитель.
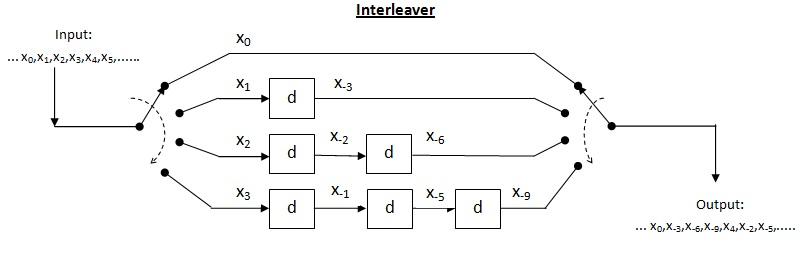
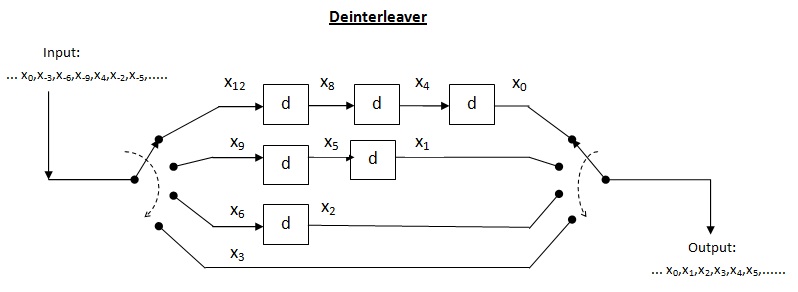
Сверточный перемежитель
Перекрестный перемежитель - это разновидность системы мультиплексор-демультиплексор. В этой системе используются линии задержки для постепенного увеличения длины. Линия задержки - это в основном электронная схема, используемая для задержки сигнала на определенное время. Позволять быть количеством линий задержки и - количество символов, вводимых каждой линией задержки. Таким образом, разделение между последовательными входами = символы. Пусть длина кодового слова Таким образом, каждый символ во входном кодовом слове будет на отдельной линии задержки. Пусть пакетная ошибка длины происходить. Поскольку разделение между последовательными символами равно количество ошибок, которые могут содержаться в выводе с деинтерлиброванием, равно По приведенной выше теореме для исправления ошибок до , максимальная допустимая длина пакета составляет Для длины серии декодер может выйти из строя.
Эффективность перекрестного перемежителя (): Его можно найти, взяв отношение длины пакета, где декодер может выйти из строя, к памяти перемежителя. В этом случае память перемежителя может быть рассчитана как
Таким образом, мы можем сформулировать следующее:
Производительность перекрестного перемежителя: Как показано на приведенном выше рисунке перемежителя, вывод - это не что иное, как диагональные символы, генерируемые в конце каждой линии задержки. В этом случае, когда переключатель входного мультиплексора завершается примерно наполовину, мы можем прочитать первую строку на приемнике. Таким образом, нам нужно сохранить максимум около половины сообщения у получателя, чтобы прочитать первую строку. Это резко снижает вдвое потребность в хранилище. Поскольку теперь для чтения первой строки требуется только половина сообщения, задержка также уменьшается вдвое, что является хорошим улучшением по сравнению с блочным перемежителем. Таким образом, вся память перемежителя делится между передатчиком и приемником.
Приложения
Компакт-диск
Без кодов исправления ошибок цифровое аудио было бы технически невозможно.[7] В Коды Рида – Соломона может исправить поврежденный символ с помощью единственной битовой ошибки так же легко, как он может исправить символ со всеми ошибочными битами. Это делает коды RS особенно подходящими для исправления пакетных ошибок.[5] Безусловно, наиболее распространенное применение кодов RS - компакт-диски. В дополнение к базовому исправлению ошибок, обеспечиваемому кодами RS, защиту от пакетных ошибок из-за царапин на диске обеспечивает перекрестный перемежитель.[3]
Современная цифровая аудиосистема на компакт-дисках была разработана N.V. Philips из Нидерландов и Sony Corporation из Японии (соглашение подписано в 1979 г.).
Компакт-диск представляет собой алюминированный диск диаметром 120 мм, покрытый прозрачным пластиковым покрытием, со спиральной дорожкой длиной примерно 5 км, которая оптически сканируется лазером с длиной волны ~ 0,8 мкм с постоянной скоростью ~ 1,25 м / с. Для достижения этой постоянной скорости вращение диска варьируется от ~ 8 об / с при сканировании на внутренней части дорожки до ~ 3,5 об / с на внешней части. Ямки и уступы представляют собой углубления (глубиной 0,12 мкм) и плоские сегменты, составляющие двоичные данные вдоль дорожки (шириной 0,6 мкм).[8]
Процесс компакт-диска можно абстрагировать как последовательность следующих подпроцессов: -> Канальное кодирование источника сигналов -> Механические подпроцессы подготовки мастер-диска, создания пользовательских дисков и распознавания сигналов, встроенных в пользовательские диски во время воспроизведения - канал-> Декодирование сигналов, воспринимаемых с пользовательских дисков
Процесс подвержен как пакетным ошибкам, так и случайным ошибкам.[7] К ошибкам разрыва относятся те, которые возникают из-за материала диска (дефекты алюминиевой отражающей пленки, плохой коэффициент отражения прозрачного материала диска), изготовления диска (дефекты во время формования и резки диска и т. направление записи) и варианты механизма воспроизведения. К случайным ошибкам относятся ошибки, вызванные дрожанием восстановленной сигнальной волны и помехами в сигнале. CIRC (Перемежающийся код Рида – Соломона) является основой для обнаружения и исправления ошибок в процессе CD. Он последовательно исправляет пакеты ошибок длиной до 3500 бит (длина 2,4 мм, как видно на поверхности компакт-диска) и компенсирует пакеты ошибок размером до 12000 бит (8,5 мм), которые могут быть вызваны незначительными царапинами.
Кодировка: Звуковые волны дискретизируются и преобразуются в цифровую форму аналого-цифровым преобразователем. Звуковая волна дискретизируется по амплитуде (44,1 кГц или 44 100 пар, по одной для левого и правого каналов стереозвука). Амплитуде в экземпляре назначается двоичная строка длиной 16. Таким образом, каждая выборка создает два двоичных вектора из или 4 байты данных. Каждая секунда записанного звука дает 44 100 × 32 = 1411 200 бит (176 400 байт) данных.[5] Поток дискретизированных данных 1,41 Мбит / с проходит через систему исправления ошибок, в конечном итоге преобразуясь в поток 1,88 Мбит / с.
Вход для кодировщика состоит из входных кадров, каждый из которых состоит из 24 8-битных символов (12 16-битных отсчетов от аналого-цифрового преобразователя, по 6 от левого и правого источников данных (звука)). Кадр может быть представлен как куда и байты из левого и правого каналов из образец рамы.
Первоначально байты переставляются для формирования новых кадров, представленных куда представлять левый и правый отсчеты из кадра после двух промежуточных кадров.
Затем эти 24 символа сообщения кодируются с использованием кода Рида – Соломона C2 (28,24,5), который является сокращенным кодом RS по сравнению с . Это исправление двух ошибок, минимальное расстояние 5. Это добавляет 4 байта избыточности, формирование нового кадра: . Результирующее кодовое слово из 28 символов проходит через перекрестный перемежитель (28,4), что приводит к 28 перемеженным символам. Затем они проходят через код С1 (32,28,5) RS, в результате чего образуются кодовые слова из 32 закодированных выходных символов. Дальнейшая перегруппировка нечетных пронумерованных символов кодового слова с четными пронумерованными символами следующего кодового слова выполняется, чтобы разбить любые короткие пакеты, которые могут все еще присутствовать после вышеупомянутого перемежения с задержкой на 4 кадра. Таким образом, на каждые 24 входных символа будет 32 выходных символа, дающих . Наконец, добавляется один байт управляющей и отображаемой информации.[5] Затем каждый из 33 байтов преобразуется в 17 бит с помощью EFM (от восьми до четырнадцати модуляции) и добавления 3 битов слияния. Таким образом, кадр из шести выборок дает 33 байта × 17 бит (561 бит), к которым добавляются 24 бита синхронизации и 3 бита слияния, что в сумме дает 588 бит.
Расшифровка: Проигрыватель компакт-дисков (декодер CIRC) принимает поток данных из 32 выходных символов. Этот поток сначала проходит через декодер D1. Отдельные разработчики систем компакт-дисков должны выбирать методы декодирования и оптимизировать характеристики своих продуктов. Находятся на минимальном расстоянии 5 Каждый из декодеров D1, D2 может корректировать комбинацию ошибки и стирания такие, что .[5] В большинстве решений декодирования D1 предназначен для исправления одиночной ошибки. А в случае более 1 ошибки этот декодер выдает 28 стираний. Деинтерлейвер на следующем этапе распределяет эти стирания по 28 кодовым словам D2. Опять же, в большинстве решений D2 настроен только на стирание (более простое и менее дорогое решение). Если встретится более 4 стираний, D2 выводит 24 стирания. После этого система маскирования ошибок пытается интерполировать (по соседним символам) в случае неисправимых символов, при этом звуки, соответствующие таким ошибочным символам, приглушаются.
Производительность CIRC:[7] CIRC скрывает длинные ошибки перебора простой линейной интерполяцией. Длина дорожки 2,5 мм (4000 бит) - это максимальная длина пакета, которую можно полностью исправить. Длина дорожки 7,7 мм (12300 бит) - это максимальная длина пакета, которую можно интерполировать. Частота интерполяции выборки - одна каждые 10 часов при частоте ошибок по битам (BER). и 1000 выборок в минуту при BER = Образцы необнаруживаемых ошибок (клики): менее одной каждые 750 часов при BER = и пренебрежимо мала при BER = .
Смотрите также
- Обнаружение и исправление ошибок
- Коды исправления ошибок с обратной связью
- Скорость кода
- Исправление ошибок Рида – Соломона
Рекомендации
- ^ а б c d Границы кодирования для кодов многократной пакетной коррекции и кодов одиночной пакетной коррекции
- ^ Теория информации и кодирования: студенческое издание, Р. Дж. МакЭлис
- ^ а б c Лин, Сан и Чаопин Син. Теория кодирования: первый курс. Кембридж, Великобритания: Cambridge UP, 2004. Печать
- ^ а б Мун, Тодд К. Кодирование с исправлением ошибок: математические методы и алгоритмы. Хобокен, Нью-Джерси: Wiley-Interscience, 2005. Печать
- ^ а б c d е ж Лин, Шу и Даниэль Дж. Костелло. Кодирование с контролем ошибок: основы и приложения. Река Аппер Сэдл, штат Нью-Джерси: Pearson-Prentice Hall, 2004. Печать
- ^ http://quest.arc.nasa.gov/saturn/qa/cassini/Error_correction.txt В архиве 2012-06-27 на Wayback Machine
- ^ а б c Коды контроля алгебраических ошибок (осень 2012 г.) - Раздаточные материалы Стэнфордского университета
- ^ МакЭлис, Роберт Дж. Теория информации и кодирования: математическая основа коммуникации. Ридинг, Массачусетс: издательство Addison-Wesley Pub., Advanced Book Program, 1977 г. Печать














































































































































































































![{ displaystyle [мин, мк] _ {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/479cc66e2a601a8f28c80c0d3136e9d45f84728d)










![{ displaystyle [255,223,33]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc05fee57b496252bf9064f1e35606fae8d805dc)




![{ displaystyle [2040,1784,33] _ {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0de5be730230c649eac90e01bb084dbcd81319a)