WikiDer > Уравнение Батлера – Фольмера
В электрохимия, то Уравнение Батлера – Фольмера (названный в честь Джон Альфред Валентайн Батлер[1] и Макс Волмер), также известный как Эрдей-Груз–Фольмер уравнение, является одним из самых фундаментальных соотношений в электрохимическая кинетика. Он описывает, как электрический ток через электрод зависит от разницы напряжений между электродом и объемным электролитом для простой мономолекулярной окислительно-восстановительной реакции, учитывая, что оба катодный и анодный реакция происходит на том же электрод:[2]
Уравнение Батлера-Фольмера
Уравнение Батлера – Фольмера:
или в более компактной форме:
куда:
- : электрод плотность тока, Являюсь2 (определяется как j = I / S)
- : плотность тока обмена, Являюсь2
- : электродный потенциал, V
- : равновесный потенциал, В
- : абсолютная температура, К
- : количество электронов, участвующих в электродной реакции
- : Постоянная Фарадея
- : универсальная газовая постоянная
- : так называемый катодный коэффициент передачи заряда, безразмерный
- : так называемый коэффициент анодного переноса заряда, безразмерный
- : активация перенапряжение (определяется как ).
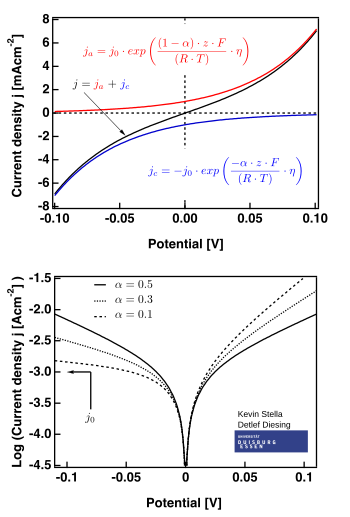
На правом рисунке показаны графики, действительные для .
Предельные случаи
Есть два предельные случаи уравнения Батлера – Фольмера:
- область низкого перенапряжения (называемая «поляризационным сопротивлением», т.е. когда E ≈ Eэкв), где уравнение Батлера – Фольмера упрощается до:
- ;
- область высокого перенапряжения, где уравнение Батлера – Фольмера упрощается до Уравнение Тафеля. Когда , первый член доминирует, а когда , второй член доминирует.
- для катодной реакции, когда E << Eэкв, или же
- для анодной реакции, когда E >> Eэкв
куда и являются константами (для данной реакции и температуры) и называются константами уравнения Тафеля. Теоретические значения констант уравнения Тафеля различны для катодного и анодного процессов. Однако склон Тафеля можно определить как:
куда это фарадеевское течение, выражаемое как , существование и катодный и анодный парциальные токи соответственно.
Расширенное уравнение Батлера-Фольмера
Более общая форма уравнения Батлера – Фольмера, применимая к условиям, связанным с массопереносом, может быть записана как:[3]
куда:
- j - плотность тока, А / м2,
- cо и cр относятся к концентрации окисляемых и восстанавливаемых веществ, соответственно,
- c (0, t) - зависящая от времени концентрация на нулевом расстоянии от поверхности электрода.
Вышеупомянутая форма упрощается до обычной (показанной в верхней части изделия), когда концентрация электроактивных частиц на поверхности равна концентрации в массе.
Есть две скорости, которые определяют отношение тока к напряжению для электрода. Во-первых, это скорость химической реакции на электроде, которая потребляет реагенты и производит продукты. Это известно как перенос заряда ставка. Второй - это скорость подачи реагентов и удаления продуктов из области электрода с помощью различных процессов, включая диффузию, миграцию и конвекцию. Последний известен как массообмен ставка[Примечание 1]. Эти две скорости определяют концентрации реагентов и продуктов на электроде, которые, в свою очередь, определяются ими. Самая низкая из этих скоростей будет определять общую скорость процесса.
Простое уравнение Батлера – Фольмера предполагает, что концентрации на электроде практически равны концентрациям в объеме электролита, что позволяет выразить ток только как функцию потенциала. Другими словами, предполагается, что скорость массопереноса намного больше, чем скорость реакции, и что в реакции преобладает более медленная скорость химической реакции. Несмотря на это ограничение, применение уравнения Батлера – Фольмера в электрохимии очень велико, и его часто считают «центральным в феноменологической кинетике электрода».[4]
Расширенное уравнение Батлера – Фольмера не делает этого предположения, а скорее принимает концентрации на электроде как заданные, давая соотношение, в котором ток выражается как функция не только потенциала, но и заданных концентраций. Скорость массообмена может быть относительно небольшой, но ее влияние на химическую реакцию проявляется только через измененные (заданные) концентрации. Фактически, концентрации также являются функцией потенциала. Полная обработка, которая дает ток как функцию только потенциала, будет выражена расширенным уравнением Батлера – Фольмера, но потребует явного включения эффектов массопереноса, чтобы выразить концентрации как функции потенциала.
Вывод
Общее выражение
Следующий вывод расширенного уравнения Батлера – Фольмера адаптирован из вывода Барда и Фолкнера.[3] и Ньюман и Томас-Алая.[5] Для простого мономолекулярного одношагового реакция формы:
- O + ne− → R
Вперед и назад скорость реакции (vж и vб) и из Законы электролиза Фарадея, соответствующие плотности электрического тока (j), можно записать как:
куда kж и kб являются константы скорости реакции, с единицами измерения частоты (1 / время) и cо и cр - поверхностные концентрации (моль / площадь) окисленных и восстановленных молекул соответственно (записанные как cо(0, t) и cр(0, t) в предыдущем разделе). Чистая скорость реакции v и чистая плотность тока j тогда:[Заметка 2]
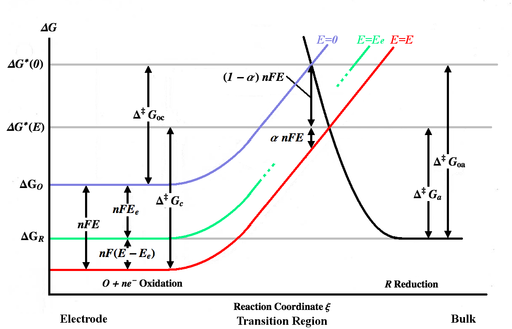
На рисунке выше показаны различные Энергия Гиббса кривые как функция координата реакции ξ. Координата реакции - это примерно мера расстояния, при этом корпус электрода находится слева, а основная масса раствора - справа. Синяя кривая энергии показывает увеличение энергии Гиббса для окисленной молекулы по мере того, как она приближается к поверхности электрода, когда не применяется потенциал. Черная кривая энергии показывает увеличение энергии Гиббса по мере приближения восстановленной молекулы к электроду. Две кривые энергии пересекаются в . Применение потенциала E к электроду сдвинет энергетическую кривую вниз[Заметка 3] (к красной кривой) nFE и точка пересечения переместится в . и - энергии активации (энергетические барьеры), которые должны преодолеть окисленные и восстановленные частицы соответственно для общего E, пока и - энергии активации для E = 0. [Примечание 4]
Предположим, что константы скорости хорошо аппроксимируются Уравнение Аррениуса,
где Аж и Аб такие константы, что Аж cо = Аб cр "правильно ориентированный" ИЛИ ЖЕ частота столкновений, а экспоненциальный член (фактор Больцмана) - это часть столкновений с достаточной энергией для преодоления барьера и реакции.
Предполагая, что энергетические кривые в переходной области практически линейны, они могут быть представлены там как:
(синяя кривая) (красная кривая) (черная кривая)
В коэффициент передачи заряда для этого простого случая эквивалентен фактору симметрии и может быть выражен через наклон энергетических кривых:
Следует, что:
Для краткости определите:
Константы скорости теперь могут быть выражены как:
где константы скорости при нулевом потенциале равны:
Плотность тока j как функция приложенного потенциала E теперь можно написать:[5]:§ 8.3
Выражение через равновесный потенциал
При определенном напряжении Eе, равновесие будет достигнуто, а прямые и обратные ставки (vж и vб) будут равны. Это показано зеленой кривой на рисунке выше. Константы равновесной скорости запишем в виде kfe и kбыть, а равновесные концентрации запишем cэ и cповторно. Равновесные токи (jce и jае) будут равны и записываются как jо, который известен как плотность тока обмена.
Обратите внимание, что плотность чистого тока в состоянии равновесия будет равна нулю. Тогда константы равновесной скорости равны:
Решение вышеуказанного для kfo и kбо в терминах равновесных концентраций cэ и cповторно и плотность тока обмена jо, плотность тока j как функция приложенного потенциала E теперь можно написать:[5]:§ 8.3
Предполагая, что в объеме раствора имеет место равновесие с концентрациями и , следует, что и , а приведенное выше выражение для плотности тока j тогда уравнение Батлера – Фольмера. Обратите внимание, что E-Eе также известен как η, активация перенапряжение.
Выражение в терминах формального потенциала
Для простой реакции изменение энергии Гиббса равно:[Примечание 5]
куда аэ и аповторно являются виды деятельности в состоянии равновесия. Деятельность а связаны с концентрациями c к а = γc где γ - коэффициент активности. Равновесный потенциал задается Уравнение Нернста:
куда это стандартный потенциал
Определение формальный потенциал:[3]:§ 2.1.6
тогда равновесный потенциал равен:
Подставляя этот равновесный потенциал в уравнение Батлера – Фольмера, получаем:
который также может быть записан в терминах стандартная константа скорости kо в качестве:[3]:§ 3.3.2
Стандартная константа скорости является важным показателем поведения электрода, независимо от концентраций. Это мера скорости, с которой система приближается к равновесию. В пределе как электрод становится идеальный поляризуемый электрод и будет вести себя электрически как разомкнутая цепь (без учета емкости). Для почти идеальных электродов с малым kонеобходимы большие изменения перенапряжения для создания значительного тока. В пределе как электрод становится идеальный неполяризуемый электрод и будет вести себя как короткое замыкание. Для почти идеальных электродов с большим kонебольшие изменения перенапряжения вызовут большие изменения тока.
Смотрите также
Примечания
- ^ Например, если скорость массопереноса обусловлена только диффузией, существует максимальная скорость, с которой реагенты могут подаваться на электрод, и, следовательно, максимально возможный ток, известный как ограничивающий ток. Предельный ток, когда электродный процесс сильно массообмен контролируемый, значение плотности тока составляет:
- Dэфф эффективный коэффициент диффузии (принимая извилистость во внимание, если есть);
- δ - толщина диффузионного слоя;
- c* - концентрация электроактивных (лимитирующих) частиц в объеме электролита.
- ^ Бард[3] выбирает текущую пропорциональную чистой форвардной ставке, но выбирает потенциальную E быть электродом за вычетом электролита, который имеет сбивающий с толку (но не противоречивый) эффект получения положительного тока для отрицательного потенциала. Конвенция Ньюмана[5] в котором ток выбирается пропорционально чистой обратной скорости, используется здесь, чтобы соответствовать результатам вышеуказанных разделов.
- ^ Повышение потенциала ионов с нуля до E увеличит их к куда - заряд на ионах (см. электрохимический потенциал). Увеличение потенциала электрода уменьшит потенциал ионов вблизи электрода относительно электрода, тем самым уменьшив их .
- ^ Кривая восстановительной энергии (черная) может зависеть от потенциала, но на выводы это не влияет, пока сумма смещений окислительной и восстановительной кривых равна nFE [5]
- ^ Отметим, что изменение энергии Гиббса также равно
Рекомендации
- ^ Mayneord, W. V. (1979). "Джон Альфред Валентайн Батлер, 14 февраля 1899 г. - 16 июля 1977 г. ". Биографические воспоминания членов Королевского общества. 25: 144–178. Дои:10.1098 / rsbm.1979.0004. PMID 11615791. S2CID 1412298.
- ^ Адлер, С. (2016). «Глава 11: Источники поляризационных потерь ячеек и электродов в ТОТЭ». В Кендалле, Кевин; Кендалл, Микаэла (ред.). Высокотемпературные твердооксидные топливные элементы для 21 века (2-е изд.). Академическая пресса. Дои:10.1016 / C2011-0-09278-5. ISBN 9780124104532.
- ^ а б c d е Бард, Аллен; Фолкнер, Ларри (2001). Электрохимические методы. Основы и приложения (2-е изд.). Хобокен, Нью-Джерси: John Wiley & Sons, Inc. ISBN 978-0-471-04372-0.
- ^ J. O'M. Бокрис, А.К.Н. Редди и М. Гамбоа-Альдеко, «Современная электрохимия 2А. Основы электродики», второе издание, Kluwer Academic / Plenum Publishers, стр.1083, 2000.
- ^ а б c d е Ньюман, Джон; Thomas-Alyea, Карен Э. (2004). Электрохимические системы (3-е изд.). Хобокен, Нью-Джерси: John Wiley & Sons, Inc. ISBN 0-471-47756-7.
внешняя ссылка
 СМИ, связанные с Уравнение Батлера-Фольмера в Wikimedia Commons
СМИ, связанные с Уравнение Батлера-Фольмера в Wikimedia Commons
![{ displaystyle j = j_ {0} cdot left { exp left [{ frac { alpha _ { rm {a}} zF} {RT}} (E-E _ { rm {eq} }) right] - exp left [- { frac { alpha _ { rm {c}} zF} {RT}} (E-E _ { rm {eq}}) right] right }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f04ada917b1e46ab7d26da3300b2f080d9fd591a)
![{ displaystyle j = j_ {0} cdot left { exp left [{ frac { alpha _ {a} zF eta} {RT}} right] - exp left [- { frac { alpha _ {c} zF eta} {RT}} right] right }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90c978bf8f380997d326539e24955e0ba8bd3123)

























![{ Displaystyle J = J_ {0} left {{ frac {c _ { rm {o}} (0, t)} {c _ { rm {o}} ^ {*}}} exp left [{ frac { alpha _ { rm {a}} zF eta} {RT}} right] - { frac {c _ { rm {r}} (0, t)} {c _ { rm {r}} ^ {*}}} exp left [- { frac { alpha _ { rm {c}} zF eta} {RT}} right] right }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ba8cdc412ace94d2b8bd614a0c34bf817cca666)









![{ displaystyle k_ {f} = A_ {f} exp [- Delta ^ { ddagger} G_ {c} / RT]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6665dbea2e1416b14eb890d7a632af7a69489c4c)
![{ displaystyle k_ {b} = A_ {b} exp [- Delta ^ { ddagger} G_ {a} / RT]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b67f5c14cbc2f6dfa84ecae9c8c4cf62dfd96a9)





































