WikiDer > Центральность
| Сетевая наука | ||||
|---|---|---|---|---|
| Типы сетей | ||||
| Графики | ||||
| ||||
| Модели | ||||
| ||||
| ||||
В теория графов и сетевой анализ, показатели центральность определить наиболее важные вершины внутри графика. Приложения включают определение наиболее влиятельных людей в социальная сеть, ключевые узлы инфраструктуры в Интернет или же городские сети, и суперразбрасыватели болезни. Концепции центральности были впервые разработаны в анализ социальных сетей, и многие термины, используемые для измерения центральности, отражают их социологический источник.[1]Их не следует путать с метрики влияния узла, которые стремятся количественно оценить влияние каждого узла в сети.
Определение и характеристика показателей центральности
Индексы центральности - это ответы на вопрос "Что характеризует важную вершину?" Ответ дается в терминах функции с действительными значениями на вершинах графа, где полученные значения должны обеспечивать ранжирование, которое идентифицирует наиболее важные узлы.[2][3][4]
Слово «важность» имеет множество значений, что приводит к множеству различных определений центральности. Были предложены две схемы категоризации. «Важность» может пониматься по отношению к типу потока или передачи по сети. Это позволяет классифицировать центральные органы по типу потока, который они считают важным.[3] «Важность» можно также рассматривать как участие в целостности сети. Это позволяет классифицировать центральные элементы на основе того, как они измеряют связность.[5] Оба этих подхода разделяют центральное положение на отдельные категории. Еще один вывод состоит в том, что центральное положение, подходящее для одной категории, часто «ошибается», когда применяется к другой категории.[3]
Когда центральные элементы классифицируются по их подходу к сплоченности, становится очевидным, что большинство центральных элементов относятся к одной категории. Подсчет количества прогулок, начиная с данной вершины, отличается только способом определения и подсчета прогулок. Ограничение рассмотрения этой группой позволяет получить мягкую характеристику, которая помещает центральности в спектр из блужданий длины один (степень центральности) к бесконечным прогулкам (центральность собственных значений).[2][6] Наблюдение за тем, что многие центральные лица разделяют эти семейные отношения, возможно, объясняет высокую ранговую корреляцию между этими показателями.
Характеристика по сетевым потокам
Сеть можно рассматривать как описание путей, по которым что-то течет. Это позволяет характеризовать на основе типа потока и типа пути, закодированного центральностью. Поток может быть основан на передаче, где каждый неделимый элемент переходит от одного узла к другому, как доставка пакета от места доставки до дома клиента. Второй случай - это серийное дублирование, при котором элемент реплицируется так, что он есть как у источника, так и у цели. Примером может служить распространение информации через сплетни, при этом информация распространяется конфиденциальным образом, и как источник, так и целевой узел информируются в конце процесса. Последний случай - это параллельное дублирование, когда элемент дублируется на несколько ссылок одновременно, как радиопередача, которая предоставляет одну и ту же информацию нескольким слушателям одновременно.[3]
Точно так же тип пути может быть ограничен геодезические (кратчайшие пути), пути (ни одна вершина не посещается более одного раза), тропы (вершины можно посещать несколько раз, ни одно ребро не проходит более одного раза), или прогулки (вершины и ребра можно посещать / обходить несколько раз).[3]
Характеристика по структуре прогулки
Альтернативная классификация может быть выведена из того, как построена центральность. Это снова делится на два класса. Центральные места либо радиальный или же медиальный. Радиальные центральности подсчитывают прогулки, которые начинаются / заканчиваются в данной вершине. В степень и собственное значение центральности являются примерами радиальных центральностей, считая количество блужданий длиной один или бесконечностью. Средние центральности учитывают прогулки, которые проходят через данную вершину. Каноническим примером является посредственность центральность, количество кратчайших путей, которые проходят через данную вершину.[5]
Точно так же подсчет может фиксировать либо объем или длина прогулок. Объем - это общее количество прогулок данного типа. В эту категорию попадают три примера из предыдущего абзаца. Длина фиксирует расстояние от заданной вершины до остальных вершин в графе. Freeman's близость центральность, полное геодезическое расстояние от данной вершины до всех остальных вершин, является наиболее известным примером.[5] Обратите внимание, что эта классификация не зависит от типа подсчитываемой прогулки (например, прогулка, тропа, тропа, геодезическая).
Боргатти и Эверетт предполагают, что эта типология дает представление о том, как лучше всего сравнивать меры центральности. Центральности, помещенные в один блок в этой классификации 2 × 2, достаточно похожи, чтобы сделать правдоподобные альтернативы; можно разумно сравнить, что лучше для данного приложения. Однако показатели из разных ящиков категорически различны. Любая оценка относительной пригодности может происходить только в контексте предварительного определения, какая категория более применима, что делает сравнение спорным.[5]
Центральности радиального объема существуют на спектре
Характеристика с помощью структуры обхода показывает, что почти все широко используемые центральные элементы являются мерой радиального объема. Они кодируют убеждение, что центральность вершины является функцией центральности вершин, с которыми она связана. Центральности различаются по определению ассоциации.
Боначич показал, что если ассоциация определяется в терминах прогулки, то семейство центральностей может быть определено на основе рассматриваемой длины прогулки.[2] Центральность степени считает прогулки первой длины, а центральность собственных значений считает прогулки длиной до бесконечности. Разумны и альтернативные определения ассоциации. Альфа-центральность позволяет вершинам иметь внешний источник влияния. Центральность подграфа Эстрады предполагает подсчет только замкнутых путей (треугольников, квадратов и т. Д.).
В основе таких мер лежит наблюдение, что степени матрицы смежности графа дают количество прогулок длины, заданной этой степенью. Точно так же матричная экспонента также тесно связана с количеством прогулок заданной длины. Первоначальное преобразование матрицы смежности позволяет по-другому определить тип подсчитываемого обхода. При любом подходе центральность вершины может быть выражена как бесконечная сумма, либо
для матричных степеней или
для матричных экспонент, где
- длина прогулки,
- - преобразованная матрица смежности, а
- - параметр скидки, обеспечивающий сходимость суммы.
Семейство мер Бонацича не преобразует матрицу смежности. Альфа-центральность заменяет матрицу смежности ее противовоспалительное средство. Центральность подграфа заменяет матрицу смежности ее следом. Поразительный вывод состоит в том, что независимо от первоначального преобразования матрицы смежности все такие подходы имеют общее ограничивающее поведение. В качестве стремится к нулю, индексы сходятся к степень центральности. В качестве приближается к своему максимальному значению, показатели сходятся к центральность собственных значений.[6]
Теоретико-игровая центральность
Общей чертой большинства вышеупомянутых стандартных мер является то, что они оценивают важность узла, сосредотачиваясь только на той роли, которую узел играет сам по себе. Однако во многих приложениях такой подход неадекватен из-за синергии, которая может возникнуть, если работа узлов рассматривается в группах.
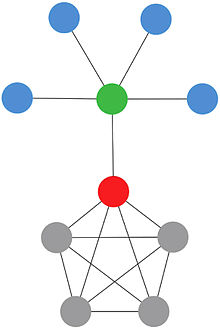
Например, рассмотрим проблему остановки эпидемии. Глядя на изображение сети выше, какие узлы мы должны вакцинировать? Основываясь на ранее описанных мерах, мы хотим распознать узлы, которые являются наиболее важными для распространения болезни. Подходы, основанные только на центральных позициях, которые сосредоточены на индивидуальных особенностях узлов, могут быть не очень хорошей идеей. Узлы в красном квадрате по отдельности не могут остановить распространение болезни, но, рассматривая их как группу, мы ясно видим, что они могут остановить болезнь, если она началась в узлах. , , и . Теоретико-игровые центры пытаются проконсультироваться с описанными проблемами и возможностями, используя инструменты теории игр. Подход, предложенный в [7] использует Значение Шепли. Из-за сложности вычисления значения Шепли по времени, большая часть усилий в этой области направляется на реализацию новых алгоритмов и методов, которые основываются на особой топологии сети или особом характере проблемы. Такой подход может привести к уменьшению временной сложности с экспоненциальной до полиномиальной.
Точно так же концепция решения распределение полномочий ([8]) применяет Индекс силы Шепли-Шубика, а не Значение Шепли, чтобы измерить двустороннее прямое влияние между игроками. Распределение действительно является типом центрированности векторов. Он используется для сортировки больших объектов данных в Hu (2020),[9] например, рейтинг колледжей США.
Важные ограничения
У индексов центральности есть два важных ограничения: одно очевидное, а другое неуловимое. Очевидным ограничением является то, что центральность, оптимальная для одного приложения, часто неоптимальна для другого приложения. В самом деле, если бы это было не так, нам не понадобилось бы столько разных центров. Иллюстрацией этого феномена является Кайт-граф Кракхардта, для которого три разных понятия центральности дают три разных выбора самой центральной вершины.[10]
Более тонкое ограничение - это широко распространенное заблуждение, что центральность вершин указывает на относительную важность вершин. Индексы центральности явно предназначены для ранжирования, позволяющего указать наиболее важные вершины.[2][3] Они хорошо справляются с этим при только что отмеченном ограничении. Они не предназначены для измерения влияния узлов в целом. В последнее время сетевые физики начали разработку метрики влияния узла для решения этой проблемы.
Ошибка двоякая. Во-первых, при ранжировании вершины упорядочиваются только по важности, а не количественно разница в важности между различными уровнями ранжирования. Это можно уменьшить, применив Централизация Фримена к рассматриваемой мере центральности, которые дают некоторое представление о важности узлов в зависимости от различий их оценок централизации. Кроме того, централизация Freeman позволяет сравнивать несколько сетей, сравнивая их наивысшие оценки централизации.[11] Однако такой подход редко используется на практике.[нужна цитата]
Во-вторых, функции, которые (правильно) идентифицируют наиболее важные вершины в данной сети / приложении, не обязательно распространяются на остальные вершины. Для большинства других сетевых узлов рейтинг может быть бессмысленным.[12][13][14][15] Это объясняет, почему, например, только первые несколько результатов поиска изображений Google появляются в разумном порядке. Рейтинг страницы - это очень нестабильный показатель, показывающий частые изменения ранга после небольших корректировок параметра перехода.[16]
Хотя невозможность обобщения индексов центральности на остальную сеть на первый взгляд может показаться нелогичным, это прямо следует из приведенных выше определений. Сложные сети имеют неоднородную топологию. В той степени, в которой оптимальная мера зависит от сетевой структуры наиболее важных вершин, мера, оптимальная для таких вершин, является субоптимальной для остальной части сети.[12]
Центральность степени

Исторически первым и концептуально самым простым является степень центральности, который определяется как количество связей, связанных с узлом (т. е. количество связей, которые имеет узел). Степень может быть интерпретирована с точки зрения непосредственного риска узла для перехвата всего, что проходит через сеть (например, вируса или некоторой информации). В случае направленной сети (где связи имеют направление) мы обычно определяем две отдельные меры степени центральности, а именно степень и превосходить. Соответственно, степень - это количество связей, направленных на узел, а исходящая степень - это количество связей, которые узел направляет другим. Когда узы связаны с некоторыми положительными аспектами, такими как дружба или сотрудничество, несоответствие часто интерпретируется как форма популярности, а выходящая из него - как общительность.
Степень центральности вершины , для данного графа с вершины и ребра, определяется как
Для вычисления степени центральности для всех узлов в графе требуется в плотный матрица смежности представление графа, а для ребер принимает в разреженная матрица представление.
Определение центральности на уровне узлов можно распространить на весь граф, и в этом случае мы говорим о централизация графа.[17] Позволять быть узлом с наивысшей степенью центральности в . Позволять быть -узловой связный граф, который максимизирует следующую величину (с являясь узлом с наивысшей степенью центральности в ):
Соответственно степень централизации графа как следует:
Значение максимизируется, когда график содержит один центральный узел, к которому подключены все остальные узлы ( звездный график), и в этом случае
Итак, для любого графика
Центральность близости
В связаны график, то нормализованный центральность близости (или же близость) узла - это средняя длина кратчайший путь между узлом и всеми другими узлами в графе. Таким образом, чем центральнее узел, тем ближе он ко всем остальным узлам.
Близость определялась Алекс Бавелас (1950) как взаимный из дальность,[18][19] то есть:
куда это расстояние между вершинами и . Однако, говоря о центральности по близости, люди обычно ссылаются на ее нормализованную форму, обычно задаваемую предыдущей формулой, умноженной на , куда количество узлов в графе. Эта настройка позволяет сравнивать узлы графов разного размера.
Принимая расстояния из или же к все остальные узлы не имеют отношения к неориентированным графам, тогда как они могут давать совершенно разные результаты в ориентированные графы (например, веб-сайт может иметь высокую степень близости по исходящей ссылке, но низкую центральность по входящим ссылкам).
Гармоническая центральность
В (не обязательно связном) графе гармоническая центральность меняет местами операции суммы и взаимности в определении центральности близости:
куда если нет пути от к . Гармоническая центральность может быть нормализована путем деления на , куда количество узлов в графе.
Гармоническая центральность была предложена Марчиори и Латора (2000)[20] а затем независимо Деккер (2005), используя название «оцененная центральность»,[21] и Роша (2009).[22]
Центральность посредничества
Близость является мерой центральности вершина в пределах график (существует также край промежуточность, которая здесь не обсуждается). Центральность по промежуточности определяет количество раз, когда узел действует как мост на кратчайшем пути между двумя другими узлами. Он был введен как мера для количественной оценки контроля человека над общением между другими людьми в социальной сети. Линтон Фриман.[23] По его замыслу, вершины, которые с высокой вероятностью встречаются на случайно выбранных кратчайший путь между двумя случайно выбранными вершинами имеют высокую промежуточность.
Промежуточность вершины в графике с вершины вычисляются следующим образом:
- Для каждой пары вершин (s,т), вычислить кратчайшие пути между ними.
- Для каждой пары вершин (s,т), определите долю кратчайших путей, проходящих через рассматриваемую вершину (здесь вершина v).
- Просуммируйте эту дробь по всем парам вершин (s,т).
Более компактно промежуточность можно представить как:[24]
куда это общее количество кратчайших путей от узла узел и это количество путей, которые проходят через . Промежуток может быть нормализован путем деления на количество пар вершин, не включая v, который для ориентированные графы является а для неориентированных графов - . Например, в неориентированном звездный график, центральная вершина (которая содержится во всех возможных кратчайших путях) будет иметь промежуточное расстояние (1, если нормализовано), в то время как листья (которые не входят в кратчайшие пути) будут иметь промежуточное значение 0.
С точки зрения вычислений центральность как промежуточности, так и близости всех вершин графа включает вычисление кратчайших путей между всеми парами вершин на графе, что требует время с Алгоритм Флойда-Уоршолла. Однако на разреженных графах Алгоритм Джонсона может быть более эффективным, принимая время. В случае невзвешенных графиков расчеты могут быть выполнены с помощью алгоритма Брандеса.[24] который берет время. Обычно эти алгоритмы предполагают, что графы неориентированы и связаны с учетом петель и кратных ребер. Когда мы конкретно имеем дело с сетевыми графами, часто графы не имеют петель или нескольких ребер для поддержания простых отношений (где ребра представляют собой связи между двумя людьми или вершинами). В этом случае использование алгоритма Брандеса разделит итоговые оценки центральности на 2, чтобы учесть, что каждый кратчайший путь учитывается дважды.[24]
Центральность собственного вектора
Центральность собственного вектора (также называемый собственная центрированность) - мера влияния узел в сеть. Он присваивает относительные оценки всем узлам в сети на основе концепции, согласно которой соединения с узлами с высокими оценками вносят больший вклад в оценку рассматриваемого узла, чем равные соединения с узлами с низкими показателями.[25][4] Googleс PageRank и Кац центральность - варианты центральности собственного вектора.[26]
Использование матрицы смежности для определения центральности собственного вектора
Для данного графа с количество вершин пусть быть матрица смежности, т.е. если вершина связан с вершиной , и иначе. Оценка относительной центральности вершины можно определить как:
куда это набор соседей и является константой. С небольшой переделкой это можно переписать в векторной записи как собственный вектор уравнение
В общем, будет много разных собственные значения для которого существует решение с ненулевым собственным вектором. Поскольку элементы в матрице смежности неотрицательны, существует единственное наибольшее собственное значение, действительное и положительное, по Теорема Перрона – Фробениуса. Это наибольшее собственное значение приводит к желаемой мере центральности.[27] В компонент соответствующего собственного вектора затем дает оценку относительной центральности вершины в сети. Собственный вектор определяется только с точностью до общего множителя, поэтому корректно определены только отношения центральностей вершин. Чтобы определить абсолютную оценку, необходимо нормализовать собственный вектор, например, так, чтобы сумма по всем вершинам была 1 или общее количество вершин п. Итерация мощности один из многих алгоритмы собственных значений который может быть использован для нахождения этого доминирующего собственного вектора.[26] Кроме того, это можно обобщить так, чтобы записи в А могут быть действительными числами, представляющими силу соединения, как в стохастическая матрица.
Кац центральность
Кац центральность[28] является обобщением степени центральности. Центральность по степени измеряет количество прямых соседей, а центральность по Кацу измеряет количество всех узлов, которые могут быть соединены путем, в то время как вклад удаленных узлов наказывается. Математически это определяется как
куда коэффициент затухания в .
Центральность Каца можно рассматривать как вариант центральности собственного вектора. Другая форма центральности Каца - это
По сравнению с выражением центральности собственного вектора, заменяется на
Показано, что[29] главный собственный вектор (связанный с наибольшим собственным значением , матрица смежности) является пределом центральности Каца при подходы снизу.
Центральное место в рейтинге страниц
PageRank удовлетворяет следующему уравнению
куда
это количество соседей узла (или количество исходящих ссылок в ориентированном графе). По сравнению с центральностью собственного вектора и центральностью по Кацу, одним из основных отличий является коэффициент масштабирования . Еще одно различие между PageRank и центральностью собственного вектора заключается в том, что вектор PageRank является левым собственным вектором (обратите внимание на коэффициент имеет обратные индексы).[30]
Центральность перколяции
Существует множество критериев центральности для определения «важности» отдельного узла в сложной сети. Однако эти меры количественно определяют важность узла с чисто топологической точки зрения, и значение узла никоим образом не зависит от «состояния» узла. Он остается постоянным независимо от динамики сети. Это верно даже для взвешенных мер промежуточности. Однако узел вполне может быть расположен в центре с точки зрения центральности промежуточности или другой меры центральности, но не может быть «центрально» расположен в контексте сети, в которой есть просачивание. Распространение «заражения» происходит в сложных сетях по ряду сценариев. Например, вирусная или бактериальная инфекция может распространяться через социальные сети людей, известные как контактные сети. Распространение болезни также можно рассматривать на более высоком уровне абстракции, рассматривая сеть городов или населенных пунктов, связанных автомобильным, железнодорожным или воздушным сообщением. Компьютерные вирусы могут распространяться по компьютерным сетям. Слухи или новости о деловых предложениях и сделках также могут распространяться через социальные сети людей. Во всех этих сценариях «инфекция» распространяется по звеньям сложной сети, изменяя «состояния» узлов по мере своего распространения, с возможностью восстановления или иным образом. Например, в эпидемиологическом сценарии люди переходят из «восприимчивого» в «инфицированное» состояние по мере распространения инфекции. Состояния, которые отдельные узлы могут принимать в приведенных выше примерах, могут быть двоичными (например, получена / не получена новость), дискретными (восприимчивые / инфицированные / восстановленные) или даже непрерывными (например, доля инфицированных людей в городе ) по мере распространения заразы. Общей чертой всех этих сценариев является то, что распространение заражения приводит к изменению состояний узлов в сетях. Имея это в виду, была предложена центральность перколяции (PC), которая конкретно измеряет важность узлов с точки зрения помощи перколяции по сети. Эта мера была предложена Piraveenan et al.[31]
Центральность перколяции определяется для данного узла в данный момент времени как доля «просачиваемых путей», которые проходят через этот узел. «Перколированный путь» - это кратчайший путь между парой узлов, где исходный узел пронизан (например, заражен). Целевой узел может быть перколированным, неперколированным или частично перколированным.
куда это общее количество кратчайших путей от узла узел и это количество путей, которые проходят через . Состояние перколяции узла вовремя обозначается и два особых случая: когда что указывает на неперколированное состояние во время тогда как когда что указывает на полностью перколированное состояние во время . Значения между ними указывают на частично пропитанные состояния (например, в сети поселков это будет процент инфицированных в этом городе).
Прилагаемые веса к путям перколяции зависят от уровней перколяции, назначенных исходным узлам, исходя из предположения, что чем выше уровень перколяции исходного узла, тем более важны пути, исходящие от этого узла. Узлы, которые лежат на кратчайших путях, исходящих из узлов с высокой степенью перколяции, поэтому потенциально более важны для перколяции. Определение ПК также можно расширить, включив в него веса целевых узлов. Расчет центральности перколяции выполняется в время с эффективной реализацией, принятой из быстрого алгоритма Брандеса, и если в расчетах необходимо учитывать веса целевых узлов, время наихудшего случая равно .
Межкликовая центральность
Межкликовая центральность одного узла в сложном графе определяет возможность подключения узла к разным клики. Узел с высокой степенью перекрестной связности облегчает распространение информации или болезни в графе. Клики - это подграфы, в которых каждый узел связан с каждым другим узлом в клике. Кросс-кликовая связность узла для данного графа с вершины и ребра, определяется как куда - количество клик, в которые вершина принадлежит. Эта мера использовалась в [32] но впервые был предложен Эвереттом и Боргатти в 1998 году, где они назвали это центральностью с перекрытием клики.
Централизация Фримена
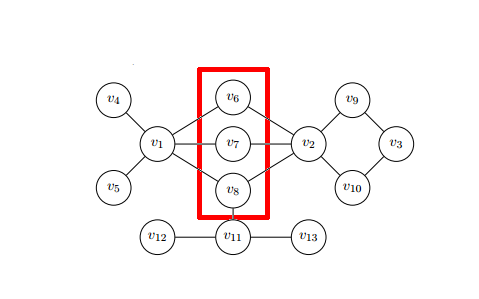
В централизация любой сети является мерой того, насколько центральным является ее самый центральный узел по отношению к тому, насколько центральными являются все остальные узлы.[11] Затем меры централизации (а) вычисляют сумму различий в центральности между самым центральным узлом в сети и всеми другими узлами; и (б) разделить это количество на теоретически наибольшую сумму разностей в любой сети того же размера.[11] Таким образом, каждая мера центральности может иметь свою меру централизации. Определяется формально, если любая мера центральности точки , если является самой крупной такой мерой в сети, и если:
- наибольшая сумма различий в центральности точки для любого графа с таким же количеством узлов централизация сети:[11]
Меры центральности, основанные на различиях
Чтобы получить лучшие результаты при ранжировании узлов данной сети, в [33] используются меры несходства (специфичные для теории классификации и интеллектуального анализа данных) для обогащения мер центральности в сложных сетях. Это проиллюстрировано центральность собственного вектора, вычисляя центральность каждого узла посредством решения задачи на собственные значения
куда (координатно-координационный продукт) и произвольный несходство матрица, определяемая посредством несимметричных мер, например, Жаккар несходство, данное
Если эта мера позволяет нам количественно оценить топологический вклад (поэтому он называется центральностью вклада) каждого узла в центральность данного узла, имея больший вес / релевантность, эти узлы с большим несходством, поскольку они позволяют данному узлу доступ к узлы, которые сами не могут получить доступ напрямую.
Примечательно, что неотрицательно, потому что и неотрицательные матрицы, поэтому мы можем использовать Теорема Перрона – Фробениуса чтобы гарантировать, что указанная выше проблема имеет уникальное решение для λ = λМаксимум с c неотрицательный, что позволяет нам сделать вывод о центральном положении каждого узла в сети. Следовательно, центральность i-го узла равна
куда - количество узлов в сети. Несколько мер и сетей несходства были протестированы в [34] получение улучшенных результатов в изученных случаях.
Расширения
Эмпирические и теоретические исследования расширили понятие центральности в контексте статических сетей до динамической центральности.[35] в контексте зависящих от времени и темпоральных сетей.[36][37][38]
Для обобщения взвешенных сетей см. Opsahl et al. (2010).[39]
Концепция центральности была распространена и на групповой уровень. Например, группа посредственности центральность показывает долю геодезических, соединяющих пары не входящих в группу членов, которые проходят через группу.[40][41]
Смотрите также
Примечания и ссылки
- ^ Ньюман, M.E.J. 2010 г. Сети: Введение. Оксфорд, Великобритания: Издательство Оксфордского университета.
- ^ а б c d Bonacich, Филипп (1987). «Власть и центральность: семейство мер». Американский журнал социологии. 92 (5): 1170–1182. Дои:10.1086/228631.
- ^ а б c d е ж Боргатти, Стивен П. (2005). «Центральность и сетевой поток». Социальные сети. 27: 55–71. CiteSeerX 10.1.1.387.419. Дои:10.1016 / j.socnet.2004.11.008.
- ^ а б Кристиан Ф. А. Негре, Уриэль Н. Морзан, Хайди П. Хендриксон, Ританкар Пал, Джордж П. Лиси, Дж. Патрик Лориа, Иван Ривальта, Джунмин Хо, Виктор С. Батиста. (2018). «Центральность собственного вектора для характеристики аллостерических путей белков». Труды Национальной академии наук. 115 (52): E12201 – E12208. Дои:10.1073 / pnas.1810452115. ЧВК 6310864. PMID 30530700.CS1 maint: несколько имен: список авторов (связь)
- ^ а б c d Боргатти, Стивен П .; Эверетт, Мартин Г. (2006). "Теоретико-графическая перспектива центральности". Социальные сети. 28 (4): 466–484. Дои:10.1016 / j.socnet.2005.11.005.
- ^ а б Бензи, Микеле; Климко, Кристина (2013). «Матричный анализ различных мер центральности». Журнал SIAM по матричному анализу и приложениям. 36 (2): 686–706. arXiv:1312.6722. Дои:10.1137/130950550. S2CID 7088515.
- ^ Михалак, Адития, Щепаньски, Равиндран и Дженнингс arXiv:1402.0567
- ^ Ху, Синвэй; Шепли, Ллойд (2003). «О распределении полномочий в организациях». Игры и экономическое поведение. 45: 132–170. Дои:10.1016 / s0899-8256 (03) 00130-1.
- ^ Ху, Синвэй (2020). «Сортировка больших данных по выявленным предпочтениям применительно к рейтингу колледжей». Журнал больших данных. 7. Дои:10.1186 / s40537-020-00300-1.
- ^ Кракхардт, Дэвид (Июнь 1990 г.). «Оценка политического ландшафта: структура, познание и власть в организациях». Административная наука ежеквартально. 35 (2): 342–369. Дои:10.2307/2393394. JSTOR 2393394.
- ^ а б c d Фриман, Линтон С. (1979), «центральность в социальных сетях: концептуальное уточнение» (PDF), Социальные сети, 1 (3): 215–239, CiteSeerX 10.1.1.227.9549, Дои:10.1016/0378-8733(78)90021-7, заархивировано из оригинал (PDF) на 2016-02-22, получено 2014-07-31
- ^ а б Юрист, Гленн (2015). «Понимание распространяемой мощности всех узлов в сети: непрерывная перспектива». Научный представитель. 5: 8665. arXiv:1405.6707. Bibcode:2015НатСР ... 5Э8665Л. Дои:10.1038 / srep08665. ЧВК 4345333. PMID 25727453.
- ^ да Силва, Ренато; Виана, Матеус; да Ф. Коста, Лучано (2012). «Прогнозирование вспышки эпидемии по индивидуальным особенностям распространителей». J. Stat. Механизм .: Theory Exp. 2012 (7): P07005. arXiv:1202.0024. Bibcode:2012JSMTE..07..005A. Дои:10.1088 / 1742-5468 / 2012/07 / p07005. S2CID 2530998.
- ^ Бауэр, Франк; Лизье, Джозеф (2012). «Выявление влиятельных распространителей и эффективная оценка числа инфекций в моделях эпидемии: метод подсчета ходьбы». Europhys Lett. 99 (6): 68007. arXiv:1203.0502. Bibcode:2012EL ..... 9968007B. Дои:10.1209/0295-5075/99/68007. S2CID 9728486.
- ^ Сикич, Миля; Ланчич, Ален; Антулов-Фантулин, Нино; Стефанич, Хрвое (2013). «Эпидемическая центральность - существует ли недооценка эпидемического воздействия периферийных узлов сети?». Европейский физический журнал B. 86 (10): 1–13. arXiv:1110.2558. Bibcode:2013EPJB ... 86..440S. Дои:10.1140 / epjb / e2013-31025-5. S2CID 12052238.
- ^ Ghoshal, G .; Барабси, А. Л. (2011). «Рейтинг стабильности и сверхстабильных узлов в сложных сетях». Nat Commun. 2: 394. Bibcode:2011НатКо ... 2..394G. Дои:10.1038 / ncomms1396. PMID 21772265.
- ^ Фриман, Линтон С. «Центральное место в концептуальном разъяснении социальных сетей». Социальные сети 1.3 (1979): 215–239.
- ^ Алекс Бавелас. Паттерны общения в целевых группах. J. Acoust. Soc. Являюсь, 22(6):725–730, 1950.
- ^ Сабидусси, G (1966). «Индекс центральности графа». Психометрика. 31 (4): 581–603. Дои:10.1007 / bf02289527. HDL:10338.dmlcz / 101401. PMID 5232444. S2CID 119981743.
- ^ Марчиори, Массимо; Латора, Вито (2000), «Гармония в маленьком мире», Physica A: Статистическая механика и ее приложения, 285 (3–4): 539–546, arXiv:cond-mat / 0008357, Bibcode:2000PhyA..285..539M, Дои:10.1016 / s0378-4371 (00) 00311-3, S2CID 10523345
- ^ Деккер, Энтони (2005). «Концептуальная дистанция в анализе социальных сетей». Журнал социальной структуры. 6 (3).
- ^ Янник Рошат. Центральность по близости распространяется на несвязные графы: индекс гармонической центральности (PDF). Приложения анализа социальных сетей, ASNA 2009.
- ^ Фриман, Линтон (1977). «Набор мер центральности, основанный на промежуточности». Социометрия. 40 (1): 35–41. Дои:10.2307/3033543. JSTOR 3033543.
- ^ а б c Брандес, Ульрик (2001). «Более быстрый алгоритм определения центральности посредственности» (PDF). Журнал математической социологии. 25 (2): 163–177. CiteSeerX 10.1.1.11.2024. Дои:10.1080 / 0022250x.2001.9990249. S2CID 13971996. Получено 11 октября, 2011.
- ^ М. Э. Дж. Ньюман. «Математика сетей» (PDF). Получено 2006-11-09. Цитировать журнал требует
| журнал =(помощь) - ^ а б «Американское математическое общество».
- ^ М. Э. Дж. Ньюман. «Математика сетей» (PDF). Получено 2006-11-09. Цитировать журнал требует
| журнал =(помощь) - ^ Кац, Л. 1953. Новый индекс статуса, полученный на основе социометрического индекса. Психометрика, 39–43.
- ^ Bonacich, P (1991). «Одновременные групповые и индивидуальные центральности». Социальные сети. 13 (2): 155–168. Дои:10.1016 / 0378-8733 (91) 90018-о.
- ^ Как Google оценивает веб-страницы? В архиве 31 января 2012 г. Wayback Machine 20Q: о сетевой жизни
- ^ Пиравеенан, М .; Прокопенко, М .; Хоссейн, Л. (2013). "Центральность перколяции: количественная оценка теоретико-графического влияния узлов во время перколяции в сетях". PLOS ONE. 8 (1): e53095. Bibcode:2013PLoSO ... 853095P. Дои:10.1371 / journal.pone.0053095. ЧВК 3551907. PMID 23349699.
- ^ Фагани, Мохамамд Реза (2013). «Исследование механизмов распространения и обнаружения XSS-червей в социальных сетях». IEEE Transactions по информационной криминалистике и безопасности. 8 (11): 1815–1826. Дои:10.1109 / TIFS.2013.2280884. S2CID 13587900.
- ^ Альварес-Сокорро, А. Дж .; Herrera-Almarza, G.C .; Гонсалес-Диас, Л. А. (25 ноября 2015 г.). «Собственная центрированность, основанная на показателях несходства, выявляет центральные узлы в сложных сетях». Научные отчеты. 5: 17095. Bibcode:2015НатСР ... 517095А. Дои:10.1038 / srep17095. ЧВК 4658528. PMID 26603652.
- ^ Альварес-Сокорро, А.Дж .; Эррера-Альмарса; Гонсалес-Диас, Л.А. «Дополнительная информация о собственной центрированности, основанная на показателях несходства, выявляет центральные узлы в сложных сетях» (PDF). Издательская группа "Природа".
- ^ Braha, D .; Бар-Ям Ю. (2006). «От центральности к временной славе: динамическое центральное положение в сложных сетях». Сложность. 12 (2): 59–63. arXiv:физика / 0611295. Bibcode:2006Cmplx..12b..59B. Дои:10.1002 / cplx.20156. S2CID 1776280.
- ^ Hill, S.A .; Браха, Д. (2010). «Динамическая модель зависящих от времени сложных сетей». Физический обзор E. 82 (4): 046105. arXiv:0901.4407. Bibcode:2010PhRvE..82d6105H. Дои:10.1103 / Physreve.82.046105. PMID 21230343. S2CID 3219870.
- ^ Гросс Т. и Саяма Х. (ред.). 2009 г. Адаптивные сети: теория, модели и приложения. Springer.
- ^ Холм П. и Сарамяки Дж. 2013. Темпоральные сети. Springer.
- ^ Опсаль, Тор; Агниссенс, Филип; Скворец, Джон (2010). «Центральность узла в взвешенных сетях: степень обобщения и кратчайшие пути». Социальные сети. 32 (3): 245–251. Дои:10.1016 / j.socnet.2010.03.006. Архивировано из оригинал на 2018-02-26. Получено 2010-04-23.
- ^ Эверетт, М. Г. и Боргатти, С. П. (2005). Повышение центральности. В П. Дж. Кэррингтоне, Дж. Скотте и С. Вассермане (редакторы), Модели и методы анализа социальных сетей (стр. 57–76). Нью-Йорк: Издательство Кембриджского университета.
- ^ Пузис, Р., Ягил, Д., Еловичи, Ю., Браха, Д. (2009).Совместная атака на анонимность пользователей Интернета В архиве 2013-12-07 в Wayback Machine, Интернет-исследования 19(1)
дальнейшее чтение
- Koschützki, D .; Lehmann, K. A .; Peeters, L .; Richter, S .; Тенфельде-Подель, Д., Злотовски, О. (2005) Индексы центральности. В Брандес, У. и Эрлебах, Т. (ред.) Сетевой анализ: методологические основы, стр. 16–61, LNCS 3418, Springer-Verlag.






















![H = sum _ {{j = 1}} ^ {{| Y |}} [C_ {D} (y *) - C_ {D} (y_ {j})]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9666585dcf8a4913865d385f3e974c6891c879f3)
![{ Displaystyle C_ {D} (G) = { frac { sum _ {i = 1} ^ {| V |} [C_ {D} (v *) - C_ {D} (v_ {i})] }{ЧАС}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29d1d78ee22a5ca4dbfab56ee81d15d2206300f0)



![{ Displaystyle C_ {D} (G) = { frac { sum _ {i = 1} ^ {| V |} [C_ {D} (v *) - C_ {D} (v_ {i})] } {| V | ^ {2} -3 | V | +2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7551bf124c85cb266574ec4aab363a0f9d6eb05c)









































![PC ^ t (v) = frac {1} {N-2} sum_ {s neq v neq r} frac { sigma_ {sr} (v)} { sigma_ {sr}} frac { {x ^ t} _s} {{ sum {[{x ^ t} _i}]} - {x ^ t} _v}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff9329766cc6f7d93f19d9703dd81488fb14b5e7)






















