WikiDer > График покрытия

Covering graph

в математический дисциплина теория графов, а график C это покрывающий граф другого графа грамм если есть карта покрытия из множества вершин C к множеству вершин грамм. Покрывающая карта ж это сюрприз и локальный изоморфизм: район вершины v в C нанесен на карту биективно на окрестности ж(v) в грамм.

Период, термин поднимать часто используется как синоним покрывающего графа связного графа.

Хотя это может вводить в заблуждение, нет (очевидной) связи между покрывающим графом и крышка вершины или же край крышки.

Комбинаторная формулировка покрывающих графов немедленно обобщается на случай мультиграфы. Если мы отождествляем мультиграф с одномерным клеточным комплексом, покрывающий граф будет не чем иным, как частным примером перекрытия из топологические пространства, так что терминология теории накрытий доступна; говорят накрывающая группа преобразований, универсальное накрытие, абелево накрытие и максимальное абелево покрытие.[1]

Определение

Позволять грамм = (V1, E1) и C = (V2, E2) - два графа, и пусть ж: V2 → V1 быть сюрприз. потом ж это карта покрытия из C к грамм если для каждого v ∈ V2, ограничение ж к район из v биекция на окрестность ж(v) в грамм. Иначе говоря, ж сопоставляет ребра, инцидентные v взаимно однозначно на ребра, инцидентные ж(v).

Если существует карта покрытия из C к грамм, тогда C это покрывающий граф, или поднимать, из грамм. An h-лифт есть лифт такой, что накрывающее отображение ж обладает тем свойством, что для каждой вершины v из грамм, это волокно ж−1(v) точно час элементы.

Примеры

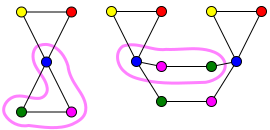
На следующем рисунке график C покрывающий граф графа ЧАС.

Покрытие-граф-4.svg

Покрывающая карта ж из C к ЧАС обозначается цветами. Например, обе синие вершины C отображаются в синюю вершину ЧАС. Карта ж сюръекция: каждая вершина ЧАС имеет прообраз в C. Более того, ж биективно отображает каждую окрестность вершины v в C на окрестность вершины ж(v) в ЧАС.

Например, пусть v быть одной из фиолетовых вершин в C; у него есть два соседа в C, зеленая вершина ты и синяя вершина т. Аналогично пусть v′ - фиолетовая вершина в ЧАС; у него есть два соседа в ЧАС, зеленая вершина ты′ И синяя вершина т′. Отображение ж ограниченный {т, ты, v} является биекцией на {т′, ты′, v′}. Это показано на следующем рисунке:

Покрытие-граф-4-a.svg

Аналогичным образом можно проверить, что окрестность синей вершины в C взаимно однозначно отображается на окрестность синей вершины в ЧАС:

Покрытие-граф-4-b.svg

Двойная крышка

В приведенном выше примере каждая вершина ЧАС имеет ровно 2 прообраза в C. Следовательно ЧАС это 2-кратная крышка или двойная крышка из C.

Для любого графика грамм, можно построить двусторонняя двойная обложка из грамм, который является двудольный граф и двойная обложка грамм. Двудольное двойное покрытие грамм это тензорное произведение графов грамм × K2:

Покрытие-граф-2.svg

Если грамм уже двудольный, его двудольное двойное покрытие состоит из двух непересекающихся копий грамм. Граф может иметь много разных двойных покрытий, кроме двудольного двойного покрытия.

Универсальный чехол

Для любого связного графа грамм, можно построить его универсальный накрывающий граф.[2] Это пример более общего универсальный чехол понятие из топологии; топологическое требование, чтобы универсальное покрытие было односвязный переводится в терминах теории графов как требование, чтобы он был ацикличным и связным; это дерево. Универсальный накрывающий граф единственен (с точностью до изоморфизма). Если грамм это дерево, тогда грамм сам является универсальным накрывающим графом грамм. Для любого другого конечного связного графа грамм, универсальный накрывающий граф грамм - счетно бесконечное (но локально конечное) дерево.

Универсальный накрывающий граф Т связного графа грамм можно построить следующим образом. Выбираем произвольную вершину р из грамм в качестве отправной точки. Каждая вершина Т прогулка без возврата, которая начинается с р, то есть последовательность ш = (р, v1, v2, ..., vп) вершин грамм такой, что

  • vя и vя+1 соседствуют в грамм для всех я, т.е. ш это прогулка
  • vя-1 ≠ vя+1 для всех я, т.е. w не имеет возврата.

Тогда две вершины Т смежны, если одно является простым продолжением другого: вершина (р, v1, v2, ..., vп) смежна с вершиной (р, v1, v2, ..., vп-1). С точностью до изоморфизма одно и то же дерево Т строится независимо от выбора отправной точки р.

Покрывающая карта ж отображает вершину (р) в Т к вершине р в грамм, а вершина (р, v1, v2, ..., vп) в Т к вершине vп в грамм.

Примеры универсальных чехлов

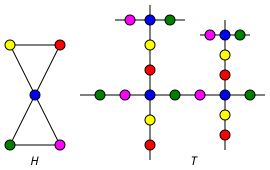
На следующем рисунке показан универсальный покрывающий граф. Т графа ЧАС; цвета указывают на карту покрытия.

Покрытие-граф-5.svg

Для любого k, все k-регулярные графики имеют ту же универсальную обложку: бесконечное k-регулярное дерево.

Топологический кристалл

Бесконечнократный абелев покрывающий граф конечного (мульти) графа называется топологическим кристаллом, абстракцией кристаллических структур. Например, кристалл алмаза как граф является графом максимального абелевого покрытия четырехреберного дипольный график. Эта точка зрения в сочетании с идеей «стандартных реализаций» оказывается полезной при систематическом проектировании (гипотетических) кристаллов.[1]

Плоское покрытие

Основная статья: Плоское покрытие

А плоское покрытие графа - это конечный граф покрытия, который сам является планарный граф. Свойство иметь плоское покрытие можно охарактеризовать: запрещенные несовершеннолетние, но точная характеристика этой формы остается неизвестной. Каждый граф с встраивание в проективная плоскость имеет плоское покрытие, идущее от ориентируемая двойная крышка проективной плоскости; В 1988 году Сейя Нагами предположил, что это единственные графы с плоскими покрытиями, но это осталось недоказанным.[3]

Графики напряжения

Обычный способ формирования покрывающих графов использует графики напряжения, в котором дротики данного графа грамм (то есть пары ориентированных ребер, соответствующие неориентированным ребрам грамм) помечены обратными парами элементов из некоторого группа. Производный граф графа напряжений имеет вершинами пары (v,Икс) куда v является вершиной грамм и Икс является элементом группы; дротик из v к ш помечены элементом группы у в грамм соответствует ребру из (v,Икс) к (ш,ху) в производном графе.

Таким образом, универсальное покрытие можно рассматривать как производный график графика напряжения, в котором ребра остовное дерево графа помечены единичным элементом группы, а каждая оставшаяся пара дротиков помечена отдельным порождающим элементом свободная группа. Таким образом, двудольный дубль можно рассматривать как производный график графика напряжения, в котором каждый дротик помечен ненулевым элементом группы второго порядка.

Примечания

  1. ^ а б Сунада, Тошиказу (2012). Топологическая кристаллография - с точки зрения дискретного геометрического анализа -. Springer.
  2. ^ Англюин 1980.
  3. ^ Глинены, Петр (2010), "20 лет гипотезе Негами о плоском покрытии" (PDF), Графы и комбинаторика, 26 (4): 525–536, CiteSeerX 10.1.1.605.4932, Дои:10.1007 / s00373-010-0934-9, МИСТЕР 2669457.

Рекомендации