WikiDer > Циклогон

Cyclogon

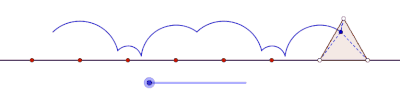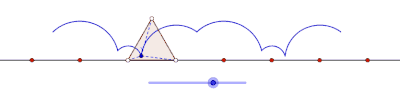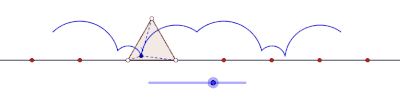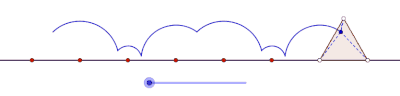
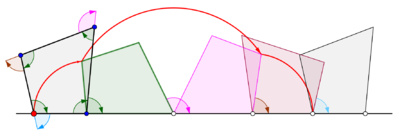
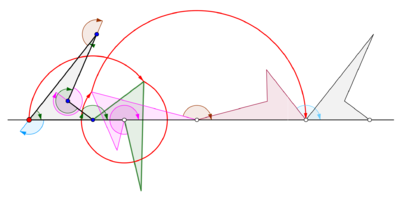
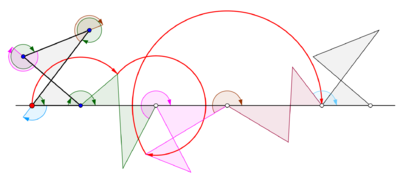
В математика, в геометрия, а циклогон кривая, идущая по вершине многоугольник катится, не поскользнувшись прямая линия.[1][2] Нет никаких ограничений по характеру многоугольника. Это может быть правильный многоугольник, например равносторонний треугольник или квадрат. Многоугольник даже не обязательно должен быть выпуклым: это может быть даже многоугольник в форме звезды. В более общем плане также рассматривались кривые, очерченные не вершинами, а точками. В таких случаях предполагается, что точка отслеживания жестко прикреплена к многоугольнику. Если точка трассировки расположена за пределами многоугольника, кривая называется кривой. вытянутый циклогон, а если он лежит внутри многоугольника, он называется свернуть циклогон.

В пределе, когда число сторон увеличивается до бесконечности, циклогон становится циклоида.[3]

У циклогона есть интересное свойство относительно его площади. [3] Позволять А обозначим площадь области над линией и под одной из дуг, пусть п обозначим площадь катящегося многоугольника, и пусть C обозначают площадь диска, ограничивающего многоугольник. Для каждого циклогона, порожденного правильным многоугольником,

Примеры

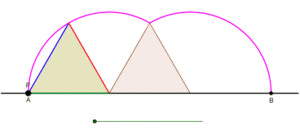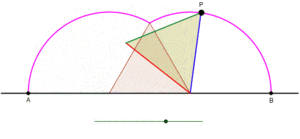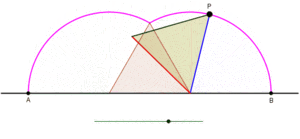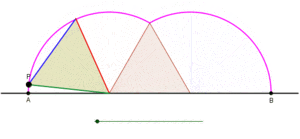
Циклогоны, порожденные равносторонним треугольником и квадратом

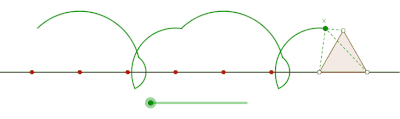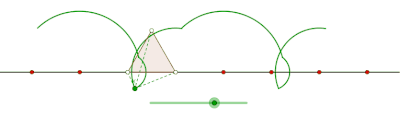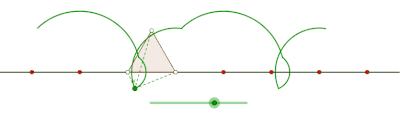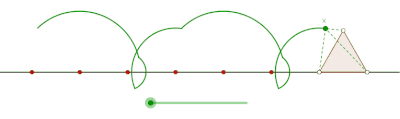
Анимация, показывающая создание одной дуги циклогона равносторонним треугольником, когда треугольник катится по прямой без скольжения.
Анимация, показывающая создание одной дуги циклогона квадратом, когда квадрат катится по прямой без проскальзывания.

 

Вытяжной циклогон, образованный равносторонним треугольником

Анимация, показывающая прорисовку вытянутого циклогона в виде равностороннего треугольника, который катится по прямой без пропусков. Точка отслеживания X находится за пределами круга треугольника.

 

Curtate циклогон, образованный равносторонним треугольником

Анимация, показывающая обводку свернувшегося циклогона в виде равностороннего треугольника, который катится по прямой без пропусков. Точка отслеживания Y находится внутри круга треугольника.

Циклогоны, порожденные четырехугольниками

Циклогон, порожденный выпуклым четырехугольником
Циклогон, порожденный невыпуклым четырехугольником
Циклогон, порожденный звездообразным четырехугольником

Обобщенные циклогоны

Циклогон получается, когда многоугольник катится по прямой. Предположим, что правильный многоугольник перекатывается через край другого многоугольника. Предположим также, что точка отслеживания - это не точка на границе многоугольника, а, возможно, точка внутри многоугольника или вне многоугольника, но лежащая в плоскости многоугольника. В этой более общей ситуации, пусть кривая проводится точкой z на правильном многоугольном диске с n сторонами, катящимся вокруг другого правильного многоугольного диска с m сторонами. Предполагается, что ребра двух правильных многоугольников имеют одинаковую длину. Точка z, жестко прикрепленная к n-угольнику, очерчивает дугу, состоящую из n дуг окружности, прежде чем периодически повторять узор. Эта кривая называется трохогон - ан эпитрохогон если n-угольник катится за пределы m-угольника, а гипотрохогон если он катится внутри м-угольника. Трохогон изогнут, если z находится внутри n-угольника, и вытянут (с петлями), если z находится вне n-угольника. Если z находится в вершине, он отслеживает эпициклогон или гипоциклогон.[4]

Смотрите также

Рекомендации

  1. ^ Том М. Апостол, Мамикон Мнацаканян (2012). Новые горизонты в геометрии. Математическая ассоциация Америки. п.68. ISBN 9780883853542.
  2. ^ Кен Кэвинесс. «Циклогоны». Вольфрам Демонстрационный проект. Получено 23 декабря 2015.
  3. ^ а б Апостол Т.М., Мнацаканян М.А. (1999). «Циклоидные области без зубного камня» (PDF). Математические горизонты. 7 (1): 12–16. Архивировано из оригинал (PDF) на 2005-01-30. Получено 23 декабря 2015.
  4. ^ Том М. Апостопл и Мамикон А. Мнацакнян (сентябрь 2002 г.). «Обобщенные циклогоны» (PDF). Математические горизонты. Архивировано из оригинал (PDF) на 2005-01-30. Получено 23 декабря 2015.