WikiDer > Экваториальная система координат

В экваториальная система координат это система небесных координат широко используется для указания позиций небесные объекты. Это может быть реализовано в сферический или же прямоугольный координаты, оба определены источник в центре земной шар, а фундаментальная плоскость состоящий из проекция земных экватор на небесная сфера (формируя небесный экватор), основное направление к весеннему равноденствие, а правша соглашение.[1][2]
Начало координат в центре Земли означает, что координаты геоцентрический, то есть если смотреть из центра Земли, как если бы прозрачный.[3] Фундаментальная плоскость и основное направление означают, что система координат, выровненная с земной экватор и столб, не вращается вместе с Землей, но остается относительно неподвижным на фоне звезды. Правостороннее соглашение означает, что координаты увеличиваются к северу от основной плоскости и к востоку от нее.
Основное направление
Это описание ориентация системы отсчета несколько упрощено; ориентация не совсем фиксированная. Медленное движение оси Земли, прецессия, вызывает медленный, непрерывный поворот системы координат на запад вокруг полюсов эклиптика, совершая один круг примерно за 26000 лет. На это накладывается меньшее движение эклиптики и небольшое колебание оси Земли, нутация.[4]
Для определения точного первичного направления эти движения требуют указания равноденствие определенной даты, известной как эпоха, при предоставлении позиции. Три наиболее часто используемых:
- Среднее равноденствие стандартной эпохи (обычно J2000.0, но может включать B1950.0, B1900.0 и т. д.)
- - это фиксированное стандартное направление, позволяющее напрямую сравнивать позиции, созданные в разные даты.
- Среднее равноденствие даты
- является пересечением эклиптики «даты» (то есть эклиптики в ее положении на «дату») с точкой иметь в виду экватор (то есть, экватор вращается прецессией до своего положения на «дату», но без небольших периодических колебаний нутации). Обычно используется в планетарных орбита расчет.
- Истинное равноденствие даты
- является пересечением эклиптики "даты" с истинный экватор (то есть средний экватор плюс нутация). Это фактическое пересечение двух плоскостей в любой конкретный момент с учетом всех движений.
Таким образом, обычно указывается положение в экваториальной системе координат. истинное равноденствие и экватор даты, среднее равноденствие и экватор J2000.0, или похожие. Обратите внимание, что здесь нет «средней эклиптики», так как эклиптика не подвержена небольшим периодическим колебаниям.[5]
Сферические координаты
Использование в астрономии
А звездасферические координаты часто выражаются в виде пары, прямое восхождение и склонение, без расстояние координировать. Направление достаточно удаленных объектов одинаково для всех наблюдателей, и это направление удобно задавать с одинаковыми координатами для всех. Напротив, в горизонтальная система координат, положение звезды отличается от наблюдателя к наблюдателю в зависимости от их положения на поверхности Земли и непрерывно меняется с вращением Земли.
Телескопы оснащен экваториальные горы и установка кругов использовать экваториальную систему координат для поиска объектов. Установка кругов в сочетании с карта звездного неба или же эфемериды позволяют легко наводить телескоп на известные объекты на небесной сфере.
Склонение
Символ склонения δ, (нижний регистр «дельта», сокращенно DEC) измеряет угловое расстояние до объекта, перпендикулярное небесному экватору, положительное на север и отрицательное на юг. Например, северный полюс мира имеет склонение + 90 °. Источником склонения является небесный экватор, который представляет собой проекцию экватора Земли на небесную сферу. Склонение аналогично земному широта.[6][7][8]
Прямое восхождение
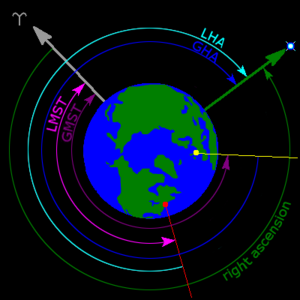
Символ прямого восхождения α, (нижний регистр "альфа", сокращенно RA) измеряет угловое расстояние от объекта на восток вдоль небесный экватор из весеннего равноденствие к часовой круг проходя через объект. Точка весеннего равноденствия - одна из двух, где эклиптика пересекает небесный экватор. По аналогии с земным долгота, прямое восхождение обычно измеряется в сидерический часы, минуты и секунды вместо градусов, результат метода измерения прямого восхождения определение времени прохождения объектов по меридиану как Земля вращается. Есть 360°/24час = 15 ° за один час прямого восхождения и 24час прямого восхождения вокруг всего небесный экватор.[6][9][10]
При совместном использовании прямое восхождение и склонение обычно обозначаются сокращенно RA / Dec.
Часовой угол
Альтернативно прямое восхождение, часовой угол (сокращенно HA или LHA, местный часовой угол), левосторонняя система, измеряет угловое расстояние объекта на запад вдоль небесный экватор от наблюдателя меридиан к часовой круг проходя через объект. В отличие от прямого восхождения, часовой угол всегда увеличивается с увеличением вращение Земли. Часовой угол можно рассматривать как средство измерения времени с момента верхнего кульминация, момент, когда объект касается верхнего меридиана.
Считается, что кульминационная звезда на меридиане наблюдателя имеет нулевой часовой угол (0час). Один звездный час (приблизительно 0,9973 солнечные часы) позже вращение Земли перенесет звезду к западу от меридиана, и ее часовой угол будет равен 1час. При расчете топоцентрический явления, прямое восхождение может быть преобразовано в часовой угол как промежуточный шаг.[11][12][13]
Прямоугольные координаты
Геоцентрические экваториальные координаты

Есть ряд прямоугольный варианты экваториальных координат. У всех есть:
- В источник в центре земной шар.
- Фундаментальный самолет в плоскости экватора Земли.
- Основное направление ( Икс оси) к весеннему равноденствие, то есть место, где солнце пересекает небесный экватор в северном направлении в его кажущемся годовом обороте вокруг эклиптика.
- А правша соглашение, определяя у ось 90 ° на восток в основной плоскости и z ось вдоль северной полярной оси.
Системы отсчета не вращаются вместе с Землей (в отличие от В центре Земли, фиксировано на Земле кадров), оставаясь всегда направленным в сторону равноденствие, и дрейфует со временем с движениями прецессия и нутация.
- В астрономия:[14]
- В положение Солнца часто задается в геоцентрических экваториальных прямоугольных координатах Икс, Y, Z и четвертая координата расстояния, р (= √Икс2 + Y2 + Z2), в единицах астрономическая единица.
- Позиции планеты и другие Солнечная система тела часто задаются в геоцентрических экваториальных прямоугольных координатах ξ, η, ζ и четвертая координата расстояния, δ (равно √ξ2 + η2 + ζ2), в единицах астрономическая единица.Эти прямоугольные координаты связаны с соответствующими сферическими координатами соотношением
- В астродинамика:[15]
- Позиции искусственной Земли спутники указаны в геоцентрический экваториальный координаты, также известные как геоцентрический экваториальный инерциальный (GEI), Инерциальный (ECI), и обычная инерциальная система (КИС), все из которых по определению эквивалентны описанным выше астрономическим геоцентрическим экваториальным прямоугольным системам. В геоцентрической экваториальной системе отсчета Икс, у и z оси часто обозначают я, J и Kсоответственно или кадра основа определяется единичные векторы Я, Ĵ и K̂.
- В Геоцентрическая небесная система отсчета (GCRF) является геоцентрическим эквивалентом Международная небесная система отсчета (ICRF). Его основное направление - равноденствие из J2000.0, и не движется с прецессия и нутация, но в остальном эквивалентен вышеуказанным системам.
| Сферический | Прямоугольный | ||||
|---|---|---|---|---|---|
| Прямое восхождение | Склонение | Расстояние | Общий | Спец. Назначение | |
| Геоцентрический | α | δ | Δ | ξ, η, ζ | Икс, Y, Z (Солнце) |
| Гелиоцентрический | Икс, у, z | ||||
Гелиоцентрические экваториальные координаты
В астрономия, есть также гелиоцентрический прямоугольный вариант экваториальных координат, обозначенный Икс, у, z, у которого есть:
- В источник в центре солнце.
- Фундаментальный самолет в плоскости экватора Земли.
- Основное направление ( Икс оси) к весеннему равноденствие.
- А правша соглашение, определяя у ось 90 ° на восток в основной плоскости и z ось вдоль земной шарСеверная полярная ось.
Этот фрейм во всех смыслах эквивалентен ξ, η, ζ выше, за исключением того, что начало координат удалено в центр солнце. Обычно используется при расчете орбиты планет. Три астрономические прямоугольные системы координат связаны соотношением[17]
Смотрите также
Рекомендации
- ^ Управление морского альманаха, Военно-морская обсерватория США; H.M. Управление морского альманаха; Гринвичская королевская обсерватория (1961). Пояснительное приложение к астрономическим эфемеридам и американским эфемеридам и морскому альманаху. H.M. Канцелярские товары, Лондон (перепечатка 1974 г.). стр.24, 26.
- ^ Валладо, Дэвид А. (2001). Основы астродинамики и приложений. Microcosm Press, Эль-Сегундо, Калифорния. п. 157. ISBN 1-881883-12-4.
- ^ Управление морского альманаха военно-морской обсерватории США; Гидрографическое управление Великобритании; H.M. Офис морского альманаха (2008). Астрономический альманах за 2010 год. Правительство США Типография. п. М2, «видимое место». ISBN 978-0-7077-4082-9.
- ^ Пояснительное приложение (1961), стр.20, 28
- ^ Миус, Жан (1991). Астрономические алгоритмы. Willmann-Bell, Inc., Ричмонд, Вирджиния. п. 137. ISBN 0-943396-35-2.
- ^ а б Питер Даффет-Смит. Практическая астрономия с вашим калькулятором, третье издание. Издательство Кембриджского университета. стр.28–29. ISBN 0-521-35699-7.
- ^ Меир Х. Дегани (1976). Простая астрономия. Doubleday & Company, Inc. стр.216. ISBN 0-385-08854-X.
- ^ Астрономический альманах 2010, п. M4
- ^ Моултон, Лесной Луч (1918). Введение в астрономию. п. 127.
- ^ Астрономический альманах 2010, п. M14
- ^ Питер Даффет-Смит. Практическая астрономия с вашим калькулятором, третье издание. Издательство Кембриджского университета. стр.34–36. ISBN 0-521-35699-7.
- ^ Астрономический альманах 2010, п. M8
- ^ Валладо (2001), стр. 154
- ^ Пояснительное приложение (1961), стр. 24–26
- ^ Валладо (2001), стр. 157, 158
- ^ Пояснительное приложение (1961), сек. 1G
- ^ Пояснительное приложение (1961), стр.20, 27
внешняя ссылка
- ИЗМЕРЕНИЕ НЕБО Краткое руководство по небесной сфере Джеймс Б. Калер, Иллинойский университет
- Небесная экваториальная система координат Университет Небраски-Линкольн
- Исследователи небесных экваториальных координат Университет Небраски-Линкольн

