WikiDer > График Эрреры
| График Эрреры | |
|---|---|
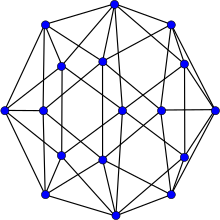 Граф Эрреры | |
| Названный в честь | Альфред Эррера |
| Вершины | 17 |
| Края | 45 |
| Радиус | 3 |
| Диаметр | 4 |
| Обхват | 3 |
| Автоморфизмы | 20 (D10) |
| Хроматическое число | 4 |
| Хроматический индекс | 6 |
| Характеристики | Планарный Гамильтониан |
| Таблица графиков и параметров | |
в математический поле теория графов, то График Эрреры это граф с 17 вершины и 45 края. Альфред Эррера опубликовал его в 1921 году как контрпример к Кемпеошибочное доказательство теорема четырех цветов;[1][2] он был назван в честь Эрреры Хатчинсон и Вагон (1998).[1]
Характеристики
График Эрреры планарный и имеет хроматическое число 4, хроматический индекс 6, радиус 3, диаметр 4 и обхват 3. Все его вершины имеют степень 5 или 6, и это 5-вершинно-связный граф и 5-реберный граф.
Граф Эрреры не является вершинно-транзитивный граф и его полная группа автоморфизмов изоморфна группе группа диэдра порядка 20 группа симметрий десятиугольник, включая как вращения, так и отражения.
В характеристический многочлен графа Эрреры .
Приложение к теореме четырех цветов

В теорема четырех цветов утверждает, что вершины каждого плоского графа можно раскрасить в четыре цвета, так что никакие две соседние вершины не имеют одинаковых цветов. Ошибочное доказательство было опубликовано в 1879 г. Альфред Кемпе, но к 1890 году было обнаружено, что она ошибочна. Теорема о четырех цветах не имела действительного доказательства до 1976 года. Доказательство Кемпе может быть преобразовано в алгоритм раскрашивать планарные графы, что тоже ошибочно. Контрпримеры к его доказательству были найдены в 1890 и 1896 гг. Граф Пуссена), а позже граф Фрича и граф Сойфера предоставили два меньших контрпримера.[3]Однако до работы Эрреры эти контрпримеры не показали, что весь алгоритм раскраски дает сбой. Скорее, они предположили, что все вершины графа, кроме одной, уже были раскрашены, и показали, что метод Кемпе (который якобы изменил раскраску, чтобы распространить ее на все графы) потерпел неудачу в этих предварительно раскрашенных экземплярах. График Эрреры, с другой стороны, представляет собой контрпример ко всему методу Кемпе. Когда этот метод запускается на графе Эрреры, начиная с отсутствия раскрашенных вершин, он может не найти правильную раскраску для всего графа.[1]Кроме того, в отличие от графа Пуссена, все вершины в графе Эррера имеют степень пять или больше. Следовательно, на этом графе невозможно избежать проблемных случаев метода Кемпе, выбирая вершины более низкой степени.
На рисунке показан пример того, как доказательство Кемпе может потерпеть неудачу для этого графика. На рисунке смежности между областями этой карты образуют граф Эррера, частично четырехцветный с неокрашенной внешней областью. Ошибочное доказательство Кемпе следует идее расширения частичных раскрасок, таких как эта, путем перекраски Цепи кемпе, связанные подграфы, имеющие только два цвета. Любую такую цепочку можно перекрасить, сохранив правильность раскраски, поменяв местами два ее цвета на всех вершинах цепи. Доказательство Кемпе имеет разные случаи в зависимости от того, имеет ли следующая раскрашиваемая вершина трех, четырех или пяти соседей и от как окрашены эти соседи. В показанном случае следующей будет окрашена вершина, соответствующая внешней области карты. Эту область нельзя раскрасить напрямую, потому что у нее уже есть соседи всех четырех разных цветов. Синие и желтые соседи соединены одной цепочкой Кемпе (показаны пунктирными желтыми линиями на изображении), что предотвращает превращение их обоих в синий или оба желтых и освобождает цвет. еще одна цепочка Кемпе (пунктирные зеленые линии). В таком случае доказательство Кемпе будет пытаться одновременно поменять местами цвета двух цепочек Кемпе, левой красно-желтой цепочки и правой красно-зеленой цепочки (пунктирные красные линии). Сине-зеленая цепочка блокирует левую красно-желтую цепочку. от достижения правой стороны графика, а сине-желтая цепочка блокирует правую красно-зеленую цепочку от достижения левой, поэтому может показаться, что одновременная перестановка цветов в этих двух цепочках - безопасная операция. желтые и сине-зеленые цепи пересекают друг друга, а не остаются разделенными, в середине рисунка есть область, где могут встречаться красно-желтые и красно-зеленые цепи. Когда эти две цепи встречаются в середине, происходит одновременный обмен местами. смежные желтые и зеленые вершины в этой средней области (например, вершины, представленные верхними желтыми и зелеными областями на рисунке) становятся красными, что приводит к недопустимой окраске.
Приложения в химии
Химическая теория графов касается теоретико-графовой структуры молекулы и другие кластеры атомов. И сам граф Эрреры, и его двойственный граф актуальны в этом контексте.
Атомы металлы Такие как золото может сформировать кластеры в котором центральный атом окружен еще двенадцатью атомами по образцу икосаэдр. Другой, более крупный тип кластера может быть сформирован путем объединения двух из этих икосаэдрических кластеров, так что центральный атом каждого кластера становится одним из граничных атомов для другого кластера. В результате кластер из 19 атомов имеет два внутренних атома (центры двух икосаэдров) с 17 атомами во внешней оболочке в образце графа Эррера.[4]
В двойственный граф графа Эрреры является фуллерен[1] с 30 вершинами, обозначенные в химической литературе как C30(D5час)[5] или F30(D5час)[6] чтобы указать на его симметрию и отличить его от других 30-вершинных фуллеренов. Эта форма также играет центральную роль в создании многомерных фуллеренов.[6]
Рекомендации
- ^ а б c d Хатчинсон, Джоан; Вагон, Стан (1998), "Повторное посещение Кемпе", Американский математический ежемесячный журнал, 105 (2): 170–174, Дои:10.2307/2589650, МИСТЕР 1605875.
- ^ Эррера, А. (1921), Du coloriage des cartes et de quelques questions d'analysis situs, Кандидат наук. Тезис.
- ^ Гетнер, Эллен; Спрингер, Уильям М., II (2003 г.), «Насколько ложно доказательство Кемпе теоремы о четырех цветах?», Труды Тридцать четвертой Юго-Восточной международной конференции по комбинаторике, теории графов и вычислениям, Congressus Numerantium, 164: 159–175, МИСТЕР 2050581.
- ^ Майкл, Д .; Мингос, П. (2015), "Структурные и связывающие узоры в кластерах золота", Dalton Trans., 44 (15): 6680–6695, Дои:10.1039 / c5dt00253b.
- ^ Матур, Ракеш Бехари; Сингх, Бхану Пратап; Панде, Шайладжа (2016), Углеродные наноматериалы: синтез, структура, свойства и применение, CRC Press, стр. 59, ISBN 9781498702119.
- ^ а б Деза, Мишель; Штогрин, Михаил (1999), "Трех-, четырех- и пятимерные фуллерены", Бюллетень математики Юго-Восточной Азии, 23 (1): 9–18, arXiv:математика / 9906035, Bibcode:1999математика ...... 6035D, МИСТЕР 1810781.



