WikiDer > Удержание первого порядка

Удержание первого порядка (FOH) представляет собой математическую модель практического восстановления дискретизированных сигналов, которое может быть выполнено обычным цифро-аналоговый преобразователь (DAC) и аналоговая схема называется интегратор. Для FOH сигнал реконструируется как кусочно-линейный приближение к исходному сигналу, который был выбран. Математическая модель, такая как FOH (или, чаще, удержание нулевого порядка) необходимо, потому что в теорема выборки и реконструкции, последовательность Импульсы Дирака, Икс_s(т), представляющие собой дискретные выборки, Икс(нТл), является фильтр нижних частот чтобы восстановить исходный сигнал, который был выбран, Икс(т). Однако вывод последовательности импульсов Дирака нецелесообразен. Устройства могут быть реализованы с использованием обычного ЦАП и некоторой линейной аналоговой схемы для восстановления кусочно-линейного выхода либо для прогнозирующего, либо для FOH с задержкой.

Хотя это нет то, что делается физически, идентичный выходной сигнал может быть получен путем применения гипотетической последовательности импульсов Дирака, Икс_s(т), к линейная инвариантная во времени система, иначе известный как линейный фильтр с такими характеристиками (которые для LTI-системы полностью описываются импульсивный ответ), так что каждый входной импульс приводит к правильной кусочно-линейной функции на выходе.

Базовое удержание первого порядка

Идеально дискретизированный сигнал Икс_s(т).

Удержание первого порядка - это гипотетический фильтр или же Система LTI который преобразует идеально дискретизированный сигнал

${ Displaystyle х_ {s} (т) ,}$	${ Displaystyle = Икс (Т) Т сумма _ {п = - infty} ^ { infty} дельта (т-нТ) }$
	${ displaystyle = T sum _ {n = - infty} ^ { infty} x (nT) delta (t-nT) }$

Кусочно-линейный сигнал Икс_FOH(т).

к кусочно-линейному сигналу

${ displaystyle x _ { mathrm {FOH}} (t) , = sum _ {n = - infty} ^ { infty} x (nT) mathrm {tri} left ({ frac {t- nT} {T}} right) }$

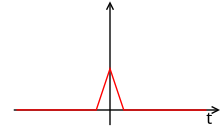
Импульсная характеристика (непричинная) удержания первого порядка час_FOH(т).

что привело к эффективному импульсивный ответ из

${ displaystyle h _ { mathrm {FOH}} (t) , = { frac {1} {T}} mathrm {tri} left ({ frac {t} {T}} right) = { begin {cases} { frac {1} {T}} left (1 - { frac {| t |} {T}} right) & { mbox {if}} | t |$

куда ${ Displaystyle mathrm {три} (х) }$ это треугольная функция.

Эффективная частотная характеристика - это непрерывное преобразование Фурье импульсной характеристики.

${ Displaystyle Н _ { mathrm {FOH}} (е) ,}$	${ Displaystyle = { mathcal {F}} {ч _ { mathrm {FOH}} (т) } }$
	${ displaystyle = left ({ frac {e ^ {i pi fT} -e ^ {- i pi fT}} {i2 pi fT}} right) ^ {2} }$
	${ displaystyle = mathrm {sinc} ^ {2} (fT) }$

куда ${ displaystyle mathrm {sinc} (x) = { frac { sin ( pi x)} { pi x}} }$ нормализованный функция sinc.

В Преобразование Лапласа функция передачи FOH находится заменой s = я 2 π ж:

${ Displaystyle H _ { mathrm {FOH}} (s) ,}$	${ Displaystyle = { mathcal {L}} {ч _ { mathrm {FOH}} (т) } }$
	${ displaystyle = left ({ гидроразрыва {е ^ {sT / 2} -e ^ {- sT / 2}} {sT}} right) ^ {2} }$

Это акаузальная система в том, что функция линейной интерполяции перемещается к значению следующей выборки до того, как такая выборка будет применена к гипотетическому фильтру FOH.

Отложенное удержание первого порядка

Кусочно-линейный сигнал с задержкой Икс_FOH(т).

Отложенное удержание первого порядкаиногда называют причинное удержание первого порядка, идентичен FOH выше, за исключением того, что его вывод задерживается на один период выборки приводящий к задержанному кусочно-линейному выходному сигналу

${ displaystyle x _ { mathrm {FOH}} (t) , = sum _ {n = - infty} ^ { infty} x (nT) mathrm {tri} left ({ frac {tT- nT} {T}} right) }$

Импульсный отклик причинного удержания первого порядка час_FOH(т).

что привело к эффективному импульсивный ответ из

${ displaystyle h _ { mathrm {FOH}} (t) , = { frac {1} {T}} mathrm {tri} left ({ frac {tT} {T}} right) = { begin {cases} { frac {1} {T}} left (1 - { frac {| tT |} {T}} right) & { mbox {if}} | tT |$

куда ${ Displaystyle mathrm {три} (х) }$ это треугольная функция.

Эффективная частотная характеристика - это непрерывное преобразование Фурье импульсной характеристики.

${ Displaystyle Н _ { mathrm {FOH}} (е) ,}$	${ Displaystyle = { mathcal {F}} {ч _ { mathrm {FOH}} (т) } }$
	${ displaystyle = left ({ frac {1-e ^ {- i2 pi fT}} {i2 pi fT}} right) ^ {2} }$
	${ Displaystyle = е ^ {- i2 pi fT} mathrm {sinc} ^ {2} (fT) }$

куда ${ Displaystyle mathrm {sinc} (х) }$ это функция sinc.

В Преобразование Лапласа функция передачи задержанного FOH находится заменой s = я 2 π ж:

${ Displaystyle H _ { mathrm {FOH}} (s) ,}$	${ Displaystyle = { mathcal {L}} {ч _ { mathrm {FOH}} (т) } }$
	${ displaystyle = left ({ frac {1-e ^ {- sT}} {sT}} right) ^ {2} }$

Задержанный вывод делает это причинная система. Импульсный отклик FOH с задержкой не реагирует раньше входного импульса.

Этот вид отсроченной кусочно-линейной реконструкции физически реализуем путем реализации цифровой фильтр выгоды ЧАС(z) = 1 − z⁻¹, применяя выходной сигнал этого цифрового фильтра (который просто Икс[п]−Икс[п−1]) к идеальному условному цифро-аналоговый преобразователь (который имеет присущее удержание нулевого порядка в качестве своей модели) и интегрирующей (в непрерывном времени, ЧАС(s) = 1/(СТ)) выход ЦАП.

Прогнозируемое удержание первого порядка

Прогнозирующий выходной сигнал FOH Икс_FOH(т).

Наконец, прогнозируемое удержание первого порядка совсем другое. Это причинный гипотетическая система LTI или фильтр, преобразующий идеально дискретизированный сигнал

${ Displaystyle х_ {s} (т) ,}$	${ Displaystyle = Икс (Т) Т сумма _ {п = - infty} ^ { infty} дельта (т-нТ) }$
	${ displaystyle = T sum _ {n = - infty} ^ { infty} x (nT) delta (t-nT) }$

в кусочно-линейный выход, так что текущая выборка и непосредственно предыдущая выборка используются для линейного экстраполировать до следующего экземпляра выборки. Выход такого фильтра будет

${ Displaystyle х _ { mathrm {FOH}} (т) ,}$	${ displaystyle = sum _ {n = - infty} ^ { infty} left (x (nT) + left (x (nT) -x ((n-1) T) right) { frac {t-nT} {T}} right) mathrm {rect} left ({ frac {t-nT} {T}} - { frac {1} {2}} right) }$
	${ displaystyle = sum _ {n = - infty} ^ { infty} x (nT) left ( mathrm {rect} left ({ frac {t-nT} {T}} - { frac {1} {2}} right) - mathrm {rect} left ({ frac {t-nT} {T}} - { frac {3} {2}} right) + mathrm {tri } left ({ frac {t-nT} {T}} - 1 right) right) }$

Импульсная характеристика прогнозируемого удержания первого порядка час_FOH(т).

что привело к эффективному импульсивный ответ из

${ Displaystyle ч _ { mathrm {FOH}} (т) ,}$	${ displaystyle = { frac {1} {T}} left ( mathrm {rect} left ({ frac {t} {T}} - { frac {1} {2}} right) - mathrm {rect} left ({ frac {t} {T}} - { frac {3} {2}} right) + mathrm {tri} left ({ frac {t} {T} } -1 вправо) вправо) }$
	${ displaystyle = { begin {case} { frac {1} {T}} left (1 + { frac {t} {T}} right) & { mbox {if}} 0 leq t$

куда ${ Displaystyle mathrm {rect} (х) }$ это прямоугольная функция и ${ Displaystyle mathrm {три} (х) }$ это треугольная функция.

Эффективная частотная характеристика - это непрерывное преобразование Фурье импульсной характеристики.

${ Displaystyle Н _ { mathrm {FOH}} (е) ,}$	${ Displaystyle = { mathcal {F}} {ч _ { mathrm {FOH}} (т) } }$
	${ displaystyle = (1 + i2 pi fT) left ({ frac {1-e ^ {- i2 pi fT}} {i2 pi fT}} right) ^ {2} }$
	${ displaystyle = (1 + i2 pi fT) e ^ {- i2 pi fT} mathrm {sinc} ^ {2} (fT)) }$

куда ${ Displaystyle mathrm {sinc} (х) }$ это функция sinc.

В Преобразование Лапласа функция передачи прогнозируемого FOH находится путем замены s = я 2 π ж:

${ Displaystyle H _ { mathrm {FOH}} (s) ,}$	${ Displaystyle = { mathcal {L}} {ч _ { mathrm {FOH}} (т) } }$
	${ displaystyle = (1 + sT) left ({ frac {1-e ^ {- sT}} {sT}} right) ^ {2} }$

Это причинная система. Импульсная характеристика прогнозирующего FOH не реагирует до входного импульса.

Такая кусочно-линейная реконструкция физически реализуема, если реализовать цифровой фильтр выгоды ЧАС(z) = 1 − z⁻¹, применяя выходной сигнал этого цифрового фильтра (который просто Икс[п]−Икс[п−1]) к идеальному условному цифро-аналоговый преобразователь (который имеет присущее удержание нулевого порядка в качестве модели) и применяя этот выход ЦАП к аналоговому фильтру с передаточной функцией ЧАС(s) = (1+СТ)/(СТ).

Смотрите также

• Теорема выборки Найквиста – Шеннона
• Удержание нулевого порядка
• Билинейная интерполяция

внешняя ссылка

• Удержание нулевого порядка и интерполяция на основе удержания первого порядка