WikiDer > График Франклина - Википедия

График Франклина
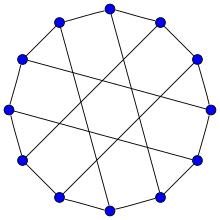График Франклина
Названный в честь	Филип Франклин
Вершины	12
Края	18
Радиус	3
Диаметр	3
Обхват	4
Автоморфизмы	48 (Z/2Z×S4)
Хроматическое число	2
Хроматический индекс	3
Род	1
Характеристики	Кубический Гамильтониан Двудольный Без треугольников Идеально Вершинно-транзитивный
Таблица графиков и параметров

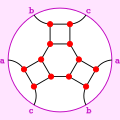
в математический поле теория графов, то Граф Франклина это 3-регулярный граф с 12 вершинами и 18 ребрами.^[1]

Граф Франклина назван в честь Филип Франклин, который опроверг Гипотеза Хивуда от количества цветов, необходимых при разбиении двумерной поверхности на ячейки вложение графа.^[2][3] Гипотеза Хивуда подразумевает, что максимальное хроматическое число отображения на Бутылка Клейна должно быть семь, но Франклин доказал, что в этом случае всегда достаточно шести цветов. Граф Франклина может быть встроен в бутылку Клейна, так что он формирует карту, требующую шести цветов, показывая, что в этом случае иногда необходимо шесть цветов. Это вложение является Петри двойной его вложения в проективная плоскость показано ниже.

это Гамильтониан и имеет хроматическое число 2, хроматический индекс 3, радиус 3, диаметр 3 и обхват 4. Это также 3-вершинно-связанный и 3-реберный идеальный график.

Алгебраические свойства

В группа автоморфизмов графа Франклина имеет порядок 48 и изоморфен Z/2Z×S₄, то прямой продукт из циклическая группа Z/2Z и симметричная группа S₄. Он действует транзитивно на вершинах графа, делая его вершинно-транзитивный.

В характеристический многочлен графа Франклина

${ displaystyle (x-3) (x-1) ^ {3} (x + 1) ^ {3} (x + 3) (x ^ {2} -3) ^ {2}. }$

Галерея

• 

  В хроматическое число графа Франклина равно 2.

• 

  В хроматический индекс графа Франклина равно 3.

• 

  Альтернативный рисунок графа Франклина.

• 

  Граф Франклина, вложенный в проективную плоскость, как усеченный полуоктаэдр.

Викискладе есть медиафайлы по теме Граф Франклина.

Рекомендации