WikiDer > Гауссовский логарифм

В математике логарифмы сложения и вычитания или же Гауссовские логарифмы можно использовать, чтобы найти логарифмы из сумма и разница пары значений, логарифмы которых известны, не зная самих значений.^[1]

Их математические основы восходят к Зеккини Леонелли^[2][3] и Карл Фридрих Гаусс^[4][1][5] в начале 1800-х гг.^{[2][3][4][1][5]}

В ${displaystyle s_ {b} (z)}$ и ${displaystyle d_ {b} (z)}$ функции для ${displaystyle b = e}$.

Операции сложения и вычитания можно рассчитать по формуле:

${displaystyle log _ {b} (| X | + | Y |) = x + s_ {b} (y-x)}$

${displaystyle log _ {b} (|| X | - | Y ||) = x + d_ {b} (y-x),}$

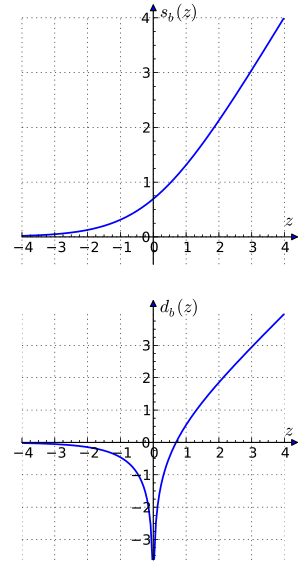
где функция "сумма" определяется как ${displaystyle s_ {b} (z) = log _ {b} (1 + b ^ {z})}$, а функция "разница" - ${displaystyle d_ {b} (z) = log _ {b} (| 1-b ^ {z} |)}$. Функции ${displaystyle s_ {b} (z)}$ и ${displaystyle d_ {b} (z)}$ также известны как Гауссовские логарифмы.

За натуральные логарифмы с ${displaystyle b = e}$ следующие тождества с гиперболические функции существовать:

${displaystyle s_ {e} (z) = ln 2+ {frac {z} {2}} + ln left (cosh {frac {z} {2}} ight)}$

${displaystyle d_ {e} (z) = ln 2+ {frac {z} {2}} + ln left | sinh {frac {z} {2}} ight |}$

Это показывает, что ${displaystyle s_ {e}}$ имеет Расширение Тейлора где все члены, кроме первого, являются рациональными, а все нечетные члены, кроме линейного, равны нулю.

Упрощение умножения, деления, корней и степеней уравновешивается стоимостью оценки этих функций для сложения и вычитания.

Смотрите также

• Softplus операция в нейронные сети
• Логарифм Зеха
• Таблица логарифмов
• Логарифмическая система счисления (LNS)

Рекомендации

дальнейшее чтение

• Старк, Брюс Д. (1997) [1995]. Таблицы Старка для определения лунного расстояния и определения всемирного времени с помощью наблюдения секстанта, включая удобный способ отточить навыки астрономической навигации на суше (2-е изд.). Публикации Starpath. ISBN 978-0914025214. 091402521X. Получено 2015-12-02. (NB. Содержит таблицу гауссовых логарифмов LG(1+10^-Икс).)
• Каливода, янв (30.07.2003). "Брюс Старк - Таблицы для определения лунного расстояния и поиска G.M.T. с помощью Sextant Observation (1995, 1997)" (Рассмотрение). Прага, Чешская Республика. В архиве из оригинала 12.01.2004. Получено 2015-12-02. …] Брюс Старк […] использует гауссовские логарифмы, которые позволяют оставаться в мире логарифмов все время вычислений и преобразует сложение натуральных чисел в сложение и вычитание их общих и специальных логарифмических значений с помощью специальной таблицы . Это намного проще, чем преобразовывать журналы в их естественные значения, добавлять их и снова преобразовывать в журналы. Более того, гауссовы логарифмы дают более точный результат, чем традиционный метод вычислений, и помогают 5-значным логарифмам быть достаточно точными для этого метода. […] Использование Брюсом «гауссиан» является оригинальным в области навигации. Я не знаю другого примера их использования моряками или авиаторами - за исключением советских штурманов, у которых в стандартных наборах таблиц были гауссианы до ок. 1960. […] гаверсин это было недопустимо в советской навигационной практике. […] Гауссианцы мирно сотрудничают с гаванью в рационализации LD процедура […] [1][2]
• Кремер, Герман (2002-08-29). "Gauss'sche Additionslogarithmen feiern 200. Geburtstag". de.sci.mathematik (на немецком). В архиве из оригинала на 2018-07-07. Получено 2018-07-07.
• Кюн, Клаус (2008). "C. F. Gauß und die Logarithmen" (PDF) (на немецком). Аллинг-Бибург, Германия. В архиве (PDF) из оригинала на 2018-07-14. Получено 2018-07-14.