WikiDer > Код Грея
| Lucal код[1][2] | |||||
|---|---|---|---|---|---|
| 5 | 4 | 3 | 2 | 1 | |
| Код Грея | |||||
| 4 | 3 | 2 | 1 | ||
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 1 | 0 |
| 3 | 0 | 0 | 1 | 0 | 1 |
| 4 | 0 | 1 | 1 | 0 | 0 |
| 5 | 0 | 1 | 1 | 1 | 1 |
| 6 | 0 | 1 | 0 | 1 | 0 |
| 7 | 0 | 1 | 0 | 0 | 1 |
| 8 | 1 | 1 | 0 | 0 | 0 |
| 9 | 1 | 1 | 0 | 1 | 1 |
| 10 | 1 | 1 | 1 | 1 | 0 |
| 11 | 1 | 1 | 1 | 0 | 1 |
| 12 | 1 | 0 | 1 | 0 | 0 |
| 13 | 1 | 0 | 1 | 1 | 1 |
| 14 | 1 | 0 | 0 | 1 | 0 |
| 15 | 1 | 0 | 0 | 0 | 1 |
В отраженный двоичный код (РБК), также известный как отраженный двоичный (РБ) или же Код Грея после Фрэнк Грей, это порядок двоичная система счисления такие, что два последовательных значения отличаются только одним кусочек (двоичный символ).
Например, представление десятичного значения «1» в двоичном формате обычно будет «001», а «2» будет «010». В коде Грея эти значения представлены как «001» и «011». Таким образом, для увеличения значения с 1 до 2 потребуется изменить только один бит вместо двух.
Коды Грея широко используются для предотвращения ложного вывода электромеханический переключатели и облегчить исправление ошибки в цифровых коммуникациях, таких как цифровое наземное телевидение и немного Кабельное ТВ системы.
Имя
Bell Labs Исследователь Фрэнк Грей ввел термин отраженный двоичный код в своей патентной заявке 1947 года, отмечая, что у кода «пока нет признанного названия».[3] Он получил свое название от того факта, что он «может быть построен из обычного двоичного кода посредством своего рода процесса отражения».
Код был позже назван в честь Грея другими, кто его использовал. Две разные патентные заявки 1953 года используют «код Грея» в качестве альтернативного названия «отраженного двоичного кода»;[4][5] в одном из них также указаны «минимальный код ошибки» и «код циклической перестановки» среди имен.[5] В заявке на патент 1954 года упоминается «код Грея по телефону Bell».[6] Другие названия включают «циклический двоичный код», «код циклической прогрессии»,[7][8] "циклическая перестановка двоичного кода"[9] или «циклический переставленный двоичный код» (CPB).[10][11]
Мотивация
Многие устройства указывают положение, замыкая и размыкая переключатели. Если это устройство использует естественные двоичные коды, позиции 3 и 4 расположены рядом друг с другом, но все три бита двоичного представления различаются:
| Десятичный | Двоичный |
|---|---|
| ... | ... |
| 3 | 011 |
| 4 | 100 |
| ... | ... |
Проблема с естественными двоичными кодами заключается в том, что физические переключатели не идеальны: очень маловероятно, что физические переключатели будут изменять состояния точно синхронно. При переходе между двумя показанными выше состояниями все три переключателя изменяют состояние. За короткий период, пока все меняется, переключатели будут считывать какое-то ложное положение. Даже без keybounce, переход может выглядеть как 011 - 001 - 101 - 100. Когда переключатели оказываются в положении 001, наблюдатель не может сказать, является ли это «реальным» положением 001 или переходным состоянием между двумя другими положениями. Если вывод подается в последовательный система, возможно через комбинационная логика, то последовательная система может сохранить ложное значение.
Отраженный двоичный код решает эту проблему, изменяя только один переключатель за раз, поэтому нет двусмысленности положения:
| Десятичный | Двоичный | серый |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| 11 | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| 15 | 1111 | 1000 |
Код Грея для десятичного числа 15 переключается на десятичный 0 с одним переключением переключателя. Это называется «циклическим» свойством кода Грея. В стандартном кодировании Грея младший значащий бит следует повторяющейся схеме: 2 вкл., 2 выкл. ( … 11001100 … ); следующая цифра - образец 4 вкл., 4 выкл .; n-й младший бит шаблон на выключенный.
Более формально Код Грея это код, присваивающий каждому из непрерывного набора целые числаили для каждого члена кругового списка - слово символов, такое, что никакие два кодовых слова не являются идентичными, а каждые два соседних кодовых слова отличаются ровно на один символ. Эти коды также известны как единичное расстояние,[12][13][14][8][15][16] на одно расстояние, один шаг, монострофический[17][18][15][16] или же синкопические коды,[17] в отношении Расстояние Хэмминга 1 между соседними кодами. В принципе, для данной длины слова может быть более одного такого кода, но термин «код Грея» впервые был применен к конкретному двоичный код для неотрицательных целых чисел, двоично-отраженный код Грея, или же BRGC, четырехбитная версия которого показана выше.
История и практическое применение
Отраженные двоичные коды применялись к математическим головоломкам еще до того, как они стали известны инженерам. Мартин Гарднер написал популярный отчет о коде Грея в августе 1972 г. Колонка "Математические игры" в журнале Scientific American. Французский инженер Эмиль Бодо использовали коды Грея в телеграфия в 1878 г.[19] Он получил французский Почетный легион медаль за свою работу. Код Грея иногда неправильно приписывают[20] к Элиша Грей.[21][22][23]
Фрэнк Грей, который прославился изобретением метода передачи сигналов, который стал использоваться для совместимого цветного телевидения, изобрел метод преобразования аналоговых сигналов в группы отраженного двоичного кода с использованием вакуумная трубана базе аппарата. Метод и устройство были запатентованы в 1953 году, и имя Грея закрепилось за кодами. "Трубка PCM«Аппарат, который запатентовал Грей, был создан Рэймондом У. Сирсом из Bell Labs в сотрудничестве с Греем и Уильямом М. Гудоллом, которые приписывали Грею идею отраженного двоичного кода.[24]
Грея больше всего интересовало использование кодов для минимизации ошибок преобразования аналоговых сигналов в цифровые; его коды до сих пор используются для этой цели.
Датчики положения

Коды Грея используются в линейных и поворотных датчиках положения (абсолютные энкодеры и квадратурные энкодеры) вместо взвешенного двоичного кодирования. Это исключает возможность того, что при изменении нескольких битов в двоичном представлении позиции неправильное чтение будет результатом того, что некоторые биты изменятся раньше других.
Например, некоторые поворотные энкодеры предоставляют диск, на концентрических кольцах (дорожках) которого нанесен электропроводящий код Грея. Каждая дорожка имеет неподвижный металлический пружинный контакт, который обеспечивает электрический контакт с проводящим шаблоном кода. Вместе эти контакты создают выходные сигналы в виде кода Грея. В других кодерах используются бесконтактные механизмы на основе оптических или магнитных датчиков для создания выходных сигналов кода Грея.
Независимо от механизма или точности движущегося энкодера, ошибка измерения положения может возникать в определенных положениях (на границах кода), поскольку код может изменяться в тот самый момент, когда он считывается (дискретизируется). Двоичный выходной код может вызвать значительные ошибки измерения положения, поскольку невозможно изменить все биты в одно и то же время. Если в момент выборки позиции некоторые биты изменились, а другие нет, позиция выборки будет неправильной. В случае абсолютных энкодеров указанное положение может быть далеко от фактического положения, а в случае инкрементальных энкодеров это может нарушить отслеживание положения.
Напротив, код Грея, используемый датчиками положения, гарантирует, что коды для любых двух последовательных положений будут отличаться только на один бит, и, следовательно, только один бит может изменяться за раз. В этом случае максимальная ошибка положения будет небольшой, указывая на положение, смежное с фактическим положением.
Математические головоломки
Код Грея, отраженный двоичным кодом, может служить руководством для решения Башни ханойской проблемы, а также классический Пазл китайские кольца, последовательный механический механизм головоломки.[20] Он также образует Гамильтонов цикл на гиперкуб, где каждый бит рассматривается как одно измерение.
Генетические алгоритмы
Из-за Расстояние Хэмминга свойств кодов Грея, они иногда используются в генетические алгоритмы. Они очень полезны в этой области, поскольку мутации в коде позволяют вносить в основном инкрементные изменения, но иногда изменение одного бита может вызвать большой скачок и привести к новым свойствам.
Минимизация логической схемы
Коды Грея также используются при маркировке осей Карты Карно[25][26] а также в Круговые графы Хендлера,[27][28][29][30] оба графических метода для минимизация логической схемы.
Исправление ошибки
В современном цифровые коммуникации, Коды Грея играют важную роль в исправление ошибки. Например, в цифровая модуляция схема, такая как QAM где данные обычно передаются в символы 4 бит или более, сигнал диаграмма созвездия устроен так, что битовые комбинации, передаваемые соседними точками совокупности, отличаются только на один бит. Объединив это с упреждающее исправление ошибок способный исправлять однобитовые ошибки, возможно приемник для исправления любых ошибок передачи, которые вызывают отклонение точки созвездия в область соседней точки. Это делает систему передачи менее восприимчивой к шум.
Связь между доменами часов
Разработчики цифровой логики широко используют коды Грея для передачи многобитовой информации счетчика между синхронной логикой, которая работает на разных тактовых частотах. Считается, что логика работает в разных «тактовых областях». Это фундаментально для дизайна больших микросхем, которые работают с множеством разных тактовых частот.
Циклическое переключение состояний с минимальными усилиями
Если системе необходимо циклически перебрать все возможные комбинации состояний включения-выключения некоторого набора элементов управления, а изменение элементов управления требует нетривиальных затрат (например, время, износ, человеческая работа), код Грея минимизирует количество настроек. изменяется только на одно изменение для каждой комбинации состояний. Примером может служить тестирование системы трубопроводов на все комбинации настроек клапанов с ручным управлением.
А сбалансированный код Грея могут быть построены,[31] которые переворачиваются одинаково часто. Поскольку перевороты битов распределены равномерно, это оптимально следующим образом: сбалансированные коды Грея минимизируют максимальное количество переворотов битов для каждой цифры.
Счетчики кода Грея и арифметика
Типичное использование счетчиков кода Грея - создание ФИФО (первым пришел - первым вышел) буфер данных, который имеет порты чтения и записи, которые существуют в разных тактовых доменах. Счетчики входов и выходов внутри такого двухпортового FIFO часто хранятся с использованием кода Грея, чтобы предотвратить захват недопустимых переходных состояний, когда счетчик пересекает тактовые области.[32]Обновленные указатели чтения и записи должны передаваться между доменами часов при их изменении, чтобы иметь возможность отслеживать состояние пустого и полного FIFO в каждом домене. Каждый бит указателей выбирается недетерминированно для этой передачи тактовой области. Таким образом, для каждого бита распространяется либо старое значение, либо новое значение. Следовательно, если в точке выборки изменяется более одного бита в многобитовом указателе, «неправильное» двоичное значение (ни новое, ни старое) не может быть передано. Гарантируя возможность изменения только одного бита, коды Грея гарантируют, что единственными возможными значениями выборки являются новое или старое многобитовое значение. Обычно используются коды Грея с длиной степени двойки.
Иногда цифровые шины в электронных системах используются для передачи величин, которые могут увеличиваться или уменьшаться только по одному за раз, например, выходной сигнал счетчика событий, который передается между доменами часов или на цифро-аналоговый преобразователь. Преимущество кодов Грея в этих приложениях состоит в том, что различия в задержках распространения множества проводов, которые представляют биты кода, не могут привести к тому, что полученное значение пройдет через состояния, которые находятся вне последовательности кода Грея. Это похоже на преимущество кодов Грея в конструкции механических энкодеров, однако источником кода Грея в этом случае является электронный счетчик. Сам счетчик должен вести счет в коде Грея, или, если счетчик работает в двоичном формате, то выходное значение счетчика должно быть повторно синхронизировано после преобразования в код Грея, потому что при преобразовании значения из двоичного кода в код Грея,[nb 1] возможно, что различия во времени поступления битов двоичных данных в схему преобразования двоичного кода в серый будут означать, что код может на короткое время пройти через состояния, которые сильно не соответствуют последовательности. Добавление синхронизированного регистра после схемы, которая преобразует значение счетчика в код Грея, может привести к тактовому циклу задержки, поэтому прямой счет в коде Грея может быть полезным.[33]
Чтобы произвести следующее значение счетчика в счетчике кода Грея, необходимо иметь некоторую комбинационную логику, которая будет увеличивать текущее сохраненное значение счетчика. Один из способов увеличения числа кода Грея - преобразовать его в обычный двоичный код, добавить к нему единицу с помощью стандартного двоичного сумматора, а затем преобразовать результат обратно в код Грея.[34] Другие методы подсчета в коде Грея обсуждаются в отчете Роберт В. Доран, включая получение выходных данных с первых защелок триггеров ведущий-ведомый в двоичный счетчик пульсаций.[35]
Адресация кода Грея
Как исполнение программный код обычно вызывает шаблон доступа к памяти команд локально последовательных адресов, кодировки автобусов использование адресации кода Грея вместо двоичной адресации может значительно уменьшить количество изменений состояния битов адреса, тем самым уменьшая Потребляемая мощность процессора в некоторых маломощных конструкциях.[36][37]
Строительство п-битовый код Грея
Список двоичных кодов Грея для п биты могут быть сгенерированы рекурсивно из списка для п - 1 бит, отражая список (то есть перечисляя записи в обратном порядке), добавляя к записям в исходном списке префикс двоичного 0, добавляя к записям в отраженном списке двоичную единицу, а затем конкатенируя исходный список с обратным список.[20] Например, создание п = 3 список из п = 2 список:
| 2-битный список: | 00, 01, 11, 10 | |
| Отражено: | 10, 11, 01, 00 | |
| Префикс старых записей с 0: | 000, 001, 011, 010, | |
| Добавляйте к новым записям префикс 1: | 110, 111, 101, 100 | |
| Составные: | 000, 001, 011, 010, | 110, 111, 101, 100 |
Однобитовый код Грея грамм1 = (0, 1). Это можно представить как построенное рекурсивно, как указано выше, из нулевого битового кода Грея. грамм0 = ( Λ ), состоящий из единственной записи нулевой длины. Этот итеративный процесс создания граммп+1 из граммп проясняет следующие свойства стандартного отражающего кода:
- граммп это перестановка чисел 0,…, 2п - 1. (Каждое число появляется в списке ровно один раз.)
- граммп встроена как первая половина граммп+1.
- Следовательно, кодировка стабильный, в том смысле, что как только двоичное число появляется в граммп он отображается в том же месте во всех более длинных списках; так что имеет смысл поговорить о то отражающий код Грея значение числа: грамм(м) = м-й отражающий код Грея, считая от 0.
- Каждая запись в граммп отличается от предыдущей записи всего на один бит. (Расстояние Хэмминга равно 1.)
- Последняя запись в граммп отличается от первой записи всего на один бит. (Код циклический.)
Эти характеристики предлагают простой и быстрый метод преобразования двоичного значения в соответствующий код Грея. Каждый бит инвертируется, если следующий старший бит входного значения установлен в единицу. Это может выполняться параллельно с помощью битового сдвига и операции исключающее ИЛИ, если они доступны: п-й код Грея получается путем вычисления . Добавление 0 оставляет порядок кодовых слов неизменным, а добавление 1 меняет порядок кодовых слов на обратный. Если биты в позиции кодовых слов инвертируются, порядок соседних блоков кодовые слова перевернуты. Например. если бит 0 инвертируется в 3-битной последовательности кодовых слов, порядок двух соседних кодовых слов меняется на противоположный
{000,001,010,011,100,101,110,111} -> {001,000,011,010,101,100,111,110} (инвертировать бит 0)
Если бит 1 инвертирован, блоки из 2 кодовых слов изменяют порядок:
{000,001,010,011,100,101,110,111} -> {010,011,000,001,110,111,100,101} (инвертировать бит 1)
Если бит 2 инвертирован, блоки из 4 кодовых слов меняют порядок:
{000,001,010,011,100,101,110,111} -> {100,101,110,111,000,001,010,011} (инвертировать бит 2)
Таким образом, немного оторвавшись на позиции с битой на позиции оставляет порядок кодовых слов нетронутым, если , и меняет порядок блоков кодовые слова, если . Теперь это точно такая же операция, что и метод отражения и префикса для генерации кода Грея.
Аналогичный метод можно использовать для выполнения обратного преобразования, но вычисление каждого бита зависит от вычисленного значения следующего более высокого бита, поэтому его нельзя выполнять параллельно. Предполагая это th Бит с кодировкой Грея ( самый старший бит), и это -й двоично-кодированный бит ( является старшим битом), обратный перевод может быть дан рекурсивно: , и . В качестве альтернативы декодирование кода Грея в двоичное число можно описать как сумма префикса битов в коде Грея, где каждая отдельная операция суммирования в префиксной сумме выполняется по модулю два.
Чтобы итеративно построить двоично-отраженный код Грея, на шаге 0 начните с , а на шаге найти битовую позицию наименее значащей 1 в двоичном представлении и переверните бит в этой позиции в предыдущем коде чтобы получить следующий код . Позиции битов начинаются с 0, 1, 0, 2, 0, 1, 0, 3,….[nb 2] Видеть найти первый набор для эффективных алгоритмов вычисления этих значений.
Преобразование в код Грея и обратно
Следующие функции в C преобразование между двоичными числами и связанными с ними кодами Грея. Хотя может показаться, что преобразование Грея в двоичное требует, чтобы каждый бит обрабатывался по отдельности, существуют более быстрые алгоритмы.[38][nb 1]
typedef беззнаковый int uint;// Эта функция преобразует двоичное число без знака в отраженный двоичный код Грея.uint BinaryToGray(uint число){ возвращаться число ^ (число >> 1); // Оператор >> сдвиг вправо. Оператор ^ исключает или.}// Эта функция преобразует отраженный двоичный код Грея в двоичное число.uint GrayToBinary(uint число){ uint маска = число; пока (маска) { // Каждый бит кода Грея эксклюзивен для всех более значимых битов. маска >>= 1; число ^= маска; } возвращаться число;}// Более эффективная версия для кодов Грея 32 бита или меньше за счет использования методов SWAR (SIMD в регистре). // Он реализует функцию XOR с параллельным префиксом. Операторы присваивания могут быть в любом порядке.// // Эта функция может быть адаптирована для более длинных кодов Грея путем добавления шагов. uint GrayToBinary32(uint число){ число ^= число >> 16; число ^= число >> 8; число ^= число >> 4; число ^= число >> 2; число ^= число >> 1; возвращаться число;}// Вариант «Четыре бита сразу» заменяет двоичное число (abcd) 2 на (abcd) 2 ^ (00ab) 2, затем на (abcd) 2 ^ (00ab) 2 ^ (0abc) 2 ^ (000a) 2.Специальные типы кодов Грея
На практике «код Грея» почти всегда относится к двоично-отраженному коду Грея (BRGC). Однако математики открыли другие виды кодов Грея. Как и BRGC, каждое слово состоит из списка слов, каждое из которых отличается от следующего. только одной цифрой (каждое слово имеет Расстояние Хэмминга из 1 от следующего слова).
п-арный код Грея
|
Помимо двоичного кода Грея, существует множество специализированных типов кодов Грея. Одним из таких типов кода Грея является п-арный код Грея, также известный как не-логический код Грея. Как следует из названия, этот тип кода Грея использует не-Булево значения в его кодировках.
Например, 3-арный (тройной) Код Грея будет использовать значения {0, 1, 2}. (п, k)-Код Грея это п-арный код Грея с k цифры.[39]Последовательность элементов в (3, 2) -сером коде: {00, 01, 02, 12, 11, 10, 20, 21, 22}. (п, k) -Серый код может быть построен рекурсивно, как BRGC, или может быть построен итеративно. An алгоритм итеративно генерировать (N, k) -Серый код представлен (в C):
// входные данные: основание, цифры, значение// вывод: серый// Преобразование значения в код Грея с заданной базой и цифрами.// Итерация по последовательности значений приведет к последовательности// кодов Грея, в которых одновременно изменяется только одна цифра.пустота toGray(беззнаковый основание, беззнаковый цифры, беззнаковый ценить, беззнаковый серый[цифры]){ беззнаковый baseN[цифры]; // Сохраняет обычное число с основанием N, по одной цифре на запись беззнаковый я; // Переменная цикла // Поместите нормальное число baseN в массив baseN. Для базы 10, 109 // будет сохранено как [9,0,1] за (я = 0; я < цифры; я++) { baseN[я] = ценить % основание; ценить = ценить / основание; } // Преобразование нормального числа baseN в эквивалент кода Грея. Обратите внимание, что // цикл начинается со старшей цифры и идет вниз. беззнаковый сдвиг = 0; пока (я--) { // Серая цифра сдвигается вниз на сумму более высоких // цифры. серый[я] = (baseN[я] + сдвиг) % основание; сдвиг = сдвиг + основание - серый[я]; // Вычесть из базы, чтобы сдвиг был положительным }}// ПРИМЕРЫ// ввод: значение = 1899, основание = 10, цифры = 4// вывод: baseN [] = [9,9,8,1], серый [] = [0,1,7,1]// ввод: значение = 1900, основание = 10, цифры = 4// вывод: baseN [] = [0,0,9,1], серый [] = [0,1,8,1]Существуют и другие алгоритмы кода Грея для (п,k) -Серые коды. (п,k) -Серый код, созданный указанным выше алгоритмом, всегда циклический; некоторые алгоритмы, например, Гуан,[39] это свойство отсутствует, когда k нечетное. С другой стороны, хотя с помощью этого метода изменяется только одна цифра за раз, она может измениться путем переноса (цикл от п - от 1 до 0). В алгоритме Гуана счетчик поочередно растет и падает, так что числовая разница между двумя цифрами кода Грея всегда равна единице.
Коды Грея не определены однозначно, поскольку перестановка столбцов такого кода также является кодом Грея. Вышеупомянутая процедура создает код, в котором чем ниже значение цифры, тем чаще она изменяется, что делает его похожим на обычные методы подсчета.
Смотрите также Косая двоичная система счисления, вариантная троичная система счисления, в которой при каждом приращении изменяется не более 2 цифр, так как каждое приращение может быть выполнено не более чем с одной цифрой нести операция.
Сбалансированный код Грея
Хотя двоичный отраженный код Грея полезен во многих сценариях, в некоторых случаях он не является оптимальным из-за отсутствия «единообразия».[31] В сбалансированные коды Грея, количество изменений в разных положениях координат максимально приближено. Чтобы уточнить это, пусть грамм быть р-арный полный цикл Грея с переходной последовательностью ; то количество переходов (спектр) из грамм представляют собой набор целых чисел, определенных
Код Грея униформа или же равномерно сбалансированный если его количество переходов все равно, и в этом случае мы имеем для всех k. Ясно, когда , такие коды существуют, только если п является степенью 2. В противном случае, если п не разделяет равномерно, можно построить хорошо сбалансированный коды, где каждый счетчик переходов либо или же .[31] Коды Грея также могут быть экспоненциально сбалансированный если все их счетчики переходов являются смежными степенями двойки, и такие коды существуют для каждой степени двойки.[40]
Например, сбалансированный 4-битный код Грея имеет 16 переходов, которые могут быть равномерно распределены по всем четырем позициям (четыре перехода на позицию), что делает его равномерно сбалансированным:[31]
0 1 1 1 1 1 1 0 0 0 0 0 0 1 1 0 0 0 1 1 1 1 0 0 1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 1 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 1 1 1 1
тогда как сбалансированный 5-битный код Грея имеет всего 32 перехода, которые не могут быть равномерно распределены по позициям. В этом примере четыре позиции имеют шесть переходов каждая, а одна - восемь:[31]
1 1 1 1 1 0 0 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 1 1 0 0 0 1 1 0 0 1 1 1 0 0 0 0 0 0 1 1 1 0 0 0 1 1 1 1 1 1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 1 1 1 1 1
Сейчас мы покажем конструкцию[41] и реализация[42] для хорошо сбалансированных двоичных кодов Грея, что позволяет нам генерировать п-цифровой сбалансированный код Грея для каждого п. Главный принцип - индуктивно построить (п + 2) -цифровой код Грея учитывая п-цифровой код Грея грамм таким образом, чтобы сохранялось сбалансированное свойство. Для этого рассмотрим перегородки в четное число L непустых блоков формы
куда , и ). Это разбиение индуцирует -цифровой код Грея, заданный
Если мы определим кратности переходов быть количеством раз цифра в позиции я меняется между последовательными блоками в разделе, затем для (п + 2) -значный код Грея, индуцированный этим разбиением переходного спектра является
Тонкая часть этой конструкции - найти адекватное разделение сбалансированного п-цифровой код Грея, такой, что индуцированный им код остается сбалансированным, но для этого имеет значение только кратность переходов; соединение двух последовательных блоков по цифре переход и разделение другого блока на другую цифру переход производит другой код Грея с точно таким же спектром перехода , поэтому можно, например,[40] обозначить первый переходы на цифру как те, что попадают между двумя блоками. Единые коды можно найти, когда и , и эту конструкцию можно распространить на р-часть тоже.[41]
Монотонные коды Грея
Монотонные коды полезны в теории взаимосвязанных сетей, особенно для минимизации расширения линейных массивов процессоров.[43]Если мы определим масса двоичной строки быть числом единиц в строке, то, хотя мы явно не можем иметь код Грея со строго возрастающим весом, мы можем аппроксимировать это, прогнав код через два смежных веса до достижения следующего.
Мы можем формализовать понятие монотонных кодов Грея следующим образом: рассмотрим разбиение гиперкуба в уровни вершин, имеющих одинаковый вес, т.е.
за . Эти уровни удовлетворяют . Позволять быть подграфом индуцированный , и разреши быть краями в . Тогда монотонный код Грея - это гамильтонов путь в так что всякий раз, когда приходит раньше в пути, тогда .
Элегантная конструкция монотонной п-цифровые коды Грея для любых п основан на идее рекурсивного построения подпути длины имея края в .[43] Мы определяем , в любое время или же , и
иначе. Здесь, - подходящим образом определенная перестановка и относится к пути п с его координатами, переставленными на . Эти пути порождают два монотонных п-цифровые коды Грея и данный
Выбор что гарантирует, что эти коды действительно являются кодами Грея, оказывается . Первые несколько значений показаны в таблице ниже.
| j = 0 | j = 1 | j = 2 | j = 3 | |
|---|---|---|---|---|
| п = 1 | 0, 1 | |||
| п = 2 | 00, 01 | 10, 11 | ||
| п = 3 | 000, 001 | 100, 110, 010, 011 | 101, 111 | |
| п = 4 | 0000, 0001 | 1000, 1100, 0100, 0110, 0010, 0011 | 1010, 1011, 1001, 1101, 0101, 0111 | 1110, 1111 |
Эти монотонные коды Грея могут быть эффективно реализованы таким образом, что каждый последующий элемент может быть сгенерирован в О(п) время. Алгоритм проще всего описать с помощью сопрограммы.
Монотонные коды имеют интересную связь с Гипотеза Ловаса, в котором говорится, что каждый подключенный вершинно-транзитивный граф содержит гамильтонов путь. Подграф "среднего уровня" является вершинно-транзитивный (т. е. ее группа автоморфизмов транзитивна, так что каждая вершина имеет одинаковую «локальную среду», и ее нельзя отличить от других, поскольку мы можем переназначить координаты, а также двоичные цифры, чтобы получить автоморфизм), а проблема поиска гамильтонова траектории в этом подграфе называется «проблемой среднего уровня», которая может пролить свет на более общую гипотезу. На вопрос дан положительный ответ для , а предыдущая конструкция для монотонных кодов обеспечивает гамильтонов путь длиной не менее 0,839N куда N - количество вершин в подграфе среднего уровня.[44]
Код Беккета – Грея
Другой тип кода Грея, Код Беккета – Грея, назван в честь ирландского драматурга Сэмюэл Беккет, кто интересовался симметрия. Его игра "Quad"состоит из четырех актеров и разделен на шестнадцать периодов времени. Каждый период заканчивается тем, что один из четырех актеров выходит на сцену или покидает ее. Спектакль начинается с пустой сцены, и Беккет хотел, чтобы каждая подгруппа актеров появлялась на сцене ровно один раз.[45] Очевидно, что набор актеров, которые сейчас находятся на сцене, может быть представлен 4-битным двоичным кодом Грея. Беккет, однако, наложил дополнительное ограничение на сценарий: он хотел, чтобы актеры входили и выходили, чтобы актер, который находился на сцене дольше всех, всегда выходил. Тогда актеров можно было бы представить в виде первым пришел-первым вышел очередь, так что (из актеров на сцене) удаляемый из очереди всегда тот, кто был поставлен в очередь первым.[45] Беккет не смог найти код Беккета – Грея для своей пьесы, и действительно, исчерпывающий список всех возможных последовательностей показывает, что такого кода не существует для п = 4. Сегодня известно, что такие коды существуют для п = 2, 5, 6, 7 и 8 и не существуют для п = 3 или 4. Пример 8-битного кода Беккета – Грея можно найти в Дональд Кнутс Искусство программирования.[20] По словам Савады и Вонга, пространство поиска п = 6 можно изучить за 15 часов, и более 9500 решений для случая п = 7 найдено.[46]
Коды змейки в коробке
Змея в коробке коды, или змеи, - последовательности узлов индуцированные пути в п-размерный граф гиперкуба, и коды катушки в коробке,[47] или же катушки, - последовательности узлов индуцированных циклы в гиперкубе. Рассматриваемые как коды Грея, эти последовательности обладают способностью обнаруживать любую однобитовую ошибку кодирования. Коды этого типа впервые были описаны Уильям Х. Каутц в конце 1950-х гг .;[13] с тех пор было проведено много исследований по поиску кода с максимально возможным количеством кодовых слов для данного измерения гиперкуба.
Однодорожечный код Грея
Еще один вид кода Грея - это однопутный код Грея (STGC) разработан Норманом Б. Спеддингом.[48][49] и усовершенствован Хильтгеном, Патерсоном и Брандестини в «Одноколейных кодах Грея» (1996).[50][51] STGC - это циклический список п уникальное двоичное кодирование длины n, такое, что два последовательных слова отличаются ровно в одной позиции, и когда список рассматривается как п × п матрица, каждый столбец представляет собой циклический сдвиг первого столбца.[52]
Название происходит от их использования с поворотные энкодеры, где несколько дорожек распознаются контактами, в результате чего для каждого на выходе получается 0 или 1. Чтобы уменьшить шум из-за того, что разные контакты не переключаются в один и тот же момент времени, предпочтительно настраивать дорожки так, чтобы данные вывод контактов в коде Грея. To get high angular accuracy, one needs lots of contacts; in order to achieve at least 1 degree accuracy, one needs at least 360 distinct positions per revolution, which requires a minimum of 9 bits of data, and thus the same number of contacts.
If all contacts are placed at the same angular position, then 9 tracks are needed to get a standard BRGC with at least 1 degree accuracy. However, if the manufacturer moves a contact to a different angular position (but at the same distance from the center shaft), then the corresponding "ring pattern" needs to be rotated the same angle to give the same output. If the most significant bit (the inner ring in Figure 1) is rotated enough, it exactly matches the next ring out. Since both rings are then identical, the inner ring can be cut out, and the sensor for that ring moved to the remaining, identical ring (but offset at that angle from the other sensor on that ring). Those two sensors on a single ring make a quadrature encoder. That reduces the number of tracks for a "1 degree resolution" angular encoder to 8 tracks. Reducing the number of tracks still further can't be done with BRGC.
For many years, Torsten Sillke[53] and other mathematicians believed that it was impossible to encode position on a single track such that consecutive positions differed at only a single sensor, except for the 2-sensor, 1-track quadrature encoder. So for applications where 8 tracks were too bulky, people used single-track incremental encoders (quadrature encoders) or 2-track "quadrature encoder + reference notch" encoders.
Norman B. Spedding, however, registered a patent in 1994 with several examples showing that it was possible.[48] Although it is not possible to distinguish 2п positions with п sensors on a single track, it является possible to distinguish close to that many. Etzion and Paterson conjecture that when п is itself a power of 2, п sensors can distinguish at most 2п − 2п positions and that for prime п the limit is 2п − 2 positions.[54] The authors went on to generate a 504 position single track code of length 9 which they believe is optimal. Since this number is larger than 28 = 256, more than 8 sensors are required by any code, although a BRGC could distinguish 512 positions with 9 sensors.
An STGC for п = 30 and п = 5 is reproduced here:
| Angle | Код | Angle | Код | Angle | Код | Angle | Код | Angle | Код | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0° | 10000 | 72° | 01000 | 144° | 00100 | 216° | 00010 | 288° | 00001 | ||||
| 12° | 10100 | 84° | 01010 | 156° | 00101 | 228° | 10010 | 300° | 01001 | ||||
| 24° | 11100 | 96° | 01110 | 168° | 00111 | 240° | 10011 | 312° | 11001 | ||||
| 36° | 11110 | 108° | 01111 | 180° | 10111 | 252° | 11011 | 324° | 11101 | ||||
| 48° | 11010 | 120° | 01101 | 192° | 10110 | 264° | 01011 | 336° | 10101 | ||||
| 60° | 11000 | 132° | 01100 | 204° | 00110 | 276° | 00011 | 348° | 10001 |
Each column is a cyclic shift of the first column, and from any row to the next row only one bit changes.[55]The single-track nature (like a code chain) is useful in the fabrication of these wheels (compared to BRGC), as only one track is needed, thus reducing their cost and size.The Gray code nature is useful (compared to chain codes, также называемый De Bruijn sequences), as only one sensor will change at any one time, so the uncertainty during a transition between two discrete states will only be plus or minus one unit of angular measurement the device is capable of resolving.[56]
Two-dimensional Gray code

Two-dimensional Gray codes are used in communication to minimize the number of bit errors in quadrature amplitude modulation adjacent points in the созвездие. In a typical encoding the horizontal and vertical adjacent constellation points differ by a single bit, and diagonal adjacent points differ by 2 bits.[57]
Gray isometry
The bijective mapping { 0 ↔ 00, 1 ↔ 01, 2 ↔ 11, 3 ↔ 10 } establishes an isometry между metric space над finite field with the metric given by the Hamming distance and the metric space over the finite ring (the usual modular arithmetic) with the metric given by the Lee distance. The mapping is suitably extended to an isometry of the Hamming spaces и . Its importance lies in establishing a correspondence between various "good" but not necessarily linear codes as Gray-map images in из ring-linear codes из .[58][59]
Related codes
There are a number of binary codes similar to Gray codes, including:
- Datex codes aka Giannini codes (1954), as described by Carl P. Spaulding,[17][60][61][62][63][16] use a variant of O'Brien code II.
- Codes used by Varec (ca. 1954),[64][65][66][67] use a variant of O'Brien code I as well as base-12 and base-16 Gray code variants.
- Lucal code (1959)[1][2][35] aka modified reflected binary code (MRB)[1][2]
- Gillham code (1961/1962),[61][68][16][69][70] uses a variant of Datex code and O'Brien code II.
- Leslie and Russell code (1964)[71][18][72][68]
- Royal Radar Establishment code[68]
- Hoklas code (1988)[73][74][75]
Следующее binary-coded decimal (BCD) codes are Gray code variants as well:
- Petherick code (1953),[7][76][77][78][74][nb 3] также известный как Royal Aircraft Establishment (RAE) code.[79]
- O'Brien codes I and II (1955)[80][81][82][62][63][74] (An O'Brien type-I code[nb 4] was already described by Frederic A. Foss of IBM[83][84] and used by Varec in 1954. Later, it was also known as Watts code or Watts reflected decimal (WRD) code.[85][9][10][86][87][88][89][90][nb 1] An O'Brien type-II code was already used by Datex in 1954.[nb 3])
- Excess-3 Gray code (1956)[91] (aka Gray excess-3 code,[62][63][16] Gray 3-excess code, reflex excess-3 code, excess Gray code,[74] Gray excess code, 10-excess-3 Gray code or Gray–Stibitz code), described by Frank P. Turvey Jr. of ITT.[91]
- Tompkins codes I and II (1956)[12][81][82][62][63][74]
- Glixon code (1957)[92][93][94][81][82][62][63][74][nb 4]
| Имя | Кусочек | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Weights | Треки | Compl. | Cyclic | 5 с | Comment |
| серый | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0..3 | 4 | - | (2, 4, 8, 16) | - | [81][82] |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |||||||
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | |||||||
| Павел | 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1..3 | 4 | - | 2, 10 | - | [95] |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |||||||
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | |||||||
| Glixon | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0..3 | 4 | - | 2, 4, 8, 10 | shifted +1 | [92][81][82][93][94][nb 4] |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |||||||
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | |||||||
| Tompkins I | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0..4 | 2 | - | 2, 4, 10 | + | [12][81][82] |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | |||||||
| O'Brien I (Watts) | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0..3 | 4 | 9[nb 5] | 2, 4, 10 | + | [80][81][82][nb 4] |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |||||||
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | |||||||
| Petherick (RAE) | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1..3 | 3 | 2, 10 | + | [7][78][nb 3] | |
| 3 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |||||||
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |||||||
| O'Brien II | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1..3 | 3 | 9[nb 5] | 2, 10 | + | [80][81][82][nb 3] |
| 3 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||
| 2 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | |||||||
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |||||||
| Susskind | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1..4 | 3 | 2, 10 | + | [14] | |
| 3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |||||||
| 2 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | |||||||
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |||||||
| Klar | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0..4 | 4 | 2, 10 | + | [96][97] | |
| 3 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |||||||
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | |||||||
| Tompkins II | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1..3 | 2 | 9[nb 6] | 2, 10 | + | [12][81][82] |
| 3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||
| 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |||||||
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | |||||||
| Excess-3 Gray | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1..4 | 4 | - | 2, 10 | + | [16][74] |
| 3 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |||||||
| 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |||||||
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | |||||||
Смотрите также
- Linear feedback shift register
- De Bruijn sequence - a Gray code on a larger alphabet than {0,1}.
- Steinhaus–Johnson–Trotter algorithm, an algorithm that generates Gray codes for the factorial number system
- Minimum distance code
Примечания
- ^ а б c By applying a simple inversion rule, the Gray code and the O'Brien code I can be translated into the 8421 pure binary code and the 2421 Aiken code, respectively, to ease arithmetic operations.[A]
- ^ Sequence 0, 1, 0, 2, 0, 1, 0, 3, … (sequence A007814 в OEIS).
- ^ а б c d By interchanging and inverting three bit columns, the O'Brien code II и Petherick code can be transferred into each other.
- ^ а б c d By swapping two pairs of bit columns, individually shifting four bit columns and inverting one of them, the Glixon code и O'Brien code I can be transferred into each other.
- ^ а б За O'Brien codes I и II, а 9s complement can be derived by inverting the most-significant (fourth) binary digit.
- ^ За Tompkins code II, а 9s complement can be derived by inverting the first three digits and swapping the two middle binary digits.
Рекомендации
- ^ а б c Lucal, Harold M. (December 1959). "Arithmetic Operations for Digital Computers Using a Modified Reflected Binary". IRE Transactions on Electronic Computers. EC-8 (4): 449–458. Дои:10.1109/TEC.1959.5222057. ISSN 0367-9950. S2CID 206673385. (10 pages)
- ^ а б c Sellers, Jr., Frederick F.; Hsiao, Mu-Yue; Bearnson, Leroy W. (November 1968). Error Detecting Logic for Digital Computers (1-е изд.). Нью-Йорк, США: McGraw-Hill Book Company. pp. 152–164. LCCN 68-16491. OCLC 439460.
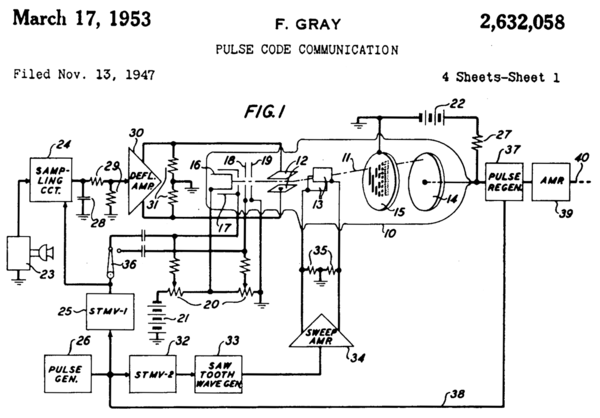
- ^ Gray, Frank (1953-03-17) [1947-11-13]. Pulse Code Communication (PDF). Нью-Йорк, США: Bell Telephone Laboratories, Incorporated. U.S. Patent 2,632,058 . Serial No. 785697. В архиве (PDF) from the original on 2020-08-05. Получено 2020-08-05. (13 pages)
- ^ Breckman, Jack (1956-01-31) [1953-12-31]. Encoding Circuit (PDF). Long Branch, New Jersey, USA: US Secretary of the Army. U.S. Patent 2,733,432 . Serial No. 401738. В архиве (PDF) from the original on 2020-08-05. Получено 2020-08-05. (8 pages)
- ^ а б Ragland, Earl Albert; Schultheis, Jr., Harry B. (1958-02-11) [1953-10-16]. Direction-Sensitive Binary Code Position Control System (PDF). North Hollywood, California, USA: Bendix Aviation Corporation. U.S. Patent 2,823,345 . Serial No. 386524. В архиве (PDF) from the original on 2020-08-05. Получено 2020-08-05. (10 pages)
- ^ Domeshek, Sol; Reiner, Stewart (1958-06-24) [1954-01-08]. Automatic Rectification System (PDF). US Secretary of the Navy. U.S. Patent 2,839,974 . Serial No. 403085. В архиве (PDF) from the original on 2020-08-05. Получено 2020-08-05. (8 pages)
- ^ а б c Petherick, Edward John (October 1953). A Cyclic Progressive Binary-coded-decimal System of Representing Numbers (Technical Note MS15). Farnborough, UK: Royal Aircraft Establishment (RAE). (4 pages) (NB. Sometimes referred to as A Cyclic-Coded Binary-Coded-Decimal System of Representing Numbers.)
- ^ а б Winder, C. Farrell (October 1959). "Shaft Angle Encoders Afford High Accuracy" (PDF). Electronic Industries. Chilton Company. 18 (10): 76–80. Получено 2018-01-14.
[…] The type of code wheel most popular in optical encoders contains a cyclic binary code pattern designed to give a cyclic sequence of "on-off" outputs. The cyclic binary code is also known as the cyclic progression code, the reflected binary code, and the Gray code. This code was originated by G. R. Stibitz, из Bell Telephone Laboratories, and was first proposed for pulse code modulation systems by Frank Gray, also of BTL. Thus the name Gray code. It is also named as "Unit Distance Code" as any two adjacent codes is differ by one (1). The Gray or cyclic code is used mainly to eliminate the possibility of errors at code transition which could result in gross ambiguities. […]
- ^ а б Evans, David Silvester (1960). Fundamentals of Digital Instrumentation (1-е изд.). London, UK: Hilger & Watts Ltd. Получено 2020-05-24. (39 pages)
- ^ а б Evans, David Silvester (March 1961). "Chapter Three: Direct Reading from Coded Scales". Digital Data: Their derivation and reduction for analysis and process control (1-е изд.). London, UK: Hilger & Watts Ltd / Interscience Publishers. pp. 18–23. Получено 2020-05-24. п. 20–23:
[…] Decoding. […] To decode C.P.B or W.R.D. codes, a simple inversion rule can be applied. The readings of the higher tracks determine the way in which the lower tracks are translated. The inversion rule is applied line by line for the C.P.B. and for the W.R.D it is applied decade by decade or line by line. Starting therefore with the top or slowest changing track of the C.P.B., if the result is odd (1) the next track value has to be inverted, i.e. 0 for 1 and 1 for 0. If, however, the first track is even (0), the second track is left as read, i.e. 0 for 0 and 1 for 1. Again, if the resultant reading of the second track is odd, the third track reading is inverted and so on. When an odd is changed to an even the line below is not inverted and when an even is changed to an odd the line below is inverted. The result of applying this rule to the pattern […] is the pure binary (P.B.) pattern […] where each track or digit can be given a definite numerical value (in this instance 1, 2, 4, 8, etc.). […] Using the line-by-line inversion rule on the W.R.D. code produces [a] pattern [of 1, 2, 4, 2 code] where again the digits can be given numerical values and summed decade by decade. The summing of the digits can be very useful, for example, in a high-speed scanning system; but in a parallel decoding system […], it is usual to treat each binary quartet or decade as an entity. In other words, if the first or more significant decade is odd, the second decade is rectified or complemented by inverting the D track and so on, the result being the repeating pattern of [rectified W.R.D. code]. This is an extremely easy thing to achieve since the only change required is the inversion of the meaning of the D track or complementing digit. […]
(8+82 pages) (NB. The author does not mention Gray at all and calls the standard Gray code "Cyclic Permuted Binary Code" (C.P.B.), the book index erroneously lists it as "cyclic pure binary code".) - ^ Newson, P. A. (1965). Tables for the Binary Encoding of Angles (1-е изд.). United Kingdom Atomic Energy Authority, Research Group, Научно-исследовательский центр по атомной энергии, Harwell, UK: H. M. Stationery Office. Получено 2020-05-24. (12 pages)
- ^ а б c d Tompkins, Howard E. (September 1956) [1956-07-16]. "Unit-Distance Binary-Decimal Codes for Two-Track Commutation". IRE Transactions on Electronic Computers. Correspondence. Moore School of Electrical Engineering, Пенсильванский университет, Philadelphia, Pennsylvania, USA. EC-5 (3): 139. Дои:10.1109/TEC.1956.5219934. ISSN 0367-9950. Получено 2020-05-18. (1 page)
- ^ а б Kautz, William H. (June 1958). "Unit-Distance Error-Checking Codes". IRE Transactions on Electronic Computers. EC-7 (2): 179–180. Дои:10.1109/TEC.1958.5222529. ISSN 0367-9950. S2CID 26649532. (2 pages)
- ^ а б Susskind, Alfred Kriss; Ward, John Erwin (1958-03-28) [1957, 1956]. "III.F. Unit-Distance Codes / VI.E.2. Reflected Binary Codes". Written at Cambridge, Massachusetts, USA. In Susskind, Alfred Kriss (ed.). Notes on Analog-Digital Conversion Techniques. Technology Books in Science and Engineering. 1 (3 ed.). Нью-Йорк, США: Technology Press of the Massachusetts Institute of Technology / John Wiley & Sons, Inc. / Chapman & Hall, Ltd. pp. 3-10–3-16 [3-13–3-16], 6-65–6-60 [6-60]. (x+416+2 pages) (NB. The contents of the book was originally prepared by staff members of the Servomechanisms Laboraratory, Department of Electrical Engineering, Массачусетский технологический институт, for Special Summer Programs held in 1956 and 1957. Susskind's "reading-type code" is actually a minor variant of the code shown here with the two most significant bit columns swapped to better illustrate symmetries. Also, by swapping two bit columns and inverting one of them, the code can be transferred into the Petherick code, whereas by swapping and inverting two bit columns, the code can be transferred into the O'Brien code II.)
- ^ а б Chinal, Jean P. (January 1973). "3.3. Unit Distance Codes". Written at Paris, France. Design Methods for Digital Systems. Translated by Preston, Alan; Summer, Arthur (1st English ed.). Berlin, Germany: Akademie-Verlag / Springer-Verlag. п. 50. Дои:10.1007/978-3-642-86187-1_3. ISBN 978-0-387-05871-9. License No. 202-100/542/73. Order No. 7617470(6047) ES 19 B 1 / 20 K 3. Получено 2020-06-21. (xviii+506 pages) (NB. The French 1967 original book was named "Techniques Booléennes et Calculateurs Arithmétiques", published by Éditions Dunod.)
- ^ а б c d е ж Military Handbook: Encoders – Shaft Angle To Digital (PDF). United States Department of Defense. 1991-09-30. MIL-HDBK-231A. В архиве (PDF) from the original on 2020-07-25. Получено 2020-07-25. (NB. Supersedes MIL-HDBK-231(AS) (1970-07-01).)
- ^ а б c Spaulding, Carl P. (1965-01-12) [1954-03-09]. "Digital coding and translating system" (PDF). Monrovia, California, USA: Datex Corporation. U.S. Patent 3165731A . Serial No. 415058. В архиве (PDF) from the original on 2020-08-05. Получено 2018-01-21. (28 pages)
- ^ а б Russell, A. (August 1964). "Some Binary Codes and a Novel Five-Channel Code". Control (Systems, Instrumentation, Data Processing, Automation, Management, incorporating Automation Progress). Special Features. London, UK: Morgan-Grampain (Publishers) Limited. 8 (74): 399–404. Получено 2020-06-22. (6 pages)
- ^ Pickover, Clifford A. (2009). The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics. Sterling Publishing Company. п. 392. ISBN 978-1-40275796-9.
- ^ а б c d Knuth, Donald Ervin (2004-10-15). "Generating all п-tuples". The Art of Computer Programming, Volume 4A: Enumeration and Backtracking. pre-fascicle 2a.
- ^ Heath, F. G. (September 1961). "Pioneers Of Binary Coding". Journal of the Institution of Electrical Engineers. Manchester College of Science and Technology, Faculty of Technology of the Манчестерский университет, Manchester, UK: Институт инженерии и технологий (IET). 7 (81): 539–541. Дои:10.1049/jiee-3.1961.0300. Получено 2020-06-22. (3 pages)
- ^ Cattermole, Kenneth W. (1969). Written at Harlow, Essex, UK. Principles of pulse code modulation (1-е изд.). London, UK / New York, USA: Iliffe Books Ltd. / American Elsevier Publishing Company, Inc. pp. 245, 434. ISBN 978-0-444-19747-4. LCCN 78-80432. SBN 444-19747-8. п. 245:
[…] There seems to be some confusion about the attributation of this code, because two inventors named Gray have been associated with it. When I first heard the name I took it as referring to Elisha Gray, и Хит testifies to his usage of it. Many people take it as referring to Frank Gray из Bell Telephone Laboratories, who in 1947 first proposed its use in coding tubes: his patent is listed in the bibliography. […]
(2+448+2 pages) - ^ Edwards, Anthony William Fairbank (2004). Cogwheels of the Mind: The Story of Venn Diagrams. Baltimore, Maryland, USA: Johns Hopkins University Press. pp. 48, 50. ISBN 0-8018-7434-3. ISBN 978-0-8018-7434-5.
- ^ Goodall, William M. (January 1951). "Television by Pulse Code Modulation". Bell System Technical Journal. 30 (1): 33–49. Дои:10.1002/j.1538-7305.1951.tb01365.x. (NB. Presented orally before the I.R.E. National Convention, New York City, March 1949.)
- ^ Wakerly, John F. (1994). Digital Design: Principles & Practices. Нью-Джерси, США: Prentice Hall. pp. 48–49, 222. ISBN 0-13-211459-3. ISBN 978-0-13-211459-2. (NB. The two page sections taken together say that K-maps are labeled with Gray code. The first section says that they are labeled with a code that changes only one bit between entries and the second section says that such a code is called Gray code.)
- ^ Brown, Frank Markham (2012) [2003, 1990]. Boolean Reasoning – The Logic of Boolean Equations (reissue of 2nd ed.). Mineola, New York: Dover Publications, Inc. п. 49. ISBN 978-0-486-42785-0. 1st edition
- ^ Händler, Wolfgang (1958). Ein Minimisierungsverfahren zur Synthese von Schaltkreisen (Minimisierungsgraphen) (Dissertation) (in German). Potsdam, Germany: Technische Hochschule Darmstadt. D 17. (73 pages+app.) [1]
- ^ Berger, Erich R.; Händler, Wolfgang (1967) [1962]. Steinbuch, Karl W.; Wagner, Siegfried W. (eds.). Taschenbuch der Nachrichtenverarbeitung (in German) (2 ed.). Berlin, Germany: Springer-Verlag OHG. pp. 64, 1034–1035, 1036, 1038. LCCN 67-21079. Title No. 1036. p. 64:
[…] Übersichtlich ist die Darstellung nach Händler, die sämtliche Punkte, numeriert nach dem Gray-Code […], auf dem Umfeld eines Kreises anordnet. Sie erfordert allerdings sehr viel Platz. […]
[Händler's diagram, where all points, numbered according to the Gray code, are arranged on the circumference of a circle, is easily comprehensible. It needs, however, a lot of space.] - ^ "Informatik Sammlung Erlangen (ISER)" (на немецком). Erlangen, Germany: Friedrich-Alexander Universität. 2012-03-13. Архивировано из оригинал on 2017-05-16. Получено 2017-04-12.
- ^ "Informatik Sammlung Erlangen (ISER) – Impressum" (на немецком). Erlangen, Germany: Friedrich-Alexander Universität. 2012-03-13. В архиве from the original on 2012-02-26. Получено 2017-04-15.
- ^ а б c d е Bhat, Girish S.; Savage, Carla Diane (1996). "Balanced Gray Codes". Electronic Journal of Combinatorics. 3 (1). Дои:10.37236/1249.
- ^ Donohue, Ryan (2003). "Synchronization in Digital Logic Circuits" (PDF). В архиве (PDF) from the original on 2018-01-15. Получено 2018-01-15.
- ^ Hulst, George D. (1962-02-06) [1957-11-15]. Reflected binary code counter (PDF). Nutley, New Jersey, USA: International Telephone and Telegraph Corporation (ITT). U.S. Patent 3,020,481 . Serial No. 696793. В архиве (PDF) from the original on 2020-08-06. Получено 2020-08-06. (5 pages)
- ^ Mehta, Huzefa; Owens, Robert Michael; Irwin, Mary Jane "Janie" (1996-03-22). Some issues in Gray code addressing. Proceedings of the 6th Great Lakes Symposium on VLSI (GLSVLSI 96). IEEE Computer Society. pp. 178–181. Дои:10.1109/GLSV.1996.497616. ISBN 978-0-8186-7502-7. ISSN 1066-1395.
- ^ а б Doran, Robert "Bob" William (March 2007). The Gray Code (PDF). CDMTCS Research Report Series. Centre for Discrete Mathematics and Theoretical Computer Science, University of Auckland, Новая Зеландия. CDMTCS-304. В архиве (PDF) from the original on 2020-05-22. Получено 2020-05-23. (25 pages)
- ^ Su, Ching-Long; Tsui, Chi-Ying; Despain, Alvin M. (1994). Low Power Architecture Design and Compilation Techniques for High-Performance Processors (PDF) (Отчет). Advanced Computer Architecture Laboratory. ACAL-TR-94-01.
- ^ Guo, Hui; Parameswaran, Sri (April–June 2010). "Shifted Gray encoding to reduce instruction memory address bus switching for low-power embedded systems". Journal of Systems Architecture. 56 (4–6): 180–190. Дои:10.1016/j.sysarc.2010.03.003.
- ^ Dietz, Henry Gordon. "The Aggregate Magic Algorithms: Gray Code Conversion".
- ^ а б Guan, Dah-Jyh (1998). "Generalized Gray Codes with Applications". Proceedings of the National Scientific Council, Republic of China, Part A. 22: 841–848. CiteSeerX 10.1.1.119.1344.
- ^ а б Suparta, I. Nengah (2005). "A simple proof for the existence of exponentially balanced Gray codes". Electronic Journal of Combinatorics. 12. Дои:10.37236/1986.
- ^ а б Flahive, Mary Elizabeth; Bose, Bella (2007). "Balancing cyclic р-ary Gray codes". Electronic Journal of Combinatorics. 14. Дои:10.37236/949.
- ^ Strackx, Raoul; Piessens, Frank (2016). "Ariadne: A Minimal Approach to State Continuity". Usenix Security. 25.
- ^ а б Savage, Carla Diane; Winkler, Peter (1995). "Monotone Gray codes and the middle levels problem". Journal of Combinatorial Theory, Series A. 70 (2): 230–248. Дои:10.1016/0097-3165(95)90091-8. ISSN 0097-3165.
- ^ Savage, Carla Diane (1997-01-16). "Long cycles in the middle two levels of the Boolean lattice". Ars Combinatoria. North Carolina State University, Raleigh, North Carolina, USA. 35 (A): 97–108. CiteSeerX 10.1.1.39.2249. ISSN 0381-7032. S2CID 15975960. В архиве from the original on 2020-05-13. Получено 2020-05-13. (15 pages)
- ^ а б Goddyn, Luis (1999). "MATH 343 Applied Discrete Math Supplementary Materials" (PDF). Department of Mathematics, Университет Саймона Фрейзера. Архивировано из оригинал (PDF) on 2015-02-17.
- ^ Sawada, Joseph "Joe"; Wong, Dennis Chi-Him (2007). "A Fast Algorithm to generate Beckett–Gray codes". Electronic Notes in Discrete Mathematics. 29: 571–577. Дои:10.1016/j.endm.2007.07.091.
- ^ Richards, Richard Kohler (January 1971). "Snake-in-the-Box Codes". Written at Ames, Iowa, USA. Digital Design. Нью-Йорк, США: Wiley-Interscience, John Wiley & Sons, Inc. pp. 206–207. ISBN 0-471-71945-5. LCCN 73-147235. (12+577+1 pages)
- ^ а б NZ 264738, Spedding, Norman Bruce, "A position encoder", published 1994-10-28[неудачная проверка]
- ^ Spedding, Norman Bruce (1994-10-28). "The following is a copy of the provisional patent filed on behalf of Industrial Research Limited on 1994-10-28 – NZ Patent 264738" (PDF). Industrial Research Limited. NZ Patent 264738. В архиве (PDF) from the original on 2017-10-29. Получено 2018-01-14.
- ^ Hiltgen, Alain P.; Paterson, Kenneth G.; Brandestini, Marco (September 1996). "Single-Track Gray Codes" (PDF). IEEE Transactions on Information Theory. 42 (5): 1555–1561. Дои:10.1109/18.532900. Zbl 857.94007.
- ^ Hiltgen, Alain P.; Paterson, Kenneth G. (September 2001). "Single-Track Circuit Codes" (PDF). IEEE Transactions on Information Theory. 47 (6): 2587–2595. CiteSeerX 10.1.1.10.8218. Дои:10.1109/18.945274. В архиве (PDF) from the original on 2018-01-15. Получено 2018-01-15.
- ^ Etzion, Tuvi; Schwartz, Moshe (November 1999) [1998-05-17]. "The Structure of Single-Track Gray Codes" (PDF). IEEE Transactions on Information Theory. IT-45 (7): 2383–2396. CiteSeerX 10.1.1.14.8333. Дои:10.1109/18.796379. В архиве (PDF) from the original on 2018-01-15. Получено 2018-01-15. Technical Report CS0937
- ^ Sillke, Torsten (1997) [1993-03-01]. "Gray-Codes with few tracks (a question of Marco Brandestini)". В архиве from the original on 2017-10-29. Получено 2017-10-29.
- ^ Etzion, Tuvi; Paterson, Kenneth G. (May 1996). "Near Optimal Single-Track Gray Codes" (PDF). IEEE Transactions on Information Theory. IT-42 (3): 779–789. CiteSeerX 10.1.1.14.1527. Дои:10.1109/18.490544. В архиве (PDF) from the original on 2016-10-30. Получено 2018-04-08.
- ^ Ruskey, Frank; Weston, Mark (2005-06-18). "A Survey of Venn Diagrams: Symmetric Diagrams". Dynamic Surveys. Electronic Journal of Combinatorics. Дои:10.37236/26.
- ^ Alciatore, David G.; Histand, Michael B. (1999). Mechatronics. McGraw–Hill Education – Europe. ISBN 978-0-07-131444-2.
- ^ Krishna (2008-05-11). "Gray code for QAM". В архиве from the original on 2017-10-29. Получено 2017-10-29.
- ^ Greferath, Marcus (2009). "An Introduction to Ring-Linear Coding Theory". In Sala, Massimiliano; Mora, Teo; Perret, Ludovic; Sakata, Shojiro; Traverso, Carlo (eds.). Gröbner Bases, Coding, and Cryptography. Springer Science & Business Media. п.220. ISBN 978-3-540-93806-4.
- ^ Solé, Patrick (2016-04-17). Hazewinkel, Michiel (ред.). Kerdock and Preparata codes. Энциклопедия математики. Springer Science+Business Media. ISBN 1-4020-0609-8. ISBN 978-1-4020-0609-8. В архиве from the original on 2017-10-29. Получено 2017-10-29.
- ^ Spaulding, Carl P. (1965-07-12). How to Use Shaft Encoders. Monrovia, California, USA: Datex Corporation. (85 pages)
- ^ а б Wheeler, Edwin L. (1969-12-30) [1968-04-05]. Analog to digital encoder (PDF). New York, USA: Conrac Corporation. U.S. Patent 3487460A . Serial No. 719026 (397812). В архиве (PDF) from the original on 2020-08-05. Получено 2018-01-21. п. column 9:
[…] The MOA-GILLHAM code is essentially the combination of the Gray code discussed thereinabove and the well known Datex code; the Datex code is disclosed in U.S. Patent 3,165,731. The arrangement is such that the Datex code defines the bits for the units count of the encoder and the Gray code defines the bits for each of the higher order decades, the tens, hundreds, etc. […]
(11 pages) - ^ а б c d е Dokter, Folkert; Steinhauer, Jürgen (1973-06-18). "2.4. Coding numbers in the binary system". Digital Electronics. Philips Technical Library (PTL) / Macmillan Education (Reprint of 1st English ed.). Eindhoven, Netherlands: The Macmillan Press Ltd. / N. V. Philips' Gloeilampenfabrieken. pp. 32, 39, 50–53. Дои:10.1007/978-1-349-01417-0. ISBN 978-1-349-01419-4. SBN 333-13360-9. Получено 2020-05-11. п. 53:
[…] The Datex code […] uses the O'Brien code II within each decade, and reflected decimal numbers for the decimal transitions. For further processing, code conversion to the natural decimal notation is necessary. Since the O'Brien II code forms a 9s complement, this does not give rise to particular difficulties: whenever the code word for the tens represents an odd number, the code words for the decimal units are given as the 9s complements by inversion of the fourth binary digit. […]
(270 pages) - ^ а б c d е Dokter, Folkert; Steinhauer, Jürgen (1975) [1969]. "2.4.4.6. Einschrittige Kodes". Digitale Elektronik in der Meßtechnik und Datenverarbeitung: Theoretische Grundlagen und Schaltungstechnik. Philips Fachbücher (in German). я (improved and extended 5th ed.). Hamburg, Germany: Deutsche Philips GmbH. pp. 41, 48, 51, 58, 60–61. ISBN 3-87145-272-6. (xii+327+3 pages)
- ^ "…accurate liquid level metering – at ANY DISTANCE!". Petroleum Refiner (Advertisement). Gulf Publishing Company. 33 (9): 368. September 1954. ISSN 0096-6517. п. 368:
[…] The complete dispatching operation, gauging, and remote control is integrated into one single unitized system when a "Varec" Pulse Code Telemetering System is installed. […]
- ^ Bishup, Bernard W.; Repeta, Anthony A.; Giarrizzo, Frank C. (1968-08-13) [1963-04-03]. "Telemetering and supervisory control system having normally continuous telemetering signals". Leeds and Northrup Co. US3397386A. [2]
- ^ "Encoder Pulse Format". Installation and Operations Manual for the Model 1900 Micro 4-Wire Transmitter (PDF). Cypress, California, USA: Whessoe Varec, Inc. January 1993 [1991-07-01]. pp. 04-4–04-8. 33-08461. В архиве (PDF) from the original on 2020-05-16. Получено 2020-05-16. (38 pages) (NB. Position 5 for "Inches" on page 04-8 should read "0111" rather than "1111".)
- ^ "2.2.3.3 MSP Level Data Format". Varec Model 1900 – Micro 4-Wire Transmitter (BSAP to Mark / Space Protocol (MSP)) – Application Notes (PDF). Emerson Electric. pp. 11–14. В архиве (PDF) from the original on 2020-05-16. Получено 2020-05-16. (vi+33 pages)
- ^ а б c Wightman, Eric Jeffrey (1972). "Chapter 6. Displacement measurement". Instrumentation in Process Control (1-е изд.). London, UK: Butterworth & Co (Publishers) Ltd. pp. 122–123. ISBN 0-408-70293-1. ISBN 1-48316335-0, 978-1-48316335-2. п. 122–123:
[…] Other forms of code are also well known. Among these are the Royal Radar Establishment code; В Excess Three decimal code; Gillham code which is recommended by ИКАО for automatic height transmission for управления воздушным движением purposes; то Petherick code, а Leslie and Russell code из National Engineering Laboratory. Each has its particular merits and they are offered as options by various encoder manufacturers. […]
(12+367+5 pages) - ^ Phillips, Darryl (2012-07-26) [1998]. "Altitude – MODEC ASCII". AirSport Avionics. Архивировано из оригинал on 2012-07-26.
- ^ Stewart, K. (2010-12-03). "Aviation Gray Code: Gillham Code Explained". Custom Computer Services (CCS). В архиве from the original on 2018-01-16. Получено 2018-01-14.
- ^ Leslie, William "Bill" H. P.; Russell, A. (1964). A cyclic progressive decimal code for simple translation to decimal and analogue outputs (Отчет). East Kilbride, Glasgow, UK: National Engineering Laboratory. NEL Report 129. (17 pages)
- ^ Leslie, William "Bill" H. P. (1974). "The work on NC at NEL". В Koenigsberger, Franz; Tobias, Stephen Albert (eds.). Proceedings of the Fourteenth International Machine Tool Design and Research Conference, 12–14 September 1973. The Macmillan Press Ltd. pp. 215–224 [215, 217]. ISBN 978-1-34901921-2. LCCN 73-16545. SBN 333-14913-0. ISBN 1-34901921-6.
- ^ Hoklas, Archibald (1989-09-06) [1988-04-29]. "Abtastvorrichtung zur digitalen Weg- oder Winkelmessung" (PDF) (на немецком). VEB Schiffselektronik Johannes Warnke. GDR Patent DD271603A1. WP H 03 M / 315 194 8. Archived from оригинал (PDF) on 2018-01-18. Получено 2018-01-18 - через DEPATIS. [3] [4]
- ^ а б c d е ж грамм Hoklas, Archibald (2005). "Gray code – Unit distance code". В архиве from the original on 2018-01-15. Получено 2018-01-15.
- ^ Hoklas, Archibald (2005). "Gray-Kode – Einschrittiger Abtastkode" (на немецком). В архиве from the original on 2018-01-15. Получено 2018-01-15.
- ^ Petherick, Edward John; Hopkins, A. J. (1958). Некоторые недавно разработанные цифровые устройства для кодирования вращения валов (Техническая нота MS21). Фарнборо, Великобритания: Royal Aircraft Establishment (РАЭ).
- ^ "Дигитайзер как Analog-Digital-Wandler in der Steuer-, Meß- und Regeltechnik" (PDF). Technische Mitteilungen. Relais, elektronische Geräte, Steuerungen (на немецком языке). № 13. Кельн-Ниль, Германия: Франц Баумгартнер (FraBa). Май 1963. С. 1–2. Архивировано из оригинал (PDF) на 2020-05-21. Получено 2020-05-21. стр. 1–2:
[…] Die Firma Harrison Reproduction Equipment, Фарнборо / Англия […] шляпа в jahrelanger Entwicklung в Zusammenarbeit mit der Britischen Luftwaffe und britischen Industriebetrieben den Mechanischen Digitizer […] zu einer technischen Reife gebracht, die fast allen… Genderügen. […] Um bei der dezimalen Entschlüsselung des verwendeten Binärcodes zu eindeutigen und bei der Übergabe von einer Dezimalstelle zur anderen in der Reihenfolge immer Richtigen Ergebnissen zu au kommenliez, wurde eebnissen zu kommenliez, wurde eeglüssen zu kommenlee, seeller seinen Aufbau eine relativ einfache Entschlüsselung erlaubt. Der Code basiert auf dem Код Петерика. […]
(4 страницы) - ^ а б Charnley, C.J .; Bidgood, R.E .; Бордман, Г. Э. Т. (октябрь 1965 г.). «Конструкция пневматического датчика положения» (PDF). Объемы разбирательств МФБ. Колледж воздухоплавания, Крэнфилд, Бедфорд, Англия. 2 (3): 75–88. Дои:10.1016 / S1474-6670 (17) 68955-9. Глава 1.5. Получено 2018-01-14.
- ^ Холлингдейл, Стюарт Х. (1958-09-19). «Сессия 14. Обработка данных». Приложения компьютеров. Атлас - применение компьютеров, Ноттингемский университет, 15–19 сентября 1958 г. (Документ конференции). В архиве из оригинала на 2020-05-25. Получено 2020-05-25.
- ^ а б c О'Брайен, Джозеф А. (май 1956 г.) [1955-11-15, 1955-06-23]. «Циклические десятичные коды для аналого-цифровых преобразователей». Труды Американского института инженеров-электриков, часть I: Связь и электроника. Bell Telephone Laboratories, Уиппани, Нью-Джерси, США. 75 (2): 120–122. Дои:10.1109 / TCE.1956.6372498. ISSN 0097-2452. S2CID 51657314. Документ 56-21. Получено 2020-05-18. (3 страницы) (Примечание. Этот документ был подготовлен для презентации на Зимнем общем собрании AIEE, Нью-Йорк, США, с 30 января 1956 по 03 февраля 1956).
- ^ а б c d е ж грамм час я Штайнбух, Карл В., изд. (1962). Написано в Карлсруэ, Германия. Taschenbuch der Nachrichtenverarbeitung (на немецком языке) (1-е изд.). Берлин / Геттинген / Нью-Йорк: Springer-Verlag OHG. С. 71–74, 97, 761–764, 770, 1080–1081. LCCN 62-14511.
- ^ а б c d е ж грамм час я Штайнбух, Карл В.; Вебер, Вольфганг; Heinemann, Traute, eds. (1974) [1967]. Taschenbuch der Informatik - Band II - Struktur und Programmierung von EDV-Systemen. Taschenbuch der Nachrichtenverarbeitung (на немецком). 2 (3-е изд.). Берлин, Германия: Springer Verlag. С. 98–100. ISBN 3-540-06241-6. LCCN 73-80607. ISBN 978-3-540-06241-7.
- ^ Фосс, Фредерик А. (1960-12-27) [1954-12-17]. "Системы управления" (PDF). International Business Machines Corp.. Рис.7, Рис.8, Рис.11. Патент США 2966670A . Серийный номер 475945. В архиве (PDF) из оригинала на 21.06.2020. Получено 2020-08-05. (14 страниц) (NB. Автор назвал свой код 2 * -4-2-1 (+ 9- ± 7- ± 3- ± 1) отраженным десятичным кодом.)
- ^ Фосс, Фредерик А. (декабрь 1954 г.). «Использование отраженного кода в цифровых системах управления». Операции IRE на электронных компьютерах. ИС-3 (4): 1–6. Дои:10.1109 / IREPGELC.1954.6499244. ISSN 2168-1740. (6 страниц)
- ^ Эванс, Дэвид Сильвестр (1958). "[неизвестный]". Сделки. Институт Измерения и Контроля. 10–12: 87. Cite использует общий заголовок (помощь) (NB. Код Уоттса был назван кодом W.R.D. или отраженным десятичным числом Уоттса, чтобы отличать его от других кодов, используемых в Hilger & Watts Ltd..)
- ^ Benjamin, P.W .; Николлс, Г. С. (1963). «3.2.2 Электромеханические дигитайзеры». Измерение нейтронных спектров с помощью полуавтоматического сканирования протонов отдачи в фотоэмульсиях. Управление по атомной энергии Соединенного Королевства, Центр исследования атомного оружия, ВЕЛИКОБРИТАНИЯ: Министерство энергетики США. С. 8–10, 19. Отчет AWRE № NR 5/63. [5] (23 страницы)
- ^ Клинковски, Джеймс Дж. (14 марта 1967 г.) [23 марта 1964 г.]. "Электронные схемы диодно-матричного декодера" (PDF). Детройт, Мичиган, США: Корпорация Берроуз. Патент США 3309695A . Серийный номер 353845. В архиве (PDF) из оригинала 2020-05-23. Получено 2020-05-23. (5 страниц) [6]
- ^ Клинковски, Джеймс Дж. (31 марта 1970 г.) [22 декабря 1966 г.]. «Преобразователь двоично-десятичных сигналов» (PDF). Детройт, Мичиган, США: Корпорация Берроуз. Патент США 3504363A . Серийный номер 603926. В архиве (PDF) из оригинала 2020-05-23. Получено 2020-05-23. (7 страниц)
- ^ "[неизвестный]". Новости электрического дизайна. Издательство Роджерс. 12. 1967. ISSN 0012-7515. Cite использует общий заголовок (помощь) [7][8]
- ^ Тот-Зентаи, Дьёрдьи (1979-10-05). «Некоторые проблемы угловых вращательных цифровых преобразователей». Периодика Политехника Электротехника. Кафедра электронных технологий, Технический университет, Будапешт, Венгрия. 23 (3–4): 265–270 [266]. Получено 2020-05-23. (NB. Показывает 6-значный код мощности.)
- ^ а б Терви младший, Фрэнк П. (1958-07-29) [1956-05-17]. «Кодер счетчика импульсов» (PDF). Натли, Нью-Джерси, США: Международная телефонная и телеграфная корпорация. Патент США 2845617A. . Серийный номер 585494. В архиве (PDF) из оригинала 2020-05-23. Получено 2020-05-23. (5 страниц)
- ^ а б Гликсон, Гарри Роберт (март 1957). «Можете ли вы воспользоваться преимуществами циклического двоично-десятичного кода?». Инженерия управления (CtE). Техническое Издательство. 4 (3): 87–91. ISSN 0010-8049. (5 страниц)
- ^ а б Боруки, Лоренц; Диттманн, Иоахим (1971) [июль 1970, 1966, осень 1965]. «2.3 Gebräuchliche Codes in der digitalen Meßtechnik». Написано в Крефельде / Карлсруэ, Германия. Digitale Meßtechnik: Eine Einführung (на немецком языке) (2-е изд.). Берлин / Гейдельберг, Германия: Springer-Verlag. С. 10–23 [12–14]. Дои:10.1007/978-3-642-80560-8. ISBN 3-540-05058-2. LCCN 75-131547. ISBN 978-3-642-80561-5. (viii + 252 стр.) 1-е издание (NB. Нравится Каммерер, авторы описывают 6-битный 20-циклический код Glixon.)
- ^ а б Каммерер, Вильгельм (Май 1969 г.). «II.15. Informationsdarstellung im Automaten». Написано в Йене, Германия. В Фрюхауф, Ганс; Каммерер, Вильгельм; Шредер, Курц; Винклер, Гельмут (ред.). Digitale Automaten - Theorie, Struktur, Technik, Programmieren. Elektronisches Rechnen und Regeln (на немецком языке). 5 (1-е изд.). Берлин, Германия: Akademie-Verlag GmbH. п. 173. Лицензия №. 202-100 / 416/69. № заказа. 4666 ES 20 К 3. (NB. Существует также второе издание 1973 года. Боруки и Диттманн, но не называя его кодом Glixon, автор создает 20-циклический тетрадный код из кода Glixon и вариант кода Glixon с инвертированным старшим битом.)
- ^ Пол, Маттиас Р. (1995-08-10) [1994]. "Unterbrechungsfreier Schleifencode" [Код непрерывного цикла]. 1.02 (на немецком языке). Получено 2008-02-11. (NB. Автор назвал этот код Schleifencode (Английский: «код цикла»). Он отличается от BCD-кода Грея только кодированием состояния 0, чтобы сделать его циклическим кодом единичного расстояния для приложений полного вращения. Избегание шаблона кода с нулями позволяет проводить самотестирование контура и использовать линии данных для бесперебойного распределения энергии.)
- ^ Клар, Райнер (1970-02-01). Digitale Rechenautomaten - Eine Einführung [Цифровые компьютеры - Введение]. Sammlung Göschen (на немецком языке). 1241 / 1241a (1-е изд.). Берлин, Германия: Walter de Gruyter & Co. / G. J. Göschen'sche Verlagsbuchhandlung. п. 17. ISBN 3-11-083160-0. ISBN 978-3-11-083160-3. Archiv-Nr. 7990709. В архиве из оригинала на 2020-06-01. Получено 2020-04-13. (205 страниц) (NB. Переиздание первого издания 2019 г. доступно по ссылке ISBN 3-11002793-3, 978-3-11002793-8. Переработанный и расширенный 4-е издание тоже существует.)
- ^ Клар, Райнер (1989) [1988-10-01]. Digitale Rechenautomaten - Eine Einführung in die Struktur von Computerhardware [Цифровые компьютеры - Введение в структуру компьютерного оборудования]. Sammlung Göschen (на немецком языке). 2050 (4-е переработанное изд.). Берлин, Германия: Walter de Gruyter & Co. п. 28. ISBN 3-11011700-2. ISBN 978-3-11011700-4. (320 страниц) (NB. Автор назвал этот код Einheitsabstandscode (Английский: «код расстояния»). Поменяв местами два битовых столбца и инвертируя один из них, его можно перенести в Код О'Брайена II, тогда как путем перестановки и инвертирования двух битовых столбцов его можно перенести в Код Петерика.)
дальнейшее чтение
- Ричардс, Ричард Колер (1955). Арифметические операции в цифровых компьютерах (5-е изд.). Нью-Йорк, США: D. Van Nostrand Co., Inc.
- Ричардс, Ричард Колер (1967). Электронные цифровые компоненты и схемы. D. Van Nostrand Co., Inc. С. 490, 500–504, 510–511.
- Блэк, Пол Э. (25 февраля 2004 г.). «Код Грея». NIST.
- Press, William H .; Teukolsky, Saul A .; Веттерлинг, Уильям Т .; Фланнери, Брайан П. (2007). «Раздел 22.3. Коды Грея». Числовые рецепты: искусство научных вычислений (3-е изд.). Нью-Йорк, США: Издательство Кембриджского университета. ISBN 978-0-521-88068-8.
- Дикарь, Карла Дайан (1997). "Обзор комбинаторных кодов Грея". SIAM Обзор. Общество промышленной и прикладной математики (СИАМ). 39 (4): 605–629. CiteSeerX 10.1.1.39.1924. Дои:10.1137 / S0036144595295272. JSTOR 2132693.
- Уилф, Герберт Сол (1989). «Главы 1–3». Комбинаторные алгоритмы: обновление. Общество промышленной и прикладной математики (СИАМ). ISBN 0-89871-231-9. ISBN 978-0-89871-231-5.
- Дьюар, Меган; Стивенс, Бретт (29 августа 2012 г.). Заказ блочных конструкций - коды Грея, универсальные циклы и конфигурация. CMS Книги по математике (1-е изд.). Нью-Йорк, США: Springer Science + Business Media. Дои:10.1007/978-1-4614-4325-4. ISBN 978-1-46144324-7. ISSN 1613-5237. ISBN 1-46144324-5.
- Максфилд, Клайв «Макс» (01.10.2012) [28.05.2011]. "Основы кода Грея". Как сделать дизайн. EETimes. Часть 1. В архиве с оригинала на 30.10.2017. Получено 2017-10-30. Часть 2 Часть 3
- Уоррен-младший, Генри С. (2013). «Глава 13: Код Грея». Хакерское наслаждение (2-е изд.). Эддисон Уэсли – Pearson Education, Inc. С. 311–317. ISBN 978-0-321-84268-8. (7 страниц)
- Зиновик, Игорь; Кронинг, Даниэль; Чебиряк, Юрий (21.03.2008). «Вычисление двоичных комбинаторных кодов Грея с помощью исчерпывающего поиска с помощью SAT-решателей». IEEE Transactions по теории информации. IEEE. 54 (4): 1819–1823. Дои:10.1109 / TIT.2008.917695. HDL:20.500.11850/11304. (5 страниц)
- О'Брайен, Джозеф А. (июнь 1957 г.). "Преобразователи двоично-десятичного кода единиц измерения расстояния". Операции IRE на электронных компьютерах. ИС-6 (2): 122–123. Дои:10.1109 / TEC.1957.5221585. ISSN 0367-9950. Получено 2020-05-25. (2 страницы)
- Барр, К. Г. (март 1981). «Десятичный код Грея - легко конвертируется для кодирования положения вала» (PDF). Беспроводной мир. Vol. 87 нет. 1542. Факультет естественных наук, Университет Вест-Индии. С. 86–87. В архиве (PDF) из оригинала на 2020-07-28. Получено 2020-07-28.
внешняя ссылка
- Демонстрация "кода серого" Майкл Шрайбер, Вольфрам Демонстрационный проект (с реализацией Mathematica). 2007 г.
- Словарь алгоритмов и структур данных NIST: код Грея.
- Hitch Hiker's Guide по эволюционным вычислениям, Q21: Что такое коды Грея и почему они используются?, включая C код для преобразования между двоичным и BRGC.
- Драгос А. Харабор использует Коды Грея в 3D-дигитайзере.
- Однодорожечные коды Грея, двоичные цепные коды (Ланкастер 1994), и регистры сдвига с линейной обратной связью все они полезны для определения абсолютного положения на одноколейном поворотном энкодере (или другом датчике положения).
- Столбец AMS: коды Грея
- Генератор колеса оптического кодировщика
- ProtoTalk.net - Понимание квадратурного кодирования - Более подробно описывает квадратурное кодирование с акцентом на роботизированные приложения