WikiDer > Большой дизнуб диргомбидодекаэдр
| Большой дизнуб диргомбидодекаэдр | |
|---|---|
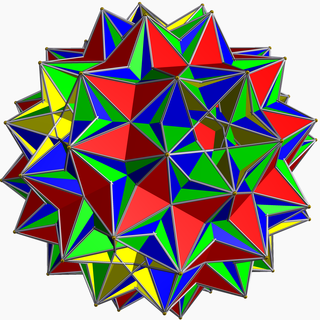 | |
| Тип | Равномерный звездный многогранник |
| Элементы | F = 204, E = 360 V = 60 (χ = −96) |
| Лица по сторонам | 120{3}+60{4}+24{5/2} |
| Символ Wythoff | | (3/2) 5/3 (3) 5/2 |
| Группа симметрии | ячас, [5,3], *532 |
| Указатель ссылок | U-, C-, W- |
| Двойной многогранник | Великий дизнуб дирхомбидодекакрон |
| Фигура вершины |  (5/2.4.3.3.3.4. 5/3.4.3/2.3/2.3/2.4)/2 |
| Акроним Bowers | Гидисдрид |
В геометрия, то большой дизнуб диргомбидодекаэдр, также называемый Фигура Скиллинга, является вырожденным однородный звездный многогранник.
В 1970 году было доказано, что их всего 75 равномерные многогранники кроме бесконечных семейств призмы и антипризмы. Джон Скиллинг открыл еще один вырожденный пример, большой диромбидодекаэдр disnub, ослабив условие, что края должны быть единственными. Точнее, он позволял любому четному количеству граней встречаться на каждом краю до тех пор, пока набор граней не мог быть разделен на два связанных набора (Skilling, 1975). Из-за своей геометрической реализации, имеющей несколько двойных ребер, где встречаются 4 грани, он считается выродиться однородный многогранник, но не строго однородный многогранник.
Количество ребер неоднозначно, потому что лежащий в основе абстрактный многогранник имеет 360 ребер, но 120 пар из них имеют одинаковое изображение в геометрической реализации, так что геометрическая реализация имеет 120 одинарных ребер и 120 двойных ребер, где встречаются 4 грани, для всего 240 граней. Эйлерова характеристика абстрактного многогранника равна −96. Если пары совпадающих ребер в геометрической реализации считать одиночными, то у нее всего 240 ребер и эйлерова характеристика 24.
В вершина фигуры имеет 4 квадрат грани, проходящие через центр модели.
Его можно построить как Эксклюзивный или (смесь) большой диромбикосододекаэдр и соединение двадцати октаэдров.
Связанные многогранники
Он разделяет то же самое расположение кромок как большой диромбикосододекаэдр, но имеет другой набор треугольных граней. Вершины и ребра также являются общими с однородными соединениями двадцать октаэдров или же двадцать тетрагемигексаэдров. 180 кромок общие с большой курносый додецикосододекаэдр.
 Выпуклый корпус |  Большой курносый додецикосододекаэдр |  Большой диромбикосододекаэдр |
 Большой дизнуб диргомбидодекаэдр |  Соединение двадцати октаэдров |  Соединение двадцати тетрагемигексаэдров |
Двойной многогранник
В двойной из большой дизнуб диргомбидодекаэдр называется великий диснуб дирхомбидодекакрон. Это невыпуклый бесконечный равногранный многогранник.
Как визуально идентичный великий диромбикосидодекакрон в Магнус Веннингерс Двойные модели, он представлен пересекающимися бесконечными призмы проходя через центр модели, срежьте в удобном для производителя месте. Веннингер предположил, что эти фигуры принадлежат к новому классу людей. звездчатость многогранники, называемые звёздчатость до бесконечности. Однако он также признал, что, строго говоря, они не являются многогранниками, потому что их конструкция не соответствует обычным определениям.
Галерея
 Традиционная начинка | 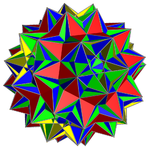 Заполнение по модулю-2 |
Смотрите также
Рекомендации
- Скиллинг, Джон (1975), "Полный набор однородных многогранников", Философские труды Королевского общества A, 278 (1278): 111–135, Дои:10.1098 / рста.1975.0022.
- Вайсштейн, Эрик В. «Большой диромбикосододекаэдр». MathWorld.
- http://www.software3d.com/MillersMonster.php