WikiDer > Метод Халлады

Синус, косинус и версин θ в единицах круга с центром в О

В Метод Халлады, разработанный французом Эмилем Халладом, представляет собой метод, используемый в геометрия трека за геодезия, проектирование и нанесение кривых в Железнодорожный отслеживать.^[1]

Он включает в себя измерение смещения линии струны от внешней стороны кривой в центральной точке аккорд. На самом деле струна слишком толстая, чтобы обеспечить четкое чтение, и легко ломается при натяжении, необходимом для минимизации движения из-за ветра. Вместо этого можно использовать катушку с проволокой со специальными держателями (вилками Hallade) для удержания проволоки на фиксированном расстоянии от рельса. Измерения производятся с помощью правила Халлада, специальной линейки, нулевая точка которой совпадает со смещением вилок, тем самым отменяя его. Назначение смещения - обеспечить небольшие отрицательные измерения. Без этого геодезистам часто приходилось бы читать с обеих сторон рельса, чтобы определять правильные значения на прямых участках пути, которые обычно представляют собой смесь небольших положительных и отрицательных версий.

Используется стандартная длина хорды: в Великобритании условно 30 метров, а иногда и 20 метров. Половина аккорды, то есть интервалы 15 метров или 10 метров, обозначены на базовой железной дороге с использованием мела. Затем струну, которая составляет один полный аккорд, натягивают таким образом, чтобы один конец был на двух отметках на каждом конце аккорда, и измеряется смещение на отметке половины аккорда.

В Версина хорды, равной этому измеренному значению смещения, можно рассчитать, используя аппроксимацию:

${ displaystyle operatorname {versin} theta = 1-cos , theta}$

который:

${ Displaystyle v приблизительно { гидроразрыва {L ^ {2}} {8r}}}$

куда
${ displaystyle v}$ = версия (м),
${ displaystyle L}$ = длина хорды (м),
${ displaystyle r}$ = радиус кривой (м)

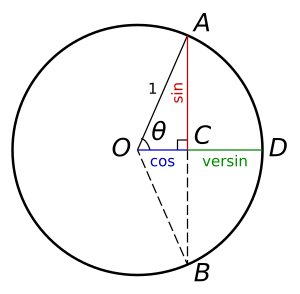
Эта формула верна и для других единиц измерения, таких как футы. Отношения версины, хорды и радиуса выводятся из теорема Пифагора. Исходя из схемы справа:

${ displaystyle OC = { sqrt {OA ^ {2} -AC ^ {2}}}}$

Мы можем заменить OC на r (радиус) минус v, OA на r и AC на L / 2 (половину хорды). Затем измените формулу на:

${ displaystyle r-v = { sqrt {r ^ {2} - ({ frac {L} {2}}) ^ {2}}},}$

${ displaystyle r ^ {2} -2rv + v ^ {2} = r ^ {2} - ({ frac {L} {2}}) ^ {2},}$

${ displaystyle 2r-v = { frac {L ^ {2}} {4v}},}$

${ displaystyle r = { frac {L ^ {2}} {8v}} + { frac {v} {2}}.}$

Поскольку изогнутые дорожки обычно большие, результат v / 2 очень мал. Чтобы упростить формулу, приближение:

${ Displaystyle г приблизительно { гидроразрыва {L ^ {2}} {8v}}}$

Следующее может использоваться, чтобы найти версию заданной кривой постоянного радиуса:^[2]

${ Displaystyle v приблизительно { гидроразрыва {L ^ {2}} {8r}}}$

Метод Халлады заключается в использовании хорды для непрерывного измерения версины с наложением рисунка вдоль кривой. Значения версины для идеальной круговой кривой будут иметь такое же число.^[3] Сравнивая обследованные фигуры версина с дизайнерскими версиями, это затем можно использовать для определения того, что шлюзы следует применить к дорожке, чтобы кривая была правильно выровнена. Часто это делается с помощью колышков, которые вбиваются в землю в снимать рядом с направляющей, которую нужно выровнять. Процесс установки колышков в правильное положение известен как `` разметка ''. Если кривая должна иметь желаемый постоянный радиус, который обычно определяется физическими препятствиями и степенью косяк что разрешено, версину можно рассчитать для желаемого радиуса, используя это приближение. На практике многие кривые пути являются переходными кривыми и поэтому имеют изменяющиеся радиусы. Чтобы сохранить плавный переход, различия в версиях между последовательными полуаккордами измеряются и сводятся к минимуму.

В Обзор Hallade это метод съемки, который использует тот же принцип для измерения версин вдоль существующей кривой. На основе значений версины радиус этой круговой криволинейной дорожки может быть приблизительно равен:^[4]

${ Displaystyle г приблизительно { гидроразрыва {L ^ {2}} {8v}}}$

Этот метод можно выполнить вручную, и этот метод до сих пор используется в Великобритании. Однако из-за сложности вычислений на больших участках пути теперь это часто выполняется компьютером,^[5] при этом данные о геометрии трека загружаются прямо в управляемый компьютером трамбовочно-футеровочная машина для реализации.

Смотрите также

• Геометрия трека
• Автомобиль геометрии трассы

Рекомендации

внешняя ссылка

• Система Hallade
• Железнодорожные инженеры