WikiDer > Катушка Гельмгольца

Helmholtz coil

Катушка Гельмгольца

Схема катушки Гельмгольца

А Катушка Гельмгольца это устройство для создания области почти однородной магнитное поле, названный в честь немецкого физика Герман фон Гельмгольц. Он состоит из двух электромагниты на той же оси. Помимо создания магнитных полей, катушки Гельмгольца также используются в научных приборах для подавления внешних магнитных полей, таких как магнитное поле Земли.

Пучок катодных лучей в вакуумной лампе, изогнутый в круг катушкой Гельмгольца

Описание

Пара Гельмгольца состоит из двух идентичных круглых магнитных катушек, которые расположены симметрично вдоль общей оси, по одной с каждой стороны экспериментальной зоны и разделенных расстоянием ${ displaystyle h}$ равный радиусу ${ displaystyle R}$ катушки. Каждая катушка несет равную электрический ток в том же направлении.^[1]

Настройка ${ displaystyle h = R}$ , что и определяет пару Гельмгольца, сводит к минимуму неоднородность поля в центре катушек в том смысле, что ${ Displaystyle partial ^ {2} B / partial x ^ {2} = 0}$ ^[2] (это означает, что первая ненулевая производная равна ${ Displaystyle partial ^ {4} B / partial x ^ {4}}$ как объяснено ниже), но оставляет около 7% различия в напряженности поля между центром и плоскостями катушек. ${ displaystyle h}$ уменьшает разницу в поле между центром и плоскостями катушек за счет ухудшения однородности поля в области около центра, как измерено ${ Displaystyle partial ^ {2} B / partial x ^ {2}}$ .^[3]

В некоторых приложениях катушка Гельмгольца используется для компенсации Магнитное поле Земли, создавая область с напряженностью магнитного поля, намного близкой к нулю.^[4]

Математика

Силовые линии магнитного поля в плоскости, разделяющей токовые петли пополам. Обратите внимание, что поле между парой катушек примерно однородно. (На этом рисунке катушки расположены одна рядом с другой: ось горизонтальна.)

Индукция магнитного поля вдоль оси, пересекающей центр катушек; z = 0 - точка посередине расстояния между витками

Контуры, показывающие величину магнитного поля около пары катушек, одна катушка находится вверху, а другая внизу. Внутри центрального «осьминога» поле находится в пределах 1% от его центрального значения. B₀. Восемь контуров соответствуют величине поля 0,5B₀, 0.8 B₀, 0.9 B₀, 0.95 B₀, 0.99 B₀, 1.01 B₀, 1.05 B₀, и 1.1B₀.

Расчет точного магнитного поля в любой точке пространства математически сложен и включает изучение Функции Бесселя. По оси катушечной пары дело обстоит проще, и удобно думать о Серия Тейлор разложение напряженности поля как функции ${ displaystyle x}$ - расстояние от центральной точки пары катушек вдоль оси. В силу симметрии члены нечетного порядка в разложении равны нулю. Расположив катушки так, чтобы начало координат ${ displaystyle x = 0}$ является точка перегиба для напряженности поля, обусловленной каждой катушкой в отдельности, можно гарантировать, что порядок ${ displaystyle x ^ {2}}$ член также равен нулю, и, следовательно, старший непостоянный член имеет порядок ${ displaystyle x ^ {4}}$ . Точка перегиба для простой катушки расположена по оси катушки на расстоянии ${ displaystyle R / 2}$ от его центра. Таким образом, места для двух катушек ${ Displaystyle х = pm R / 2}$ .

Приведенный ниже расчет дает точное значение магнитного поля в центральной точке. Если радиус р, количество витков в каждой катушке равно п и ток через катушки я, то магнитное поле B в середине между катушками будет равно

{ displaystyle B = { left ({ frac {4} {5}} right)} ^ {3/2} { frac { mu _ {0} nI} {R}},}

где ${ displaystyle mu _ {0}}$ это проницаемость свободного пространства ( ${ displaystyle 4 pi times 10 ^ {- 7} { text {T}} cdot { text {m / A}}}$ ).

Вывод

Начните с формулы для поля на оси из-за однопроводной петли, которая сама получена из Закон Био – Савара:^[5]

{ displaystyle B_ {1} (x) = { frac { mu _ {0} IR ^ {2}} {2 (R ^ {2} + x ^ {2}) ^ {3/2}}} .}

Вот

{ displaystyle mu _ {0} ;}

= the постоянная проницаемости =

{ displaystyle 4 pi times 10 ^ {- 7} { text {T}} cdot { text {m / A}} = 1,257 times 10 ^ {- 6} { text {T}} cdot { text {m / A}},}

{ Displaystyle I ;}

= ток катушки, дюйм амперы,

{ Displaystyle R ;}

= радиус рулона, в метрах,

{ Displaystyle х ;}

= расстояние катушки по оси до точки в метрах.

Катушки Гельмгольца состоят из п витков провода, поэтому эквивалентный ток в однооборотной катушке равен п раз больше текущего я в п-поворот катушки. Подстановка nI для я в приведенной выше формуле дает поле для п-поворотная катушка:

{ displaystyle B_ {1} (x) = { frac { mu _ {0} nIR ^ {2}} {2 (R ^ {2} + x ^ {2}) ^ {3/2}}} .}

В катушке Гельмгольца точка на полпути между двумя петлями имеет Икс значение, равное R / 2, поэтому рассчитайте напряженность поля в этой точке:

{ displaystyle B_ {1} left ({ frac {R} {2}} right) = { frac { mu _ {0} nIR ^ {2}} {2 left (R ^ {2} + left ({ frac {R} {2}} right) ^ {2} right) ^ {3/2}}}.}

Здесь также две катушки вместо одной (катушка выше находится на Икс= 0; есть вторая катушка на Икс=р). Из-за симметрии напряженность поля в средней точке будет вдвое больше, чем значение одиночной катушки:

{ displaystyle { begin {align} B left ({ frac {R} {2}} right) & = 2B_ {1} left ({ frac {R} {2}} right) & = { frac {2 mu _ {0} nIR ^ {2}} {2 left (R ^ {2} + left ({ frac {R} {2}} right) ^ {2} right) ^ {3/2}}} = { frac { mu _ {0} nIR ^ {2}} { left (R ^ {2} + left ({ frac {R} {2}) } right) ^ {2} right) ^ {3/2}}} & = { frac { mu _ {0} nIR ^ {2}} { left (R ^ {2} + { frac {1} {4}} R ^ {2} right) ^ {3/2}}} = { frac { mu _ {0} nIR ^ {2}} { left ({ frac { 5} {4}} R ^ {2} right) ^ {3/2}}} & = { left ({ frac {4} {5}} right)} ^ {3/2} { frac { mu _ {0} nI} {R}} & = { left ({ frac {8} {5 { sqrt {5}}}} right)} { frac { mu _ {0} nI} {R}}. конец {выровнено}}}

Изменяющееся во времени магнитное поле

В большинстве катушек Гельмгольца используется постоянный (постоянный) ток для создания статического магнитного поля. Для многих приложений и экспериментов требуется изменяющееся во времени магнитное поле. Эти приложения включают в себя тесты восприимчивости к магнитному полю, научные эксперименты и биомедицинские исследования (взаимодействие между магнитным полем и живой тканью). Требуемые магнитные поля обычно являются импульсными или непрерывными синусоидальными волнами. Диапазон частот магнитного поля может составлять от около 0 Гц до многих килогерц или даже мегагерц (МГц). Драйвер катушки Гельмгольца переменного тока необходим для создания необходимого изменяющегося во времени магнитного поля. Драйвер усилителя сигнала должен быть способен выдавать высокий переменный ток для создания магнитного поля.

Напряжение и ток драйвера

Используйте приведенное выше уравнение в разделе математики, чтобы рассчитать ток катушки для желаемого магнитного поля, $B$ .

${ displaystyle I = left ({ frac {5} {4}} right) ^ {3/2} left ({ frac {BR} { mu _ {0} n}} right)}$

где ${ displaystyle mu _ {0}}$ проницаемость свободного пространства или ${ displaystyle 4 pi times 10 ^ {- 7} { text {T}} cdot { text {m / A}} = 1,257 times 10 ^ {- 6} { text {T}} cdot { text {m / A}},}$

${ Displaystyle I ;}$ = ток катушки, в амперах,

${ Displaystyle R ;}$ = радиус рулона, в метрах,

n = количество витков в каждой катушке.

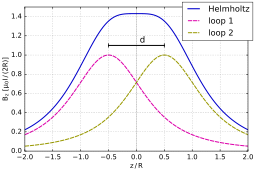
Использование функционального генератора и драйвера усилителя сильноточного сигнала для генерации высокочастотного магнитного поля Гельмгольца

Затем рассчитайте необходимое напряжение усилителя драйвера катушки Гельмгольца:^[6]

{ displaystyle V = I { sqrt {{ bigl [} omega { bigl (} L_ {1} + L_ {2} { bigr)} { bigr]} ^ {2} + { bigl ( } R_ {1} + R_ {2} { bigr)} ^ {2}}}}

где

$я$ пиковый ток,
$ω$ угловая частота или $ω = 2 πf$ ,
$L 1$ и $L 2$ индуктивности двух катушек Гельмгольца, и
$р 1$ и $р 2$ - сопротивления двух катушек.

Высокочастотный последовательный резонансный

Создать статическое магнитное поле относительно легко; сила поля пропорциональна току. Создать высокочастотное магнитное поле сложнее. Катушки представляют собой катушки индуктивности, и их сопротивление увеличивается пропорционально частоте. Для обеспечения такой же напряженности поля на удвоенной частоте требуется удвоенное напряжение на катушке. Вместо прямого возбуждения высокого напряжения на катушку можно использовать последовательный резонансный контур для обеспечения высокого напряжения.^[7] Последовательный конденсатор добавлен последовательно с катушками. Емкость выбирается так, чтобы катушка резонировала на желаемой частоте. Остается только паразитное сопротивление катушек. Этот метод работает только на частотах, близких к резонансной частоте; для генерации поля на других частотах требуются другие конденсаторы. Резонансная частота катушки Гельмгольца, ${ displaystyle f_ {0}}$ , и емкость конденсатора C приведены ниже.^[6]

{ displaystyle f_ {0} = { frac {1} {2 pi { sqrt { left (L_ {1} + L_ {2} right) C}}}}}

{ displaystyle C = { frac {1} { left (2 pi f right) ^ {2} left (L_ {1} + L_ {2} right)}}}

Катушки Максвелла

Катушки Гельмгольца (обручи) на трех перпендикулярных осях, используемых для подавления магнитного поля Земли внутри вакуумного резервуара в эксперименте с электронным пучком 1957 года.

Чтобы улучшить однородность поля в пространстве внутри катушек, можно добавить дополнительные катушки снаружи. Джеймс Клерк Максвелл показал в 1873 году, что третья катушка большего диаметра расположена на полпути между двумя катушками Гельмгольца с расстоянием между катушками, увеличенным от радиуса катушки. ${ displaystyle R}$ к ${ displaystyle { sqrt {3}} R}$ может уменьшить дисперсию поля на оси до нуля до шестой производной позиции. Иногда это называют Катушка Максвелла.

Смотрите также

Соленоид
Массив Хальбаха
А магнитная бутылка имеет ту же структуру, что и катушки Гельмгольца, но с магнитами, разнесенными дальше друг от друга, так что поле расширяется в середине, захватывая заряженные частицы с расходящимися силовыми линиями. Если одна катушка перевернута, она производит ловушка острия, который также захватывает заряженные частицы.^[8]
Катушки Гельмгольца были разработаны и изготовлены для Армейская исследовательская лаборатория лаборатория электромагнитных испытаний композитов в 1993 году для испытаний композитных материалов в низкочастотных магнитных полях.^[9]

использованная литература

^ Рамсден, Эдвард (2006). Датчики на эффекте Холла: теория и приложения (2-е изд.). Амстердам: Elsevier / Newnes. п. 195. ISBN 978-0-75067934-3.
^ Катушка Гельмгольца в блоках СГС В архиве 24 марта 2012 г. Wayback Machine
^ Электромагнетизм
^ «Магнитометр поля Земли: катушка Гельмгольца» Ричард Вотиз 2004 В архиве 28 июня 2007 г., г. Archive.today
^ http://hyperphysics.phy-astr.gsu.edu/HBASE/mintage/curloo.html#c3
^ ^а ^б Ян, KC. «Высокочастотные катушки Гельмгольца генерируют магнитные поля». EDN. Получено 2016-01-27.
^ «Высокочастотная резонансная электромагнитная катушка». www.accelinstruments.com. Получено 2016-02-25.
^ http://radphys4.c.u-tokyo.ac.jp/asacusa/wiki/index.php?Cusp%20trap
^ Джей, ДеТрой, Дэвид; Дж., Чейз, Рональд (ноябрь 1994 г.). «Расчет и измерение полей катушки Гельмгольца». Цитировать журнал требует | журнал = (Помогите)

внешние ссылки

Осевое поле идеальной катушки Гельмгольца.
Осевое поле реальной пары катушек Гельмгольца
Поля катушек Гельмгольца Франц Крафт, Демонстрационный проект Wolfram.
Кевин Кунс (2007) Расчет магнитного поля внутри плазменной камеры, использует эллиптические интегралы и их производные для вычисления внеосевых полей, от PBworks.
ДеТрой, Дэвид Дж .; Чейз, Рональд Дж. (Ноябрь 1994 г.), Расчет и измерение полей катушки Гельмгольца. (PDF), Армейская исследовательская лаборатория, ARL-TN-35
Магнитные поля катушек
http://physicsx.pr.erau.edu/HelmholtzCoils/

[1] Рамсден, Эдвард (2006). Датчики на эффекте Холла: теория и приложения (2-е изд.). Амстердам: Elsevier / Newnes. п. 195. ISBN 978-0-75067934-3.

[2] Катушка Гельмгольца в блоках СГС В архиве 24 марта 2012 г. Wayback Machine

[3] Электромагнетизм

[4] «Магнитометр поля Земли: катушка Гельмгольца» Ричард Вотиз 2004 В архиве 28 июня 2007 г., г. Archive.today

[5] ttp://hyperphysics.phy-astr.gsu.edu/HBASE/mintage/curloo.html#c3

[:0-6] а ^б Ян, KC. «Высокочастотные катушки Гельмгольца генерируют магнитные поля». EDN. Получено 2016-01-27.

[7] «Высокочастотная резонансная электромагнитная катушка». www.accelinstruments.com. Получено 2016-02-25.

[8] ttp://radphys4.c.u-tokyo.ac.jp/asacusa/wiki/index.php?Cusp%20trap

[9] Джей, ДеТрой, Дэвид; Дж., Чейз, Рональд (ноябрь 1994 г.). «Расчет и измерение полей катушки Гельмгольца». Цитировать журнал требует | журнал = (Помогите)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

Navigation