WikiDer > История индуистско-арабской системы счисления
| Системы счисления |
|---|
| Индусско-арабская система счисления |
| Восточная Азия |
| Европейский |
| Американец |
| По алфавиту |
| Бывший |
| Позиционные системы к основание |
| Нестандартные позиционные системы счисления |
| Список систем счисления |
В Индусско-арабская система счисления это десятичная дробь номинальная стоимость система счисления, в которой используется нуль глиф как в «205».[1]
Его символы произошли от индийского Цифры брахми. Полная система возникла в 8-9 веках и впервые описана за пределами Индии в Аль-Хорезмис О вычислении с помощью индусских цифр (ок. 825), а второй Аль-Киндичетырехтомник Об использовании индийских цифр (ок. 830).[2] Сегодня имя Индусско-арабские цифры обычно используется.
Десятичная система
Историки прослеживают современные цифры в большинстве языков до Цифры брахми, которые использовались примерно в середине III века до нашей эры.[3] В размещаемая стоимость Система, однако, была разработана позже. Цифры брахми были найдены в надписях в пещерах и на монетах в регионах, близких к Пуна, Махараштра[2] и Уттар-Прадеш в Индии. Эти цифры (с небольшими вариациями) использовались до 4 века.[3]
Вовремя Период Гупта (с начала 4-го века до конца 6-го века), цифры Гупта произошли от цифр Брахми и были распространены на больших территориях империей Гуптов, когда они завоевали территорию.[3] Примерно с 7 века цифры Гупта превратились в цифры Нагари.
Развитие в Индии
Вовремя Ведический период (1500–500 гг. До н.э.), мотивированное геометрическим построением огненных алтарей и астрономией, использованием числовой системы и основных математических операций, разработанных в северной Индии.[4][5] Индуистская космология требовала владения очень большими числами, такими как калпа (время жизни Вселенной) составляет 4 320 000 000 лет, а "небесная орбита" - 18 712 069 200 000 000 лет. йоджанас.[6] Числа были выражены с использованием "обозначения именованных разрядов", с использованием имен для степеней 10, например даша, шатха, сахасра, Аюта, Ниюта, прайута, арбуда, Ньярбуда, самудра, мадхья, анта, парардха и т. д., последний из которых является названием триллиона (1012).[7] Например, число 26 432 было выражено как "2 Аюта, 6 сахасра, 4 шатха, 3 даша, 2."[8] В буддийском тексте Лалитавистара, Будда рассказал схему чисел до 1053.[9][10]
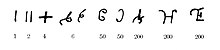
Форма цифр в Ашоканадписи в Брахми письменность (середина III века до н.э.) включала отдельные знаки для чисел от 1 до 9, от 10 до 90, 100 и 1000. Кратное 100 или 1000 представлялось модификацией (или «шифрованием»)[11]) знака числа, используя знак числа множителя.[12] Такие зашифрованные числа непосредственно представляли именованные числовые значения, используемые в устной форме. Они продолжали использоваться в надписях до конца IX века.
В своем основополагающем тексте 499 г. н.э. Арьябхата разработал новую позиционную систему счисления, используя санскритские согласные для малых чисел и гласные для степеней 10. Используя эту систему, числа до миллиарда можно было выразить короткими фразами, например. грамм., khyu-ghṛ что представляет собой число 4,320,000. Система не прижилась, потому что она генерировала довольно труднопроизносимые фразы, но она, возможно, привела в действие принцип позиционной системы счисления (называемый даша-гуноттара, показатель степени 10) математикам более позднего возраста.[13] Более элегантный Катапаяди Схема была разработана в более поздние века и представляет собой систему счисления, включающую ноль.[14]
Числовые значения без нуля

В то время как числительные в текстах и надписях использовали обозначения с именованными позициями, в расчетах можно было использовать более эффективные обозначения, возможно, начиная с I века нашей эры. Расчеты проводились на глиняных табличках, покрытых тонким слоем песка, в результате чего возник термин дхули-карана ("песочная работа") для более высоких вычислений. Карл Меннингер считает, что в таких вычислениях они должны были отказаться от зашифрованных цифр и записать только последовательности цифр для представления чисел. Ноль был бы представлен как «недостающее место», например точка.[15] Единственная доступная нам рукопись с проработанными примерами, Бахшалинская рукопись (с неясной датой) использует разрядную систему с точкой для обозначения нуля. Точка получила название шунья-стхана, "пустое место". Этот же символ также использовался в алгебраических выражениях для неизвестного (как в каноническом Икс в современной алгебре).[16]
Текстовые упоминания о системе ценностей наблюдаются с V века нашей эры. Буддийский философ Васубандху в V веке говорится: «Когда [одна и та же] глиняная счетная деталь находится вместо единиц, она обозначается как единица, а в сотнях - сотня». Комментарий к Патанджалис Йога-сутры из V века гласит: «Как строка в разряде сотен [означает] сто, в десятках - десять и одна в разряде единиц, так одну и ту же женщину называют матерью, дочерью и сестрой».[17]
Система под названием бхута-санкхйа («номера объектов» или «конкретные числа») использовались для представления чисел в санскритских стихах с использованием концепции, представляющей цифру для обозначения самой цифры. Джайнский текст под названием Локавибхага, датированный 458 г. н.э.,[18] упоминает объективированную цифру
"панчабхйах кхалу шунйебхйах парам двэ сапта чамбарам экам трини ча рупам ча"
что означает «пять пустот, затем две и семь, небо, одна и три и форма», то есть число 13107200000.[19][20] Такие объективированные числа широко использовались начиная с VI века, особенно после Варахамихира (c. 575 г. н.э.). Ноль явно представлен в таких числах, как «пустота» (Сунья) или "небо-космос" (амбара акаша).[21] Соответственно, точка, используемая вместо нуля в письменных цифрах, называлась шунья-бинду.[22]
Числовые значения с нулем
В 628 году н.э. астроном-математик Брахмагупта написал свой текст Брахма Сфута Сиддханта который содержал первую математическую трактовку нуля. Он определил ноль как результат вычитания числа из самого себя, постулировал отрицательные числа и обсудил их свойства в рамках арифметических операций. Его слово для нуля было шунья (недействительно), тот же термин, который ранее использовался для обозначения пустого места в 9-значной системе счисления.[25] Это дало новый взгляд на шунья-бинду как число и проложили путь к возможной эволюции нулевой цифры. Точка продолжала использоваться в течение как минимум 100 лет после этого и была передана в Юго-Восточную Азию и Аравию. Кашмирский Скрипт шарада до сего дня сохранила нулевую точку.
К концу 7 века десятичные числа начинают появляться в надписях в Юго-Восточной Азии, а также в Индии.[22] Некоторые ученые считают, что они появились еще раньше. Часто цитируется грант из медной пластины VI века в Манкани с цифрой 346 (соответствует 594 году н. Э.).[26] Но его надежность вызывает споры.[22][27] Первое неоспоримое появление 0 в надписи происходит при Гвалиор в 876 г. н.э., содержащий цифру «270» в обозначениях, удивительно похожих на наши.[28] На протяжении 8-го и 9-го веков использовались как старые цифры Брахми, так и новые десятичные числа, иногда появляющиеся в одних и тех же надписях. В некоторых документах рассматривается переходный период около 866 г. н.э.[22]
Принятие арабами
Перед подъемом Халифат, индуистско-арабская система счисления уже продвигалась на Запад и упоминалась в Сирия в 662 г. Несторианский ученый Северус Себохт который написал следующее:
- "Я опущу все обсуждения науки индейцев ... их тонких открытий в астрономии, открытий, которые более гениальны, чем у греков и вавилонян, и их ценных методов расчетов, которые превосходят описание. I Я хочу только сказать, что это вычисление производится с помощью девяти знаков. Если те, кто верит, потому что они говорят по-гречески, что они достигли пределов науки, прочитают индийские тексты, они будут убеждены, даже если немного в конце дня, что есть другие, кто знает что-то ценное ".[2]
Согласно с Аль-Кифтис История образованных людей [3]:
- «... человек из Индии предстал перед халифом аль-Мансуром в году [776 г. н.э.], который хорошо разбирался в методе расчета сиддханта, связанном с движением небесных тел, и имел способы расчета уравнений, основанных на полухорда [по сути, синус], рассчитанная в половинных градусах ... Все это содержится в работе ... из которой он утверждал, что взял полухорду, рассчитанную для одной минуты. Аль-Мансур приказал этой книге быть переведенным на арабский язык, и произведение должно быть написано на основе перевода, чтобы дать Арабов прочная база для расчета движения планет ... "
Работа, скорее всего, была Брахмагуптас Брахма Сфута Сиддханта (Ифрах) [4] (Открытие Вселенной), написанное в 628 г. [5]. Независимо от того, прав ли Ифра, поскольку все индийские тексты после Арьябхатас Арьябхатия использовали индийскую систему счисления, разумеется, с этого времени у арабов был перевод текста, написанного в индийской системе счисления. [6]
В его тексте Арифметика Аль-Уклидиси (Дордрехт: Д. Рейдел, 1978), В КАЧЕСТВЕ. СаиданИсследования не смогли полностью ответить, как цифры попали в арабский мир:
- "Кажется правдоподобным, что он постепенно дрейфовал, вероятно, до VII века, по двум каналам, один из которых начинался от Синда, подвергался персидской фильтрации и распространялся на территории, которая сейчас известна как Ближний Восток, а другой начинался с берегов Индийский океан и простирается до южного побережья Средиземного моря ».[7]
Аль-Уклидиси разработал обозначение для представления десятичных дробей.[29][30]Цифры получили известность благодаря их использованию в основной работе Персидский математик Аль-Хорезми, чья книга О вычислении с помощью индусских цифр было написано около 825 г., а Араб математик Аль-Кинди, который написал четыре тома (см. [2]) «Об использовании индийских цифр» (Ketab fi Isti'mal al-'Adad al-Hindi) около 830 г. Они, среди других работ, способствовали распространению индийского система счисления в Средний Восток и Запад.
Разработка символов
Развитие числительных в ранней Европе показано ниже:
Счеты в сравнении с индуистско-арабской системой счисления на изображениях раннего Нового времени
Усыновление в Европе
- 976. Первые арабские цифры в Европе появились в Кодекс Виджиланус в 976 году.
- 1202. Фибоначчи, Итальянский математик, учившийся в Béjaïa (Буги), Алжир, продвигал арабскую систему счисления в Европа с его книгой Liber Abaci, который был опубликован в 1202 году.
- 1482. Однако эта система не получила широкого распространения в Европе до изобретения печать. (См., Например, Карта мира Птолемея 1482 года напечатано Линхарт Холле в Ульме и другие примеры в Музей Гутенберга в Майнц, Германия.)
- 1549. Это правильный формат и последовательность "современные числа"на титульном листе" Libro Intitulado Arithmetica Practica "автора Хуан де Исиар, баскский каллиграф и математик, Сарагоса 1549.
За последние несколько столетий европейская разновидность арабских чисел распространилась по всему миру и постепенно стала наиболее часто используемой системой счисления в мире.
Даже во многих странах в языках, имеющих свои собственные системы счисления, европейские арабские цифры широко используются в коммерция и математика.
Влияние на арифметику
Значение развития позиционной системы счисления описывает французский математик. Пьер Симон Лаплас (1749–1827), который писал:
Именно Индия дала нам гениальный метод выражения всех чисел с помощью десяти символов, при этом каждому символу присваивается значение положения, а также абсолютное значение; глубокая и важная идея, которая сейчас кажется нам настолько простой, что мы игнорируем ее истинные достоинства, но сама ее простота, большая легкость, которую она придавала всем вычислениям, ставит нашу арифметику на первое место среди полезных изобретений, и мы будем признательны величие этого достижения, если вспомнить, что он ускользнул от гения Архимед и Аполлоний, два из величайших умов древности.[31]
Смотрите также
Примечания
- ^ «Индусско-арабские цифры». Архивировано из оригинал на 2005-12-27. Получено 2005-12-13.
- ^ а б "Абу Юсуф Якуб ибн Исхак ас-Саббах аль-Кинди". Архивировано из оригинал на 2007-10-26. Получено 2007-01-12.
- ^ а б c Джон Дж. О'Коннор и Эдмунд Ф. Робертсон (ноябрь 2000 г.). «Индийские цифры». Архив истории математики MacTutor. Архивировано из оригинал на 2015-07-06. Получено 2007-07-24.
- ^ Смит и Карпински, 2013 г.С. 12–15.
- ^ Плофкер 2009, Гл. 2.
- ^ Плофкер 2009С. 68–69.
- ^ Плофкер 2009, п. 14.
- ^ Меннингер 2013, п. 397.
- ^ Смит и Карпински, 2013 г., п. 15.
- ^ Плофкер 2009, п. 57.
- ^ Меннингер 2013, п. 395.
- ^ Плофкер 2009, п. 44.
- ^ Плофкер 2009С. 73–75.
- ^ Плофкер 2009С. 75–77.
- ^ Меннингер 2013, п. 398.
- ^ Сарасвати и Джйотишмати 1979С. 27, 66.
- ^ Плофкер 2009, п. 46.
- ^ Ифрах 1998, п. 417.
- ^ Ифрах 1998, п. 416.
- ^ Утверждалось, что текст середины III века н.э. Явана-джатака (по "греческому гороскопу") использовал прием бхута-санкхьи (Плофкер 2009, п. 47). Но сейчас это считается ошибкой интерпретации. (Мак, Билл М. (2013), «Передача греческой астральной науки в Индию. Пересмотренные критические замечания по содержанию и недавно обнаруженному манускрипту Яванаджатаки», История науки в Южной Азии, 1: 1–20, Дои:10.18732 / H2RP4T, заархивировано из оригинал на 2016-06-04)
- ^ Смит и Карпински, 2013 г., Гл. III; Ифрах 1998, стр. 411–418; Меннингер 2013, п. 398
- ^ а б c d Саломон, Ричард (1998), Индийская эпиграфия: руководство по изучению надписей на санскрите, пракрите и других индоарийских языках, Oxford University Press, США, стр. 61–63, ISBN 978-0-19-535666-3
- ^ Смит, Дэвид Юджин; Карпинский, Луи Чарльз (1911). Индусско-арабские цифры. Бостон, Лондон, Джинн и компания. п. 52.
- ^ Для современного образа: [1]
- ^ Ифрах 1998, п. 439.
- ^ Плофкер 2009, п. 45.
- ^ Шастри, Аджая Митра (1998), «Манканская хартия Тараласвами и древность десятичной системы счисления», Летопись Института восточных исследований Бхандаркара, 79 (1/4): 161–170, JSTOR 41694535
- ^ Плофкер 2009, стр. 45–46; Меннингер 2013, стр. 396–397; Ифрах 1998, п. 400
- ^ Биография Аль-Уклидиси Дж. Дж. О'Коннор и Э. Ф. Робертсон
- ^ Самые ранние случаи использования символов дробей Джефф Миллер
- ^ Кумар, Радж (2003). Очерки Древней Индии. Издательство Discovery. С. 196–. ISBN 978-81-7141-682-0.
- Источники
- Ifrah, Georges (1998) [впервые опубликовано на французском языке в 1981 году], Всеобщая история чисел: от предыстории до изобретения компьютера, Харвилл, ISBN 978-1-860-46324-2
- Меннингер, Карл (2013) [впервые опубликовано MIT Press в 1969 году], Числовые слова и числовые символы: культурная история чисел, перевод Пола Бронеера, Courier Corporation, ISBN 978-0-486-31977-3
- Плофкер, Ким (2009), Математика в Индии, Издательство Принстонского университета, ISBN 978-0-691-12067-6
- Сарасвати, Свами Сатья Пракаш; Джйотишмати, Уша (1979), Рукопись Бахшали: древний трактат по индийской арифметике (PDF), Аллахабад: Д-р Ратна Кумари Свадхья Санстхан, архив из оригинал (PDF) на 2014-06-20, получено 2016-01-19
- Смит, Д. Э.; Карпинский, Л.С. (2013 г.) [впервые опубликовано в Бостоне, 1911 г.], Индусско-арабские цифры, Дувр, ISBN 978-0486155111
Рекомендации
- «Развитие индуистско-арабской и традиционной китайской арифметики» профессора Лам Лай Йонга, члена Международной академии истории науки
- Индийские цифры Дж. Дж. О'Коннора и Э. Ф. Робертсона
- Арабские цифры Дж. Дж. О'Коннора и Э. Ф. Робертсона
- Индусско-арабские цифры
- Арабская система счисления: Дж. Дж. О'Коннор и Э. Ф. Робертсон.
- Филлиозат, Пьер-Сильвэн (2004), «Математика древнего санскрита: устная традиция и письменная литература», в Chemla, Karine; Коэн, Роберт С .; Ренн, Юрген; и другие. (ред.), История науки, история текста (Бостонская серия по философии науки), Dordrecht: Springer, Нидерланды, 254 страницы, стр. 137–157, Дои:10.1007/1-4020-2321-9_7, ISBN 978-1-4020-2320-0.












