WikiDer > Граф Хоффмана
| Граф Хоффмана | |
|---|---|
 Граф Хоффмана | |
| Названный в честь | Алан Хоффман |
| Вершины | 16 |
| Края | 32 |
| Радиус | 3 |
| Диаметр | 4 |
| Обхват | 4 |
| Автоморфизмы | 48 (Z/2Z × S4) |
| Хроматическое число | 2 |
| Хроматический индекс | 4 |
| Толщина книги | 3 |
| Номер очереди | 2 |
| Характеристики | Гамильтониан[1] Двудольный Идеально Эйлеров |
| Таблица графиков и параметров | |
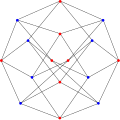
в математический поле теория графов, то Граф Хоффмана это 4-регулярный граф с 16 вершинами и 32 ребрами, обнаруженными Алан Хоффман.[2] Опубликованный в 1963 году, он коспектрально граф гиперкуба Q4.[3][4]
Граф Хоффмана имеет много общих свойств с гиперкубом Q4-оба Гамильтониан и имеют хроматическое число 2, хроматический индекс 4, обхват 4 и диаметр 4. Это также 4-вершинно-связный граф и 4-реберный граф. Однако это не так дистанционно-регулярный. Она имеет толщина книги 3 и номер очереди 2.[5]
Алгебраические свойства
Граф Хоффмана не является вершинно-транзитивный граф а его полная группа автоморфизмов - это группа порядка 48, изоморфная группе прямой продукт из симметричная группа S4 и циклическая группа Z/2Z.
В характеристический многочлен графа Хоффмана равна
сделать это интегральный график- граф, спектр полностью состоит из целых чисел. Это тот же спектр, что и гиперкуб Q4.
Галерея
Граф Хоффмана Гамильтониан.
В хроматическое число графа Хоффмана равно 2.
В хроматический индекс графа Хоффмана равно 4.
Рекомендации
- ^ Вайсштейн, Эрик В. «Гамильтонов граф». MathWorld.
- ^ Вайсштейн, Эрик В. «График Хоффмана». MathWorld.
- ^ Хоффман, А. Дж. «О многочлене графа». Амер. Математика. Месяц 70, 30-36, 1963.
- ^ Ван Дам, Э. Р. и Хемерс, В. Х. "Спектральные характеристики некоторых дистанционно регулярных графов". J. Алгебраический комбинат. 15, 189-202, 2003.
- ^ Джессика Вольц, Инженерные линейные схемы с SAT. Магистерская работа, Тюбингенский университет, 2018 г.