WikiDer > Внутриклассовая корреляция


В статистика, то внутриклассовая корреляция, или коэффициент внутриклассовой корреляции (ICC),[1] это описательная статистика это можно использовать, когда количественные измерения проводятся на единицах, организованных в группы. Он описывает, насколько сильно единицы в одной группе похожи друг на друга. Хотя это рассматривается как разновидность корреляция, в отличие от большинства других мер корреляции, он работает с данными, структурированными как группы, а не данными, структурированными как парные наблюдения.
В внутриклассовая корреляция обычно используется для количественной оценки степени, в которой люди с фиксированной степенью родства (например, полные братья и сестры) похожи друг на друга с точки зрения количественного признака (см. наследственность). Еще одно видное применение - это оценка согласованности или воспроизводимости количественных измерений, сделанных разными наблюдателями, измеряющими одно и то же количество.
Раннее определение ICC: беспристрастная, но сложная формула
Самая ранняя работа по внутриклассовой корреляции была сосредоточена на случае парных измерений, и первая предложенная статистика внутриклассовой корреляции (ICC) была модификацией модели межклассовая корреляция (Корреляции Пирсона).
Рассмотрим набор данных, состоящий из N парные значения данных (Иксп,1, Иксп,2), за п = 1, ..., N. Внутриклассовая корреляция р первоначально предложенный[2] к Рональд Фишер[3] является
куда
Более поздние версии этой статистики [3] использовал степени свободы 2N −1 в знаменателе для вычисления s2 и N −1 в знаменателе для вычисления р, так что s2 становится беспристрастным, и р становится беспристрастным, если s известен.
Ключевое различие между этим ICC и межклассовая корреляция (Пирсона) заключается в том, что данные объединяются для оценки среднего и дисперсии. Причина этого в том, что в настройках, где требуется внутриклассовая корреляция, пары считаются неупорядоченными. Например, если мы изучаем сходство близнецов, обычно нет значимого способа упорядочить значения для двух людей в паре близнецов. Как и межклассовая корреляция, внутриклассовая корреляция для парных данных будет ограничена интервал [−1, +1].
Внутриклассовая корреляция также определяется для наборов данных с группами, имеющими более 2 значений. Для групп, состоящих из трех значений, он определяется как[3]
куда
По мере роста количества элементов в группе растет и количество терминов, связанных с несколькими продуктами в этом выражении. Следующую эквивалентную форму вычислить проще:
куда K - количество значений данных в группе, и выборочное среднее пth группа.[3] Эту форму обычно относят к Харрис.[4] Левый член неотрицателен; следовательно, внутриклассовая корреляция должна удовлетворять
Для больших K, этот ICC почти равен
что можно интерпретировать как долю общей дисперсии, обусловленную вариациями между группами. Рональд Фишер посвящает целую главу внутриклассовой корреляции в своей классической книге Статистические методы для научных работников.[3]
Для данных от совокупности, которая полностью зашумлена, формула Фишера дает значения ICC, которые распределены около 0, то есть иногда являются отрицательными. Это связано с тем, что Фишер разработал формулу беспристрастной, и поэтому ее оценки иногда завышены, а иногда занижены. Для небольших или нулевых базовых значений в генеральной совокупности ICC, вычисленный по выборке, может быть отрицательным.
Современные определения ICC: более простая формула, но положительный уклон
Начиная с Рональда Фишера, внутриклассовая корреляция рассматривалась в рамках дисперсионный анализ (ANOVA), а в последнее время в рамках модели со случайными эффектами. Был предложен ряд оценок ICC. Большинство оценок можно определить в рамках модели случайных эффектов.
куда Yij это яth наблюдение в jth группа, μ в целом ненаблюдаемый иметь в виду, αj это ненаблюдаемый случайный эффект, присущий всем значениям в группе j, и εij это ненаблюдаемый шумовой термин.[5] Для идентификации модели αj и εij предполагается, что их ожидаемое значение равно нулю, и они не коррелируют друг с другом. Так же αj считаются одинаково распределенными, а εij предполагается, что они распределены одинаково. Дисперсия αj обозначается σ2
α и дисперсия εij обозначается σ2
ε.
ICC населения в этой структуре:[6]
Преимущество этой структуры ANOVA состоит в том, что разные группы могут иметь разное количество значений данных, что трудно обрабатывать, используя более раннюю статистику ICC. Этот ICC всегда неотрицателен, что позволяет интерпретировать его как долю общей дисперсии «между группами». Этот ICC можно обобщить, чтобы учесть ковариантные эффекты, и в этом случае ICC интерпретируется как фиксирование внутриклассового сходства значений данных, скорректированных по ковариате.[7]
Это выражение никогда не может быть отрицательным (в отличие от исходной формулы Фишера), и поэтому в выборках из популяции, у которой ICC равен 0, ICC в выборках будут выше, чем ICC популяции.
Было предложено несколько различных статистических данных ICC, не все из которых оценивают один и тот же параметр населения. Было много споров о том, какие статистические данные ICC подходят для конкретного использования, поскольку они могут давать заметно разные результаты для одних и тех же данных.[8][9]
Связь с коэффициентом корреляции Пирсона
В терминах своей алгебраической формы исходный ICC Фишера - это ICC, который больше всего напоминает Коэффициент корреляции Пирсона. Одно из ключевых различий между двумя статистическими данными заключается в том, что в ICC данные центрируются и масштабируются с использованием объединенного среднего и стандартного отклонения, тогда как в корреляции Пирсона каждая переменная центрируется и масштабируется с помощью своего собственного среднего и стандартного отклонения. Такое объединенное масштабирование для ICC имеет смысл, потому что все измерения имеют одинаковое количество (хотя и для единиц в разных группах). Например, в парном наборе данных, где каждая «пара» представляет собой одно измерение, сделанное для каждой из двух единиц (например, взвешивание каждого близнеца в паре однояйцевых близнецов), а не два разных измерения для одной единицы (например, измерение роста и вес для каждого человека), ICC - более естественная мера ассоциации, чем корреляция Пирсона.
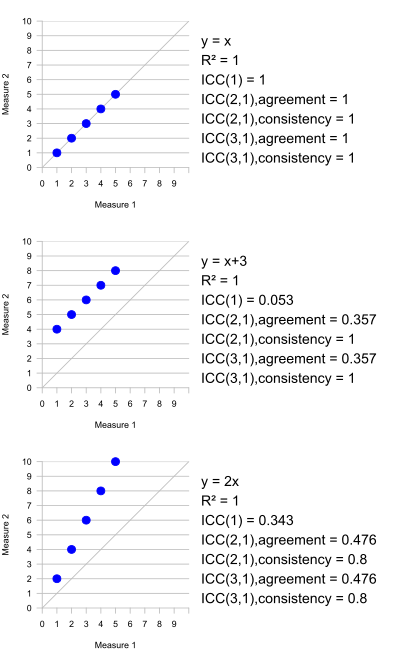
Важным свойством корреляции Пирсона является то, что она инвариантна к применению отдельных линейные преобразования к двум сравниваемым переменным. Таким образом, если мы коррелируем Икс и Y, где, скажем, Y = 2Икс +1, корреляция Пирсона между Икс и Y равно 1 - идеальное соотношение. Это свойство не имеет смысла для ICC, поскольку нет основы для решения, какое преобразование применяется к каждому значению в группе. Однако, если все данные во всех группах подвергаются одному и тому же линейному преобразованию, ICC не изменяется.
Использование при оценке соответствия среди наблюдателей
ICC используется для оценки согласованности или соответствия измерений, выполненных несколькими наблюдателями, измеряющими одну и ту же величину.[10] Например, если нескольких врачей попросят оценить результаты компьютерной томографии для выявления признаков прогрессирования рака, мы можем спросить, насколько согласованы эти оценки друг с другом. Если правда известна (например, если компьютерная томография была проведена у пациентов, которые впоследствии перенесли диагностическую операцию), то основное внимание, как правило, будет сосредоточено на том, насколько хорошо оценки врачей соответствуют истине. Если истина неизвестна, мы можем только рассмотреть сходство между оценками. Важным аспектом этой проблемы является то, что есть как наблюдатель и изменчивость внутри наблюдателя. Вариабельность между наблюдателями означает систематические различия между наблюдателями - например, один врач может постоянно оценивать пациентов с более высоким уровнем риска, чем другие врачи. Вариабельность внутри наблюдателя относится к отклонениям в оценке конкретного наблюдателя для конкретного пациента, которые не являются частью систематической разницы.
ICC предназначен для применения к обмениваемый измерения - то есть сгруппированные данные, в которых нет значимого способа упорядочить измерения внутри группы. При оценке соответствия между наблюдателями, если одни и те же наблюдатели оценивают каждый изучаемый элемент, то, вероятно, существуют систематические различия между наблюдателями, что противоречит понятию взаимозаменяемости. Если ICC используется в ситуации, когда существуют систематические различия, результатом является составная мера изменчивости внутри наблюдателя и между наблюдателями. Одна ситуация, при которой можно было бы разумно предположить, что имеет место возможность обмена, - это когда образец для оценки, скажем, образец крови, делится на несколько аликвот, и аликвоты измеряются отдельно на одном и том же приборе. В этом случае возможность замены будет сохраняться до тех пор, пока не будет никакого эффекта, связанного с последовательностью обработки образцов.
Поскольку коэффициент внутриклассовой корреляции дает смесь вариабельности внутри наблюдателя и между наблюдателями, его результаты иногда считаются трудными для интерпретации, когда наблюдатели не взаимозаменяемы. Альтернативные меры, такие как метод Коэна статистика каппа, то Флейсс каппа, а коэффициент корреляции согласованности[11] были предложены в качестве более подходящих мер согласия между невозмещаемыми наблюдателями.
Расчет в программных пакетах
ICC поддерживается в программном пакете с открытым исходным кодом р (используя функцию "icc" с пакетами пси или же irr, или через функцию «ICC» в пакете психопат.) rptR упаковка [12] предоставляет методы для оценки ICC и повторяемости для гауссовских, биномиальных и пуассоновских распределенных данных в рамках смешанной модели. Примечательно, что пакет позволяет оценивать скорректированный ICC (т. Е. Контролировать другие переменные) и вычислять доверительные интервалы на основе параметрической начальной загрузки и значения на основе перестановки остатков. Коммерческое программное обеспечение также поддерживает ICC, например Stata или же SPSS [13]
| Соглашение Shrout и Fleiss | Соглашение Макгроу и Вонга [14] | Имя в SPSS и Stata [15][16] |
|---|---|---|
| ICC (1,1) | Односторонний случайный, однократный ICC (1) | Односторонние случайные единичные меры |
| ICC (2,1) | Двусторонняя случайная, однократная оценка ICC (A, 1) | Двусторонняя случайная выборка, единичные измерения, абсолютное согласие |
| ICC (3,1) | Двусторонний смешанный, единый балл ICC (C, 1) | Двустороннее смешивание, отдельные меры, консистенция |
| неопределенный | Двусторонняя случайная, однократная оценка ICC (C, 1) | Двусторонняя случайная выборка, отдельные измерения, согласованность |
| неопределенный | Двусторонний смешанный, единый балл ICC (A, 1) | Двусторонний смешанный, единичные измерения, абсолютное согласие |
| ICC (1, k) | Односторонний случайный, средний балл ICC (k) | Односторонние случайные, средние меры |
| ICC (2, k) | Двусторонний случайный, средний балл ICC (A, k) | Двусторонние случайные, средние измерения, абсолютное согласие |
| ICC (3, k) | Двусторонний смешанный, средний балл ICC (C, k) | Двустороннее смешивание, средние размеры, консистенция |
| неопределенный | Двусторонний случайный, средний балл ICC (C, k) | Двусторонняя случайная выборка, средние измерения, согласованность |
| неопределенный | Двусторонний смешанный, средний балл ICC (A, k) | Двустороннее смешанное, средние измерения, абсолютное согласие |
Эти три модели:
- Односторонние случайные эффекты: каждый предмет оценивается различным набором из k случайно выбранных оценщиков;
- Двусторонняя случайность: случайным образом выбираются k оценщиков, затем каждый субъект оценивается одним и тем же набором k оценщиков;
- Двустороннее смешанное: определены k фиксированных рейтеров. Каждый предмет оценивается k оценщиками.
Количество измерений:
- Единичные меры: даже если в эксперименте проводится более одного измерения, надежность применяется к контексту, в котором будет выполнено одно измерение одного оценщика;
- Средние показатели: надежность применяется к контексту, в котором показатели k оценщиков будут усреднены по каждому предмету.
Последовательность или абсолютное согласие:
- Абсолютное согласие: представляет интерес согласие между двумя оценщиками, включая систематические ошибки обоих оценщиков и случайные остаточные ошибки;
- Согласованность: в контексте повторных измерений одним и тем же оценщиком систематические ошибки оценщика отменяются, и сохраняется только случайная остаточная ошибка.
Согласованность ICC не может быть оценена в модели односторонних случайных эффектов, так как нет способа разделить межэкспертную и остаточную дисперсии.
Интерпретация
Чиккетти (1994)[17] дает следующие часто цитируемые рекомендации по интерпретации каппа или меры по соглашению между экспертами ICC:
- Менее 0,40 - плохо.
- Между 0,40 и 0,59 - удовлетворительно.
- Между 0,60 и 0,74 - хорошо.
- От 0,75 до 1,00 - отлично.
Другое руководство дано Ку и Ли (2016):[18]
- ниже 0,50: плохо
- от 0,50 до 0,75: умеренный
- от 0,75 до 0,90: хорошо
- выше 0,90: отлично
Смотрите также
Рекомендации
- ^ Кох, Гэри Г. (1982). «Коэффициент внутриклассовой корреляции». В Сэмюэле Коце и Нормане Л. Джонсоне (ред.). Энциклопедия статистических наук. 4. Нью-Йорк: Джон Уайли и сыновья. С. 213–217.
- ^ Бартко Ю.Ю. (август 1966 г.). «Коэффициент внутриклассовой корреляции как показатель надежности». Психологические отчеты. 19 (1): 3–11. Дои:10.2466 / пр0.1966.19.1.3. PMID 5942109.
- ^ а б c d е Рональд А. Фишер (1954). Статистические методы для научных работников (Двенадцатое изд.). Эдинбург: Оливер и Бойд. ISBN 978-0-05-002170-5.
- ^ Дж. Артур Харрис (Октябрь 1913 г.). «О вычислении внутриклассовых и межклассовых коэффициентов корреляции по классовым моментам при большом количестве возможных комбинаций». Биометрика. 9 (3/4): 446–472. Дои:10.1093 / biomet / 9.3-4.446. JSTOR 2331901.
- ^ Доннер А., Коваль Дж. Дж. (Март 1980 г.). «Оценка внутриклассовой корреляции при анализе семейных данных». Биометрия. 36 (1): 19–25. Дои:10.2307/2530491. JSTOR 2530491. PMID 7370372.
- ^ Доказательство того, что ICC в модели Anova является корреляцией двух элементов: ocram[1], Понимание коэффициента внутриклассовой корреляции, URL (версия: 2012-12-05): [2]
- ^ Станиш, Уильям; Тейлор, Ноэль (1983). «Оценка коэффициента внутриклассовой корреляции для анализа модели ковариации». Американский статистик. 37 (3): 221–224. Дои:10.2307/2683375. JSTOR 2683375.
- ^ Мюллер Р., Бюттнер П. (декабрь 1994 г.). «Критическое обсуждение коэффициентов внутриклассовой корреляции». Статистика в медицине. 13 (23–24): 2465–76. Дои:10.1002 / sim.4780132310. PMID 7701147. См. Также комментарий:
- П. Варга (1997). "Письмо редактору". Статистика в медицине. 16 (7): 821–823. Дои:10.1002 / (SICI) 1097-0258 (19970415) 16: 7 <821 :: AID-SIM558> 3.0.CO; 2-B.
- ^ Кеннет О. МакГроу и С. П. Вонг (1996). «Формирование выводов о некоторых коэффициентах внутриклассовой корреляции». Психологические методы. 1: 30–46. Дои:10.1037 / 1082-989X.1.1.30. В статье есть несколько ошибок:
- Кеннет О. Макгроу и С. П. Вонг (1996). «Поправка к Макгроу и Вонгу (1996)». Психологические методы. 1 (4): 390. Дои:10.1037 / 1082-989x.1.4.390.
- ^ Shrout PE, Fleiss JL (март 1979 г.). «Внутриклассовые корреляции: использование при оценке надежности оценщика». Психологический бюллетень. 86 (2): 420–8. Дои:10.1037/0033-2909.86.2.420. PMID 18839484.
- ^ Кэрол А. Э. Никерсон (декабрь 1997 г.). "Примечание о коэффициенте корреляции согласованности для оценки воспроизводимости"'". Биометрия. 53 (4): 1503–1507. Дои:10.2307/2533516. JSTOR 2533516.
- ^ Стоффель М.А., Накагава С., Шильцет Х. (2017). «rptR: оценка повторяемости и разложение дисперсии с помощью обобщенных линейных моделей со смешанными эффектами». Методы в экологии и эволюции. 8 (11): 1639–1644. Дои:10.1111 / 2041-210x.12797. ISSN 2041–210X.
- ^ Ричард Н. Макленнан (ноябрь 1993 г.). «Надежность Interrater с SPSS для Windows 5.0». Американский статистик. 47 (4): 292–296. Дои:10.2307/2685289. JSTOR 2685289.
- ^ Кеннет О. Макгроу; С. П. Вонг (1996). «Формирование выводов о некоторых коэффициентах внутриклассовой корреляции». Психологические методы. 1 (1): 30–40. Дои:10.1037 / 1082-989X.1.1.30.
- ^ Руководство пользователя Stata выпуск 15 (PDF). Колледж-Стейшн, Техас: Stata Press. 2017. С. 1101–1123. ISBN 978-1-59718-249-2.
- ^ Дэвид К. Хауэлл. «Коэффициенты внутриклассовой корреляции» (PDF).
- ^ Чиккетти, Доменик В. (1994). «Руководящие принципы, критерии и практические правила для оценки нормированных и стандартизированных инструментов оценки в психологии». Психологическая оценка. 6 (4): 284–290. Дои:10.1037/1040-3590.6.4.284.
- ^ Ку Т.К., Ли М.Й. (июнь 2016 г.). «Руководство по выбору и представлению коэффициентов внутриклассовой корреляции для исследования надежности». Журнал хиропрактики. 15 (2): 155–63. Дои:10.1016 / j.jcm.2016.02.012. ЧВК 4913118. PMID 27330520.