WikiDer > Выборка с обратным преобразованием

Выборка с обратным преобразованием (также известен как инверсионная выборка, то обратное интегральное преобразование вероятности, то метод обратного преобразования, Смирнов преобразовать, или Золотое правило^[1]) является основным методом выборка псевдослучайных чисел, т.е. для генерации номеров выборок при случайный из любого распределение вероятностей учитывая его кумулятивная функция распределения.

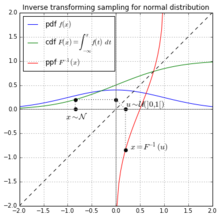
Выборка с обратным преобразованием занимает однородные образцы из числа ${ displaystyle u}$ от 0 до 1, интерпретируется как вероятность, а затем возвращает наибольшее число ${ displaystyle x}$ из области распространения ${ Displaystyle P (X)}$ такой, что ${ Displaystyle P (- infty$. Например, представьте, что ${ Displaystyle P (X)}$ это стандарт нормальное распределение с нулевым средним и единичным стандартным отклонением. В таблице ниже показаны образцы, взятые из равномерного распределения, и их представление в стандартном нормальном распределении.

Преобразование однородного образца в нормальный

${ displaystyle u}$	${ Displaystyle F ^ {- 1} (и)}$
.5	0
.975	1.95996
.995	2.5758
.999999	4.75342
1-2^{-52}	8.12589

Выборка с обратным преобразованием для нормального распределения

Мы случайным образом выбираем долю площади под кривой и возвращаем число в домене так, чтобы именно эта доля площади находилась слева от этого числа. Интуитивно кажется, что мы вряд ли выберем число на дальнем конце хвостов, потому что в них очень мало области, что потребовало бы выбора числа, очень близкого к нулю или единице.

С вычислительной точки зрения этот метод включает вычисление квантильная функция распределения - другими словами, вычисление кумулятивная функция распределения (CDF) распределения (который отображает число в домене с вероятностью от 0 до 1), а затем инвертирует эту функцию. Отсюда термин «инверсия» или «инверсия» в большинстве названий этого метода. Обратите внимание, что для дискретное распределение, вычисление CDF в общем случае не слишком сложно: мы просто складываем индивидуальные вероятности для различных точек распределения. Для непрерывное распространение, однако нам нужно интегрировать функция плотности вероятности (PDF) распределения, что невозможно сделать аналитически для большинства распределений (включая нормальное распределение). В результате этот метод может быть неэффективным с вычислительной точки зрения для многих дистрибутивов, поэтому предпочтение отдается другим методам; тем не менее, это полезный метод для создания более общих пробоотборников, например, основанных на отбраковка.

Для нормальное распределение, отсутствие аналитического выражения для соответствующей функции квантили означает, что другие методы (например, Преобразование Бокса – Мюллера) может быть предпочтительнее с вычислительной точки зрения. Часто бывает так, что даже для простых распределений метод выборки с обратным преобразованием может быть улучшен на:^[2] см., например, алгоритм зиккурата и отбраковка. С другой стороны, можно очень точно аппроксимировать функцию квантиля нормального распределения, используя полиномы умеренной степени, и на самом деле метод этого достаточно быстр, так что инверсионная выборка теперь является методом по умолчанию для выборки из нормального распределения. в статистическом пакете р.^[3]

Определение

В интегральное преобразование вероятности заявляет, что если ${ displaystyle X}$ это непрерывная случайная величина с участием кумулятивная функция распределения ${ displaystyle F_ {X}}$, то случайная величина ${ Displaystyle Y = F_ {X} (X)}$ имеет равномерное распределение на [0, 1]. Обратное интегральное преобразование вероятности - это как раз обратное этому: в частности, если ${ displaystyle Y}$ имеет равномерное распределение на [0, 1] и если ${ displaystyle X}$ имеет кумулятивное распределение ${ displaystyle F_ {X}}$, то случайная величина ${ Displaystyle F_ {X} ^ {- 1} (Y)}$ имеет то же распределение, что и ${ displaystyle X}$ .

График техники инверсии от ${ displaystyle x}$ к ${ Displaystyle F (х)}$. Справа внизу мы видим обычную функцию, а слева вверху - ее инверсию.

Интуиции

От ${ Displaystyle U sim mathrm {Unif} [0,1]}$, мы хотим сгенерировать ${ displaystyle X}$ с участием CDF ${ displaystyle F_ {X} (x).}$ Мы предполагаем ${ Displaystyle F_ {X} (х)}$ быть строго возрастающей функцией, что обеспечивает хорошую интуицию.

Мы хотим увидеть, сможем ли мы найти строго монотонное преобразование ${ Displaystyle Т: [0,1] mapsto mathbb {R}}$, так что ${ Displaystyle Т (U) { overset {d} {=}} X}$. У нас будет

${ Displaystyle F_ {X} (х) = Pr (X leq x) = Pr (T (U) leq x) = Pr (U Leq T ^ {- 1} (x)) = T ^ {- 1} (x), { text {for}} x in mathbb {R},}$

где последний шаг использовал это ${ Displaystyle Pr (U Leq y) = y}$ когда ${ displaystyle U}$ единообразно на ${ displaystyle (0,1)}$.

Итак, мы получили ${ displaystyle F_ {X}}$ быть обратной функцией ${ displaystyle T}$, или, что эквивалентно ${ displaystyle T (u) = F_ {X} ^ {- 1} (u), u in [0,1].}$

Следовательно, мы можем сгенерировать ${ displaystyle X}$ от ${ displaystyle F_ {X} ^ {- 1} (U).}$

Метод

Схема обратного преобразования выборки. Обратная функция ${ Displaystyle у = F_ {X} (х)}$ можно определить как ${ Displaystyle F_ {X} ^ {- 1} (y) = mathrm {inf} {x | F_ {X} (x) geq y }}$.

Проблема, которую решает метод выборки с обратным преобразованием, заключается в следующем:

• Позволять ${ displaystyle X}$ быть случайная переменная распределение которого можно описать кумулятивная функция распределения ${ displaystyle F_ {X}}$.
• Мы хотим генерировать значения ${ displaystyle X}$ которые распределяются согласно этому распределению.

Метод выборки обратного преобразования работает следующим образом:

1. Сгенерировать случайное число ${ displaystyle u}$ из стандартного равномерного распределения в интервале ${ displaystyle [0,1]}$, например от ${ Displaystyle U sim mathrm {Unif} [0,1].}$
2. Найдите обратную величину желаемой функции CDF, например ${ Displaystyle F_ {X} ^ {- 1} (х)}$.
3. Вычислить ${ Displaystyle X = F_ {X} ^ {- 1} (u)}$. Вычисляемая случайная величина ${ displaystyle X}$ имеет распространение ${ Displaystyle F_ {X} (х)}$.

Выражаясь иначе, учитывая непрерывную однородную переменную ${ displaystyle U}$ в ${ displaystyle [0,1]}$ и обратимый кумулятивная функция распределения ${ displaystyle F_ {X}}$, случайная величина ${ Displaystyle X = F_ {X} ^ {- 1} (U)}$ имеет распространение ${ displaystyle F_ {X}}$ (или, ${ displaystyle X}$ распространяется ${ displaystyle F_ {X}}$).

Может быть дана трактовка таких обратных функций как объектов, удовлетворяющих дифференциальным уравнениям.^[4] Некоторые такие дифференциальные уравнения допускают явные решения в виде степенных рядов, несмотря на их нелинейность.^{[нужна цитата]}

Примеры

• В качестве примера предположим, что у нас есть случайная величина ${ Displaystyle U sim mathrm {Unif} (0,1)}$ и кумулятивная функция распределения

${ displaystyle { begin {align} F (x) = 1- exp (- { sqrt {x}}) end {align}}}$

Чтобы выполнить инверсию, мы хотим решить для ${ Displaystyle F (F ^ {- 1} (u)) = u}$

${ Displaystyle { begin {align} F (F ^ {- 1} (u)) & = u 1- exp left (- { sqrt {F ^ {- 1} (u)}} справа) & = u F ^ {- 1} (u) & = (- log (1-u)) ^ {2} & = ( log (1-u)) ^ {2} конец {выровнен}}}$

Отсюда мы будем выполнять шаги один, два и три.

• В качестве другого примера мы используем экспоненциальное распределение с участием ${ Displaystyle F_ {X} (х) = 1-е ^ {- лямбда х}}$ для x ≥ 0 (и 0 в противном случае). Решая y = F (x), получаем обратную функцию

${ displaystyle x = F ^ {- 1} (y) = - { frac {1} { lambda}} ln (1-y).}$

Это означает, что если мы нарисуем ${ displaystyle y_ {0}}$из ${ Displaystyle U sim mathrm {Unif} (0,1)}$ и вычислить ${ displaystyle x_ {0} = F_ {X} ^ {- 1} (y_ {0}) = - { frac {1} { lambda}} ln (1-y_ {0}),}$ Эта ${ displaystyle x_ {0}}$ имеет экспоненциальное распределение.

Идея проиллюстрирована на следующем графике:

Случайные числа y_я генерируются из равномерного распределения между 0 и 1, то есть Y ~ U (0, 1). Они отображаются в виде цветных точек на оси Y. Каждая из точек отображается в соответствии с x = F⁻¹(y), который показан серыми стрелками для двух примерных точек. В этом примере мы использовали экспоненциальное распределение. Следовательно, при x ≥ 0 плотность вероятности равна ${ displaystyle varrho _ {X} (x) = lambda e ^ {- lambda , x}}$ а кумулятивная функция распределения равна ${ Displaystyle F (х) = 1-е ^ {- лямбда , х}}$. Следовательно, ${ displaystyle x = F ^ {- 1} (y) = - { frac { ln (1-y)} { lambda}}}$. Мы можем видеть, что при использовании этого метода многие точки в конечном итоге близки к нулю, и только несколько точек в конечном итоге имеют высокие значения x - так же, как и ожидается для экспоненциального распределения.

Обратите внимание, что распределение не изменится, если мы начнем с 1-y вместо y. Поэтому для вычислительных целей достаточно сгенерировать случайные числа y в [0, 1], а затем просто вычислить

${ displaystyle x = F ^ {- 1} (y) = - { frac {1} { lambda}} ln (y).}$

Доказательство правильности

Позволять F быть непрерывным кумулятивная функция распределения, и разреши F⁻¹ быть его обратной функцией (используя инфимум поскольку CDF слабо монотонны и непрерывный вправо):^[5]

${ Displaystyle F ^ {- 1} (u) = inf ; {x mid F (x) geq u } qquad (0$

Запрос: Если U это униформа случайная величина на (0, 1), тогда ${ Displaystyle F ^ {- 1} (U)}$ имеет F как его CDF.

Доказательство:

${ Displaystyle { begin {align} & Pr (F ^ {- 1} (U) leq x) & {} = Pr (U leq F (x)) quad & ({ text {применяя}} F, { text {к обеим сторонам}}) & {} = F (x) quad & ({ text {потому что}} Pr (U leq y) = y, { текст {когда U единообразно на}} (0,1)) конец {выровнено}}}$

Усеченное распределение