WikiDer > Розетка Клемперера
А Розетка Клемперер это гравитационный система более тяжелых и легких тел, вращающихся по регулярному повторяющемуся узору вокруг общей барицентр. Впервые он был описан В. Б. Клемперер в 1962 г.,[1] и является частным случаем центральная конфигурация.
Клемперер описал систему следующим образом:
Такой симметрией также обладает своеобразное семейство геометрических конфигураций, которые можно описать как «розетки». В них четное количество «планет» двух (или более) видов, одна (или несколько) тяжелее другой, но все они имеют равную массу, размещены по углам двух (или более) пересекающихся правильных многоугольников. так что более легкие и тяжелые чередуются (или следуют друг за другом циклически).
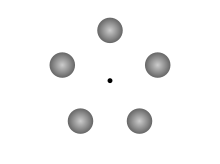
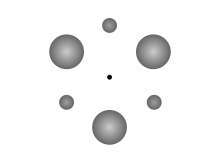
Простейшая розетка будет состоять из четырех чередующихся более тяжелых и более легких тел, расположенных под углом 90 градусов друг от друга, в ромбический конфигурация [Heavy, Light, Heavy, Light], где два больших тела имеют одинаковую массу, а также два меньших тела имеют одинаковую массу. Количество «массовых типов» может быть увеличено до тех пор, пока шаблон расположения является циклическим: например, [1,2,3 ... 1,2,3], [1,2,3,4,5 ... 1,2,3,4,5], [1,2,3,3,2 , 1 ... 1,2,3,3,2,1] и т. Д.
Клемперер также упомянул восьмиугольный и ромбический розетки. В то время как все розетки Клемперера уязвимы для дестабилизации, шестиугольная розетка имеет дополнительную стабильность, потому что «планеты» находятся в L4 и L5 друг друга. Лагранжевые точки.
Неправильное использование и орфографические ошибки
Термин «розетка Клемперера» (часто написанная с ошибками)Кемплерер розетка ") часто используется для обозначения конфигурации из трех или более равных масс, установленных в точках равносторонний многоугольник и учитывая равный угловая скорость о них центр массы. Клемперер действительно упоминает эту конфигурацию в начале своей статьи, но только как уже известный набор равновесных систем перед тем, как представить фактические розетки.
В Ларри Нивенроман Кольцо, то Кукловоды "Флот Миров"устроен в такой конфигурации (5 планет, расположенных в точках пятиугольник), которую Нивен называет «розеткой Кемплера»; эта (возможно, преднамеренная) орфография (и неправильное использование) является одним из возможных источников путаницы. Примечательно, что эти вымышленные планеты удерживались на месте большими двигателями в дополнение к гравитационной силе. Другой пример - сходство между именем Клемперера и именем Иоганн Кеплер, который описал некоторые законы движения планет в 17 веке.
Нестабильность
Моделирование этой системы[2] (или простой линейный анализ возмущений) демонстрируют, что такие системы нестабильны: любое движение в сторону от идеальной геометрической конфигурации вызывает колебания, в конечном итоге приводящие к разрушению системы (исходная статья Клемперера также утверждает этот факт). Это справедливо независимо от того, находится ли центр розетки в свободном пространстве или на орбите вокруг звезды. Краткая причина состоит в том, что любое возмущение разрушает симметрию, что увеличивает возмущение, что еще больше нарушает симметрию и так далее.
Более подробное объяснение состоит в том, что любое тангенциальное возмущение приближает тело к одному соседу и дальше от другого; гравитационный дисбаланс становится больше по направлению к более близкому соседу и меньше по направлению к более дальнему соседу, притягивая возмущенный объект дальше к его более близкому соседу, усиливая возмущение, а не демпфируя его. Радиальное возмущение внутрь заставляет возмущенное тело приближаться к все другие объекты, увеличивая силу, действующую на объект, и увеличивая его орбитальную скорость, что косвенно приводит к тангенциальному возмущению и приведенному выше аргументу.
Рекомендации
- ^ Клемперер, В. Б. (апрель 1962 г.). «Некоторые свойства розеточных конфигураций гравитирующих тел в гомографическом равновесии». Астрономический журнал. 67 (3): 162–167. Bibcode:1962AJ ..... 67..162K. Дои:10.1086/108686.
- ^ Дженкинс, Боб. "Розетки Клемперера". Получено 2007-01-12.