В физика конденсированного состояния , то Волновая функция Лафлина [1] [2] анзац , предложено Роберт Лафлин для основное состояние из двумерный электронный газ размещены на едином фоне магнитное поле при наличии униформы желе фон, когда коэффициент заполнения (квантовый эффект Холла) из самый низкий уровень Ландау является ν = 1 / п { displaystyle nu = 1 / n} п { displaystyle n} ν = 1 / 3 { displaystyle nu = 1/3} дробный квантовый эффект Холла , и предсказал существование дополнительных ν = 1 / п { displaystyle nu = 1 / n} е / п { displaystyle e / n} Нобелевская премия по физике в 1998 г. за это открытие. Будучи пробной волновой функцией, она не точна, но качественно воспроизводит многие особенности точного решения и количественно имеет очень высокие перекрытия с точным основным состоянием для небольших систем.
Если не обращать внимания на желе и взаимное Кулоновское отталкивание Между электронами в качестве нулевого приближения у нас есть бесконечно вырожденный нижний уровень Ландау (НУЛ), и с коэффициентом заполнения 1 / п можно ожидать, что все электроны будут находиться в НУЛ. Включив взаимодействия, мы можем сделать приближение, что все электроны лежат в НУЛ. Если ψ 0 { displaystyle psi _ {0}} орбитальный угловой момент , то анзац Лафлина для многочастичной волновой функции имеет вид
⟨ z 1 , z 2 , z 3 , … , z N ∣ п , N ⟩ = ψ п , N ( z 1 , z 2 , z 3 , … , z N ) = D [ ∏ N ⩾ я > j ⩾ 1 ( z я − z j ) п ] ∏ k = 1 N exp ( − ∣ z k ∣ 2 ) { displaystyle langle z_ {1}, z_ {2}, z_ {3}, ldots, z_ {N} mid n, N rangle = psi _ {n, N} (z_ {1}, z_ {2}, z_ {3}, ldots, z_ {N}) = D left [ prod _ {N geqslant i> j geqslant 1} left (z_ {i} -z_ {j} right ) ^ {n} right] prod _ {k = 1} ^ {N} exp left (- mid z_ {k} mid ^ {2} right)} где позиция обозначается
z = 1 2 л B ( Икс + я у ) { Displaystyle Z = {1 более 2 { mathit {l}} _ {B}} left (x + iy right)} в (Гауссовы единицы )
л B = ℏ c е B { displaystyle { mathit {l}} _ {B} = { sqrt { hbar c over eB}}} и Икс { displaystyle x} у { displaystyle y} ℏ { displaystyle hbar} Постоянная Планка , е { displaystyle e} заряд электрона , N { displaystyle N} B { displaystyle B} магнитное поле , которая перпендикулярна плоскости xy. Индексы на z обозначают частицу. Чтобы волновая функция описывала фермионы , n должно быть нечетным целым числом. Это заставляет волновую функцию быть антисимметричной по отношению к обмену частицами. Угловой момент для этого состояния равен п ℏ { displaystyle n hbar}
Энергия взаимодействия двух частиц
Рисунок 1. Энергия взаимодействия в зависимости от
л { displaystyle { mathit {l}}} за
п = 7 { displaystyle n = 7} и
k B р B = 20 { displaystyle k_ {B} r_ {B} = 20} . Энергия выражается в единицах
е 2 L B { Displaystyle {е ^ {2} над L_ {B}}} . Обратите внимание, что минимумы возникают при
л = 3 { displaystyle { mathit {l}} = 3} и
л = 4 { displaystyle { mathit {l}} = 4} . Обычно минимумы возникают при
л п = 1 2 ± 1 2 п { displaystyle {{ mathit {l}} over n} = {1 over 2} pm {1 over 2n}} .
Волновая функция Лафлина - это многочастичная волновая функция для квазичастицы . В ожидаемое значение энергии взаимодействия пары квазичастиц равна
⟨ V ⟩ = ⟨ п , N ∣ V ∣ п , N ⟩ , N = 2 { Displaystyle langle V rangle = langle n, N mid V mid n, N rangle, ; ; ; N = 2} где экранированный потенциал (см. Кулоновский потенциал между двумя токовыми петлями, заключенными в магнитное поле )
V ( р 12 ) = ( 2 е 2 L B ) ∫ 0 ∞ k d k k 2 + k B 2 р B 2 M ( л + 1 , 1 , − k 2 4 ) M ( л ′ + 1 , 1 , − k 2 4 ) J 0 ( k р 12 р B ) { displaystyle V left (r_ {12} right) = left ({2e ^ {2} over L_ {B}} right) int _ {0} ^ { infty} {{k ; dk ;} над k ^ {2} + k_ {B} ^ {2} r_ {B} ^ {2}} ; M left ({ mathit {l}} + 1,1, - {k ^ {2} over 4} right) ; M left ({ mathit {l}} ^ { prime} +1,1, - {k ^ {2} over 4} right) ; { mathcal {J}} _ {0} left (k {r_ {12} over r_ {B}} right)} куда M { displaystyle M} конфлюэнтная гипергеометрическая функция и J 0 { displaystyle { mathcal {J}} _ {0}} Функция Бесселя первого вида. Здесь, р 12 { displaystyle r_ {12}} е { displaystyle e} заряд электрона , р B = 2 л B { displaystyle r_ {B} = { sqrt {2}} { mathit {l}} _ {B}} Ларморовский радиус , и L B { displaystyle L_ {B}} угловые моменты двух отдельных токовых петель л ℏ { Displaystyle { mathit {l}} hbar} л ′ ℏ { Displaystyle { mathit {l}} ^ { prime} hbar} л + л ′ = п { Displaystyle { mathit {l}} + { mathit {l}} ^ { prime} = п} Гауссовы единицы )
k B 2 = 4 π е 2 ℏ ω c А L B { displaystyle k_ {B} ^ {2} = {4 pi e ^ {2} over hbar omega _ {c} AL_ {B}}} куда ω c { displaystyle omega _ {c}} циклотронная частота , и А { displaystyle A}
Энергия взаимодействия оценивается как:
E = ( 2 е 2 L B ) ∫ 0 ∞ k d k k 2 + k B 2 р B 2 M ( л + 1 , 1 , − k 2 4 ) M ( л ′ + 1 , 1 , − k 2 4 ) M ( п + 1 , 1 , − k 2 2 ) { displaystyle E = left ({2e ^ {2} over L_ {B}} right) int _ {0} ^ { infty} {{k ; dk ;} over k ^ {2 } + k_ {B} ^ {2} r_ {B} ^ {2}} ; M left ({ mathit {l}} + 1,1, - {k ^ {2} over 4} right ) ; M left ({ mathit {l}} ^ { prime} +1,1, - {k ^ {2} over 4} right) ; M left (n + 1,1, - {k ^ {2} over 2} right)}
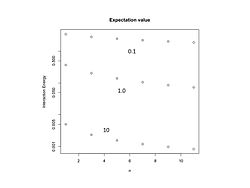
Рисунок 2. Энергия взаимодействия в зависимости от
п { displaystyle {n}} за
л п = 1 2 ± 1 2 п { displaystyle {{ mathit {l}} over n} = {1 over 2} pm {1 over 2n}} и
k B р B = 0.1 , 1.0 , 10 { displaystyle k_ {B} r_ {B} = 0,1,1,0,10} . Энергия выражается в единицах
е 2 L B { Displaystyle {е ^ {2} над L_ {B}}} .
Чтобы получить этот результат, мы сделали замену переменных интегрирования
ты 12 = z 1 − z 2 2 { displaystyle u_ {12} = {z_ {1} -z_ {2} over { sqrt {2}}}} и
v 12 = z 1 + z 2 2 { displaystyle v_ {12} = {z_ {1} + z_ {2} over { sqrt {2}}}} и отметил (см. Общие интегралы в квантовой теории поля )
1 ( 2 π ) 2 2 2 п п ! ∫ d 2 z 1 d 2 z 2 ∣ z 1 − z 2 ∣ 2 п exp [ − 2 ( ∣ z 1 ∣ 2 + ∣ z 2 ∣ 2 ) ] J 0 ( 2 k ∣ z 1 − z 2 ∣ ) = { displaystyle {1 over left (2 pi right) ^ {2} ; 2 ^ {2n} ; n!} int d ^ {2} z_ {1} ; d ^ {2} z_ {2} ; mid z_ {1} -z_ {2} mid ^ {2n} ; exp left [-2 left ( mid z_ {1} mid ^ {2} + mid z_ {2} mid ^ {2} right) right] ; { mathcal {J}} _ {0} left ({ sqrt {2}} ; {k mid z_ {1} - z_ {2} mid} right) =} 1 ( 2 π ) 2 2 п п ! ∫ d 2 ты 12 d 2 v 12 ∣ ты 12 ∣ 2 п exp [ − 2 ( ∣ ты 12 ∣ 2 + ∣ v 12 ∣ 2 ) ] J 0 ( 2 k ∣ ты 12 ∣ ) = { displaystyle {1 over left (2 pi right) ^ {2} ; 2 ^ {n} ; n!} int d ^ {2} u_ {12} ; d ^ {2} v_ {12} ; mid u_ {12} mid ^ {2n} ; exp left [-2 left ( mid u_ {12} mid ^ {2} + mid v_ {12} mid ^ {2} right) right] ; { mathcal {J}} _ {0} left ({2} k mid u_ {12} mid right) =} M ( п + 1 , 1 , − k 2 2 ) . { displaystyle M left (n + 1,1, - {k ^ {2} over 2} right).} Энергия взаимодействия имеет минимумы при (рис. 1)
л п = 1 3 , 2 5 , 3 7 , так далее., { displaystyle {{ mathit {l}} over n} = {1 over 3}, {2 over 5}, {3 over 7}, { mbox {и т. д.,}}} и
л п = 2 3 , 3 5 , 4 7 , и Т. Д. { displaystyle {{ mathit {l}} over n} = {2 over 3}, {3 over 5}, {4 over 7}, { mbox {и т. д.}}} Для этих значений отношения угловых моментов энергия представлена на рисунке 2 как функция от п { displaystyle n}
Рекомендации
^ Лафлин, Р. Б. (2 мая 1983 г.). «Аномальный квантовый эффект Холла: несжимаемая квантовая жидкость с фракционно заряженными возбуждениями». Письма с физическими проверками . Американское физическое общество (APS). 50 (18): 1395–1398. Дои :10.1103 / Physrevlett.50.1395 . ISSN 0031-9007 . ^ З. Ф. Эзева (2008). Квантовые эффекты Холла, второе издание . World Scientific. ISBN 978-981-270-032-2 Смотрите также





![langle z_1, z_2, z_3, ldots, z_N mid n, N rangle
знак равно
psi_ {n, N} (z_1, z_2, z_3, ldots, z_N)
знак равно
D left [ prod_ {N geqslant i> j geqslant 1} left (z_i-z_j right) ^ n right] prod ^ N_ {k = 1} exp left (- mid z_k середина ^ 2 справа)](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2500bd725cdb2da0c016b6be9e3ffebe1b5790f)



































![{1 над влево (2 пи вправо) ^ 2 ; 2 ^ {2n} ; п! }
int d ^ 2z_1 ; d ^ 2z_2 ; mid z_1 - z_2 mid ^ {2n} ; exp left [- 2 left ( mid z_1 mid ^ 2 + mid z_2 mid ^ 2 right) right] ; mathcal J_0 left ( sqrt {2} ; {k mid z_1 - z_2 mid} right)
знак равно](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c2d3b7f868aba752a4ef9c00749b9bf7bfc5511)
![{1 над влево (2 пи вправо) ^ 2 ; 2 ^ {n} ; п! }
int d ^ 2u_ {12} ; d ^ 2v_ {12} ; mid u_ {12} mid ^ {2n} ; exp left [- 2 left ( mid u_ {12} mid ^ 2 + mid v_ {12} mid ^ 2 right) right] ; mathcal J_0 left ({2} k mid u_ {12} mid right)
знак равно](https://wikimedia.org/api/rest_v1/media/math/render/svg/b96ab64f1028a97d4c44a6ea8592a52198bb1f47)


