WikiDer > Магнитосопротивление

Magnetoresistance

Магнитосопротивление тенденция материала (часто ферромагнетика) изменять электрическое сопротивление во внешнем магнитное поле. Есть множество эффектов, которые можно назвать магнитосопротивлением. Некоторые из них встречаются в объемных немагнитных металлах и полупроводниках, например, геометрическое магнитосопротивление, Осцилляции Шубникова – де Гааза., или обычное положительное магнитосопротивление в металлах.^[1] Другие эффекты возникают в магнитных металлах, например, отрицательное магнитосопротивление в ферромагнетиках.^[2] или анизотропное магнитосопротивление (AMR). Наконец, в многокомпонентных или многослойных системах (например, магнитных туннельных переходах), гигантское магнитосопротивление (GMR), туннельное магнитосопротивление (ПМР), колоссальное магнитосопротивление (CMR) и необычайное магнитосопротивление (ЭМИ) можно наблюдать.

Первый магниторезистивный эффект был открыт в 1856 г. Уильям Томсон, более известный как лорд Кельвин, но он не смог снизить электрическое сопротивление чего-либо более чем на 5%. Сегодня системы, в том числе полуметаллы^[3] и концентрическое кольцо EMR структуры известны. В них магнитное поле может регулировать сопротивление на порядки величины. Поскольку различные механизмы могут изменять сопротивление, полезно отдельно рассматривать ситуации, когда оно напрямую зависит от магнитного поля (например, геометрическое магнитосопротивление и многополосное магнитосопротивление), и те, где это происходит косвенно, через намагничивание (например, AMR и TMR).

Открытие

Уильям Томсон (лорд Кельвин) впервые открыл обычное магнитосопротивление в 1856 году.^[4] Он экспериментировал с кусками железа и обнаружил, что сопротивление увеличивается, когда ток идет в том же направлении, что и магнитная сила, и уменьшается, когда ток находится под углом 90 ° к магнитной силе. Затем он проделал тот же эксперимент с никелем и обнаружил, что на него влияет то же самое, но величина эффекта была больше. Этот эффект называется анизотропным магнитосопротивлением (АМС).

Воспроизвести медиа

Анимация об открытии магнитосопротивления Графики

Диск Корбино. Когда магнитное поле выключено, в проводящем кольцевом пространстве течет радиальный ток из-за батареи, подключенной между (бесконечными) ободами проводимости. Когда магнитное поле вдоль оси включено, (B указывает прямо из страницы) Сила Лоренца возбуждает круговую составляющую тока, и сопротивление между внутренним и внешним ободами возрастает. Это увеличение сопротивления из-за магнитного поля называется магнитосопротивление.

В 2007, Альберт Ферт и Петер Грюнберг были совместно удостоены Нобелевской премии за открытие Гигантское магнитосопротивление.^[5]

Геометрическое магнитосопротивление

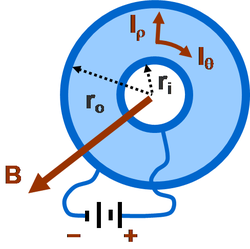
Пример магнитосопротивления за счет прямого воздействия магнитного поля на электрический ток можно изучить на диске Корбино (см. Рисунок), который представляет собой проводящее кольцо с идеально проводящими ободами. Без магнитного поля аккумулятор запускает радиальный ток между ободами. При приложении магнитного поля, перпендикулярного плоскости кольцевого пространства (внутрь или за пределы страницы), также течет круговая составляющая тока из-за Сила Лоренца. Первоначальный интерес к этой проблеме возник у Больцмана в 1886 году и независимо был повторно исследован Корбино в 1911 году.^[6]

В простой модели, если предположить, что реакция на силу Лоренца такая же, как для электрического поля, скорость носителя v дан кем-то:

{ Displaystyle mathbf {v} = mu left ( mathbf {E} + mathbf {v times B} right), }

где μ - подвижность носителей. Решая для скорости, находим:

{ displaystyle mathbf {v} = { frac { mu} {1 + ( mu B) ^ {2}}} left ( mathbf {E} + mu mathbf {E times B} + mu ^ {2} ( mathbf {B cdot E}) mathbf {B} right) = { frac { mu} {1 + ( mu B) ^ {2}}} left ( mathbf {E} _ { perp} + mu mathbf {E times B} right) + mu mathbf {E} _ { parallel}, }

где эффективное снижение мобильности из-за B-поле (для движения перпендикулярно этому полю) очевидно. Электрический ток (пропорциональный радиальной составляющей скорости) будет уменьшаться с увеличением магнитного поля и, следовательно, сопротивление устройства будет увеличиваться. Критически важно, что этот сценарий магниторезистивного действия во многом зависит от геометрии устройства и линий тока и не зависит от магнитных материалов.

В полупроводник с одним типом носителя магнитосопротивление пропорционально (1 + (мкБ)²), где μ - подвижность полупроводников (ед. м²· V⁻¹· С⁻¹ или T⁻¹) и B магнитное поле (ед. теслас). Антимонид индия, пример полупроводника с высокой подвижностью, может иметь подвижность электронов более 4 м²· V⁻¹· С⁻¹ при 300 К. Так, например, в поле 0,25 Тл увеличение магнитосопротивления будет 100%.

Анизотропное магнитосопротивление (AMR)

Устойчивость тонкого Пермаллой пленка показана здесь как функция угла приложенного внешнего поля.

Эксперименты Томсона^[4] являются примером AMR,^[7] свойство материала, в котором зависимость электрического сопротивления от угла между направлением электрического тока и направлением намагничивание наблюдается. Эффект возникает из-за одновременного действия намагниченности и спин-орбитальное взаимодействие а его подробный механизм зависит от материала. Это может быть, например, из-за большей вероятности s-d-рассеяния электронов в направлении намагниченности (которое контролируется приложенным магнитным полем). Общий эффект (в большинстве материалов) заключается в том, что электрическое сопротивление имеет максимальное значение, когда направление тока параллельно приложенному магнитному полю. AMR новых материалов изучается, и в некоторых ферромагнитных соединениях урана наблюдаются величины до 50%.^[8]

В поликристаллических ферромагнетиках AMR может зависеть только от угла ${ displaystyle varphi = psi - theta}$ между намагниченностью и направлением тока и (пока удельное сопротивление материала можно описать тензором второго ранга) оно должно следовать^[9]

${ Displaystyle rho ( varphi) = rho _ { perp} + ( rho _ { parallel} - rho _ { perp}) cos ^ {2} varphi}$

куда ${ displaystyle rho}$ это (продольный) удельное сопротивление фильма и ${ displaystyle rho _ { parallel, perp}}$ удельные сопротивления для ${ displaystyle varphi = 0}$ и ${ displaystyle 90 ^ { circ}}$ , соответственно. Связанное с продольным сопротивлением, существует также поперечное удельное сопротивление, названное (несколько сбивающим с толку[1]) планарный эффект Холла. В монокристаллах удельное сопротивление ${ displaystyle rho}$ зависит также от ${ displaystyle psi, theta}$ индивидуально.

Чтобы компенсировать нелинейные характеристики и невозможность определения полярности магнитного поля, для датчиков используется следующая структура. Он состоит из полосок алюминия или золота, помещенных на тонкую пленку пермаллой (ферромагнитный материал, демонстрирующий эффект AMR), наклоненный под углом 45 °. Эта структура заставляет ток течь не по «легким осям» тонкой пленки, а под углом 45 °. Зависимость сопротивления теперь имеет постоянное смещение, которое линейно вокруг нулевой точки. Из-за своего внешнего вида этот тип сенсора называется «парикмахерская'.

Эффект AMR используется в большом количестве датчиков для измерения магнитного поля Земли (электронных компас), для измерения электрического тока (путем измерения магнитного поля, созданного вокруг проводника), для обнаружения движения и для определения линейного положения и угла. Крупнейшие производители датчиков AMR: Honeywell, Полупроводники NXP, STMicroelectronics, и Sensitec GmbH.

В качестве теоретических аспектов И. А. Кэмпбелл, А. Ферт и О. Жауль (CFJ) ^[10] получили выражение для отношения AMR для сплавов на основе Ni с использованием двухтоковой модели с s-s и s-d процессами рассеяния, где s - электрон проводимости, а d - 3d-состояния со спин-орбитальным взаимодействием. Коэффициент AMR выражается как

${ displaystyle { frac { Delta rho} { rho}} = { frac { rho _ { parallel} - rho _ { perp}} { rho _ { perp}}} = гамма ( альфа -1),}$

с ${ Displaystyle гамма = (3/4) (А / Ч) ^ {2}}$ и ${ displaystyle alpha = rho _ { downarrow} / rho _ { uparrow}}$ , куда ${ displaystyle A}$ , ${ displaystyle H}$ , и ${ displaystyle rho _ { sigma}}$ - константа спин-орбитального взаимодействия (так называемая ${ displaystyle zeta}$ ), обменное поле и удельное сопротивление для спина ${ displaystyle sigma}$ , соответственно. Кроме того, недавно Сатоши Кокадо и др.^[11]^[12] получили общее выражение отношения AMR для ферромагнетиков из 3d-переходных металлов, расширив теорию CFJ на более общую. Общее выражение можно применить и к полуметаллам.

Смотрите также

Сноски

1. (Обычный) эффект Холла меняет знак при инверсии магнитного поля, и это орбитальный эффект (не связанный со спином) из-за силы Лоренца. Поперечный AMR (планарный эффект Холла^[13]) не меняет знака и вызвано спин-орбитальное взаимодействие.

Рекомендации

^ А. Б. Пиппард: Магнитосопротивление в металлах, Издательство Кембриджского университета (1989)
^ Coleman, R.V .; Исин, А. (1966), "Магнитосопротивление в монокристаллах железа", Журнал прикладной физики, 37 (3): 1028–1029, Bibcode:1966JAP .... 37.1028C, Дои:10.1063/1.1708320
^ «Непреодолимое магнитосопротивление».
^ ^а ^б Томсон, В. (18 июня 1857 г.), «Об электродинамических качествах металлов: - Влияние намагничивания на электропроводность никеля и железа», Proc. Royal Soc. Лондон., 8: 546–550, Дои:10.1098 / rspl.1856.0144
^ Нобелевская премия по физике 2007 г., Nobel Media AB, 9 октября 2007 г., получено 25 июн 2014
^ Дж. Джулиани (2008). «Общий закон электромагнитной индукции». EPL. 81 (6): 60002. arXiv:1502.00502. Bibcode:2008EL ..... 8160002G. Дои:10.1209/0295-5075/81/60002. S2CID 14917438.
^ McGuire, T .; Поттер, Р. (1975). «Анизотропное магнитосопротивление в ферромагнитных 3d сплавах». (PDF). IEEE Transactions on Magnetics. 11 (4): 1018–1038. Bibcode:1975ИТМ .... 11.1018М. Дои:10.1109 / TMAG.1975.1058782.
^ Вишневский, П. (2007). «Гигантское анизотропное магнитосопротивление и магнитотермоэдс в кубических пниктидах урана 3: 4». Письма по прикладной физике. 90 (19): 192106. Bibcode:2007ApPhL..90s2106W. Дои:10.1063/1.2737904.
^ De Ranieri, E .; Rushforth, A.W .; Výborný, K .; Rana, U .; Ахмед, Э .; Campion, R.P .; Foxon, C.T .; Gallagher, B.L .; Irvine, A.C .; Wunderlich, J .; Юнгвирт, Т. (10 июня 2008 г.), «Литографически и электрически контролируемые эффекты деформации на анизотропное магнитосопротивление в (Ga, Mn) As», New J. Phys., 10 (6): 065003, arXiv:0802.3344, Bibcode:2008NJPh ... 10f5003D, Дои:10.1088/1367-2630/10/6/065003, S2CID 119291699
^ Кэмпбелл, И. А .; Fert, A .; Jaoul, О. (1970). «Анизотропия самопроизвольного сопротивления в сплавах на основе никеля». J. Phys. C. 3 (1S): S95 – S101. Bibcode:1970JPhC .... 3S..95C. Дои:10.1088 / 0022-3719 / 3 / 1S / 310.
^ Кокадо, Сатоши; Цунода, Масакиё; Харигая, Кикуо; Сакума, Акимаса (2012). «Эффекты анизотропного магнитосопротивления в Fe, Co, Ni, Fe4N и полуметаллическом ферромагнетике: систематический анализ». J. Phys. Soc. JPN. 81 (2): 024705-1–024705-17. arXiv:1111.4864. Bibcode:2012JPSJ ... 81b4705K. Дои:10.1143 / JPSJ.81.024705. S2CID 100002412.
^ Кокадо, Сатоши; Цунода, Масакиё (2013). «Эффект анизотропного магнитосопротивления: общее выражение отношения AMR и интуитивное объяснение знака отношения AMR». Расширенные исследования материалов. 750-752: 978–982. arXiv:1305.3517. Bibcode:2013arXiv1305.3517K. Дои:10.4028 / www.scientific.net / AMR.750-752.978. S2CID 35733115.
^ Tang, H. X .; Kawakami, R.K .; Awschalom, D. D .; Роукс, М. Л. (март 2003 г.), «Гигантский планарный эффект Холла в эпитаксиальных (Ga, Mn) устройствах» (PDF), Phys. Rev. Lett., 90 (10): 107201, arXiv:cond-mat / 0210118, Bibcode:2003PhRvL..90j7201T, Дои:10.1103 / PhysRevLett.90.107201, PMID 12689027, S2CID 1485882

[1] А. Б. Пиппард: Магнитосопротивление в металлах, Издательство Кембриджского университета (1989)

[Coleman-2] Coleman, R.V .; Исин, А. (1966), "Магнитосопротивление в монокристаллах железа", Журнал прикладной физики, 37 (3): 1028–1029, Bibcode:1966JAP .... 37.1028C, Дои:10.1063/1.1708320

[3] «Непреодолимое магнитосопротивление».

[Kelvin-4] а ^б Томсон, В. (18 июня 1857 г.), «Об электродинамических качествах металлов: - Влияние намагничивания на электропроводность никеля и железа», Proc. Royal Soc. Лондон., 8: 546–550, Дои:10.1098 / rspl.1856.0144

[5] Нобелевская премия по физике 2007 г., Nobel Media AB, 9 октября 2007 г., получено 25 июн 2014

[Giuliani-6] Дж. Джулиани (2008). «Общий закон электромагнитной индукции». EPL. 81 (6): 60002. arXiv:1502.00502. Bibcode:2008EL ..... 8160002G. Дои:10.1209/0295-5075/81/60002. S2CID 14917438.

[McGuirePotter-7] McGuire, T .; Поттер, Р. (1975). «Анизотропное магнитосопротивление в ферромагнитных 3d сплавах». (PDF). IEEE Transactions on Magnetics. 11 (4): 1018–1038. Bibcode:1975ИТМ .... 11.1018М. Дои:10.1109 / TMAG.1975.1058782.

[Wiśniewski-8] Вишневский, П. (2007). «Гигантское анизотропное магнитосопротивление и магнитотермоэдс в кубических пниктидах урана 3: 4». Письма по прикладной физике. 90 (19): 192106. Bibcode:2007ApPhL..90s2106W. Дои:10.1063/1.2737904.

[9] De Ranieri, E .; Rushforth, A.W .; Výborný, K .; Rana, U .; Ахмед, Э .; Campion, R.P .; Foxon, C.T .; Gallagher, B.L .; Irvine, A.C .; Wunderlich, J .; Юнгвирт, Т. (10 июня 2008 г.), «Литографически и электрически контролируемые эффекты деформации на анизотропное магнитосопротивление в (Ga, Mn) As», New J. Phys., 10 (6): 065003, arXiv:0802.3344, Bibcode:2008NJPh ... 10f5003D, Дои:10.1088/1367-2630/10/6/065003, S2CID 119291699

[CFJ-10] Кэмпбелл, И. А .; Fert, A .; Jaoul, О. (1970). «Анизотропия самопроизвольного сопротивления в сплавах на основе никеля». J. Phys. C. 3 (1S): S95 – S101. Bibcode:1970JPhC .... 3S..95C. Дои:10.1088 / 0022-3719 / 3 / 1S / 310.

[Kokado1-11] Кокадо, Сатоши; Цунода, Масакиё; Харигая, Кикуо; Сакума, Акимаса (2012). «Эффекты анизотропного магнитосопротивления в Fe, Co, Ni, Fe4N и полуметаллическом ферромагнетике: систематический анализ». J. Phys. Soc. JPN. 81 (2): 024705-1–024705-17. arXiv:1111.4864. Bibcode:2012JPSJ ... 81b4705K. Дои:10.1143 / JPSJ.81.024705. S2CID 100002412.

[Kokado2-12] Кокадо, Сатоши; Цунода, Масакиё (2013). «Эффект анизотропного магнитосопротивления: общее выражение отношения AMR и интуитивное объяснение знака отношения AMR». Расширенные исследования материалов. 750-752: 978–982. arXiv:1305.3517. Bibcode:2013arXiv1305.3517K. Дои:10.4028 / www.scientific.net / AMR.750-752.978. S2CID 35733115.

[13] Tang, H. X .; Kawakami, R.K .; Awschalom, D. D .; Роукс, М. Л. (март 2003 г.), «Гигантский планарный эффект Холла в эпитаксиальных (Ga, Mn) устройствах» (PDF), Phys. Rev. Lett., 90 (10): 107201, arXiv:cond-mat / 0210118, Bibcode:2003PhRvL..90j7201T, Дои:10.1103 / PhysRevLett.90.107201, PMID 12689027, S2CID 1485882

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

Navigation