WikiDer > Баланс массы

А баланс массы, также называемый материальный баланс, это приложение сохранение массы анализу физических систем. Учет поступления материалов в систему и выхода из нее, массовые потоки можно идентифицировать то, что могло быть неизвестно или было трудно измерить без этого метода. Точный закон сохранения используемый в анализе системы, зависит от контекста проблемы, но все они вращаются вокруг сохранения массы, т.е. иметь значение не может исчезнуть или возникнуть спонтанно.^[1]:59–62

Поэтому массовые балансы широко используются в инженерное дело и экологический анализ. Например, теория баланса массы используется для проектирования химические реакторы, для анализа альтернативных процессов производства химикатов, а также для моделирования загрязнение дисперсия и другие процессы физических систем. Тесно связанные и дополнительные методы анализа включают баланс населения, энергетический баланс и несколько более сложный энтропия баланс. Эти методы необходимы для тщательного проектирования и анализа таких систем, как цикл охлаждения.

В экологическом мониторинге термин бюджетные расчеты используется для описания уравнений баланса массы, где они используются для оценки данных мониторинга (сравнение входных и выходных данных и т. д.). В биологии динамический энергетический бюджет Теория метаболической организации явно использует баланс массы и энергии.

Вступление

Общая форма баланса масс: Масса, которая входит в систему, должна, в силу сохранения массы, либо покинуть систему, либо накапливаться в системе..

Математически баланс массы для системы без химической реакции выглядит следующим образом:^[1]:59–62

${ displaystyle mathrm {Input} = mathrm {Output} + mathrm {Accumulation} ,}$

Строго говоря, это уравнение справедливо и для систем с химические реакции если термины в уравнении баланса относятся к общей массе, то есть к сумме всех химических компонентов системы. В отсутствие химической реакции количество входящих и исходящих химических веществ будет одинаковым; это приводит к уравнению для каждого вида, присутствующего в системе. Однако, если это не так, тогда в уравнение баланса массы необходимо внести поправки, чтобы учесть образование или истощение (потребление) каждого химического вещества. Некоторые используют один член в этом уравнении для учета химических реакций, которые будут отрицательными для истощения и положительными для генерации. Однако обычная форма этого уравнения написана для учета как положительного члена образования (то есть продукта реакции), так и отрицательного члена потребления (реагентов, используемых для производства продуктов). Хотя в целом один член будет учитывать общий баланс в системе, если это уравнение баланса должно применяться к отдельному виду, а затем ко всему процессу, оба члена необходимы. Это модифицированное уравнение можно использовать не только для реактивных систем, но и для баланса населения, например, в механика частиц проблемы. Уравнение приведено ниже; обратите внимание, что оно упрощается до более раннего уравнения в случае, если член генерации равен нулю.^[1]:59–62

${ displaystyle { text {Input}} + { text {Generation}} = { text {Output}} + { text {Accumulation}} + { text {Потребление}}}$

• В отсутствие ядерная реакция количество атомы приток и отток должны оставаться неизменными даже при наличии химической реакции.
• Для формирования баланса необходимо четко определить границы системы.
• Массовые балансы могут использоваться в физических системах в различных масштабах.
• Массовые балансы можно упростить, предположив, что устойчивое состояние, в котором срок накопления равен нулю.

Наглядный пример

Схема, показывающая пример осветлителя

Простой пример может проиллюстрировать эту концепцию. Рассмотрим ситуацию, в которой суспензия течет в отстойник для удаления твердых частиц из резервуара. Твердые частицы собираются внизу с помощью конвейерная лента частично погружен в резервуар, и вода выходит через сливное отверстие.

В этом примере есть два вещества: твердые вещества и вода. Выходное отверстие для перелива воды несет повышенную концентрацию воды относительно твердых частиц по сравнению с входным отверстием для суспензии, а выходное отверстие конвейерной ленты несет повышенную концентрацию твердых частиц по сравнению с водой.

Предположения

• Устойчивое состояние
• Безреактивная система

Анализ

Предположим, что состав входящего шлама (по массе) состоит из 50% твердого вещества и 50% воды с массовым расходом 100 кг/мин. Предполагается, что резервуар работает в установившемся режиме, и поэтому накопление равно нулю, поэтому вход и выход должны быть одинаковыми как для твердых частиц, так и для воды. Если мы знаем, что эффективность удаления для бака навозной жижи составляет 60%, то выпускное отверстие для воды будет содержать 20 кг/мин твердых частиц (40% раз 100 кг/мин раз 50% твердых веществ). Если мы измеряем расход объединенных твердых частиц и воды, и выход воды окажется равным 65 кг/мин, то количество воды, выходящей через конвейерную ленту, должно быть 5 кг/мин. Это позволяет нам полностью определить, как масса была распределена в системе, имея только ограниченную информацию и используя соотношения баланса массы через границы системы. Баланс массы для этой системы можно описать в виде таблицы:

Массовая обратная связь (переработка)

Градирни - хороший пример системы рециркуляции

Массовые балансы могут выполняться в системах с циклическими потоками. В этих системах выходные потоки возвращаются на вход установки, часто для дальнейшей обработки.^[1]:97–105

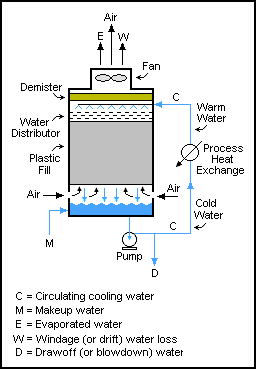
Такие системы распространены в шлифование контуры, где зерно измельчается, а затем просеивается, чтобы позволить только мелким частицам выйти из контура, а более крупные частицы возвращаются в вальцовую мельницу (мельницу). Однако потоки рециркуляции никоим образом не ограничиваются операциями механики твердого тела; они также используются в потоках жидкости и газа. Один из таких примеров есть в градирни, где вода многократно перекачивается через градирню, при этом при каждом проходе отбирается лишь небольшое количество воды (для предотвращения накопления твердых частиц) до тех пор, пока она не испарится или не выйдет вместе с отводимой водой. Баланс массы воды равен M = D + W + E.

Использование рециркуляции помогает увеличить общую конверсию исходных продуктов, что полезно для процессов конверсии с низким числом проходов (таких как Процесс Габера).

Дифференциальные массовые балансы

Также можно взять баланс массы по-разному. Концепция такая же, как и для большого баланса массы, но выполняется в контексте системы ограничений (например, можно рассматривать предельный случай по времени или, чаще, по объему). Дифференциальный баланс массы используется для создания дифференциальные уравнения которые могут предоставить эффективный инструмент для моделирования и понимания целевой системы.

Дифференциальный баланс массы обычно решается в два этапа: сначала необходимо получить набор основных дифференциальных уравнений, а затем эти уравнения должны быть решены либо аналитически, либо, для менее решаемых задач, численно.

Следующие системы являются хорошими примерами применения дифференциального баланса масс:

1. Идеальный (перемешиваемый) реактор периодического действия
2. Идеальный бак-реактор, также называемый Реактор с непрерывным перемешиванием (CSTR)
3. Идеально Реактор поршневого потока (PFR)

Идеальный реактор периодического действия

Идеальный реактор периодического действия с полностью перемешиванием представляет собой замкнутую систему. Изотермические условия предполагаются, и смешивание предотвращает градиенты концентрации, поскольку концентрации реагентов уменьшаются, а концентрации продукта увеличиваются с течением времени.^[2]:40–41 Многие учебники химии неявно предполагают, что изучаемую систему можно описать как реактор периодического действия, когда пишут о кинетике реакции и химическое равновесие.Массовый баланс вещества А становится

${ Displaystyle mathrm {IN} + mathrm {PROD} = mathrm {OUT} + mathrm {ACC}}$

${ displaystyle 0 + r _ { mathrm {A}} V = 0 + { frac {dn _ { mathrm {A}}} {dt}}}$

куда р_А обозначает скорость, с которой производится вещество А, V это объем (который может быть постоянным или нет), п_А количество родинок (п) вещества А.

В реактор периодического действия с подпиткой некоторые реагенты / ингредиенты добавляются непрерывно или импульсами (сравните приготовление каши, сначала смешивая все ингредиенты, а затем давая ей закипеть, что можно описать как реактор периодического действия, либо сначала смешивая только воду и соль и доведение до кипения перед добавлением других ингредиентов, что можно описать как реактор периодического действия с подпиткой). Балансы массы для реакторов периодического действия с подпиткой становятся немного сложнее.

Реактивный пример

В первом примере мы покажем, как использовать баланс масс для определения отношения между процент избытка воздуха для горение жидкого топлива на углеводородной основе и процентного содержания кислорода в газе продуктов сгорания. Во-первых, нормальный сухой воздух содержит 0.2095 моль кислорода на моль воздуха, поэтому на один моль О
₂ в 4,773 моль сухого воздуха. Для стехиометрического горения отношения между массой воздуха и массой каждого горючего элемента в жидком топливе следующие:

${ displaystyle { text {Carbon:}} { frac { text {масса воздуха}} { text {масса C}}} = { frac {4,773 times 28,96} {12.01}} = 11,51}$

${ displaystyle { text {Водород:}} { frac { text {масса воздуха}} { text {масса H}}} = { frac {{ frac {1} {4}} (4,773 ) times 28,96} {1,008}} = 34,28}$

${ displaystyle { text {Sulphur:}} { frac { text {масса воздуха}} { text {масса S}}} = { frac {4.773 times 28.96} {32.06}} = 4.31}$

Учитывая точность типичных аналитических процедур, уравнение массы воздуха на массу топлива при стехиометрическом сгорании выглядит следующим образом:

${ Displaystyle { frac { mathrm {масса воздуха}} { mathrm {масса топлива}}} = AFR_ {масса} = 11,5 (wC) +34,3 (wH) + (wS-wO) }$

где wC, wH, wS и wO относятся к массовой доле каждого элемента в жидком топливе, при сжигании серы до SO2 и AFR._масса относится к соотношение воздух-топливо в единицах массы.

За 1 кг Для жидкого топлива, содержащего 86,1% C, 13,6% H, 0,2% O и 0,1% S, стехиометрическая масса воздуха равна 14,56 кг, поэтому AFR = 14,56. Тогда масса продуктов сгорания равна 15.56 кг. При точной стехиометрии О
₂ должно отсутствовать. При 15-процентном избытке воздуха AFR = 16,75, а масса газообразных продуктов сгорания равна 17,75 кг, который содержит 0,505 кг избытка кислорода. Таким образом, горючие газы содержат 2,84% О
₂ по массе. Соотношение между процентом избытка воздуха и процентомО
₂ в дымовых газах точно выражаются квадратными уравнениями, действительными в диапазоне 0–30 процентов избытка воздуха:

${ Displaystyle mathrm {\% избыток воздух} = 1,2804 раз ( mathrm {\% O_ {2} in горение газ}) ^ {2} +4,49 раз ( mathrm {\% O_ {2} in горение газ})}$

${ Displaystyle mathrm {\% O_ {2} in сгорание газ} = -0,00138 раз ( mathrm {\% избыток воздух}) ^ {2} +0,210 раз ( mathrm {\% избыток воздух})}$

Во втором примере мы будем использовать закон массового действия к выводить выражение для химическое равновесие постоянный.

Предположим, у нас есть закрытый реактор, в котором протекает следующая жидкофазная обратимая реакция:

${ displaystyle a mathrm {A} + b mathrm {B} leftrightarrow c mathrm {C} + d mathrm {D}}$

Баланс массы для вещества A становится

${ Displaystyle mathrm {IN} + mathrm {PROD} = mathrm {OUT} + mathrm {ACC}}$

${ displaystyle 0 + r _ { mathrm {A}} V = 0 + { frac {dn _ { mathrm {A}}} {dt}}}$

Поскольку у нас есть жидкофазная реакция, мы можем (обычно) предполагать постоянный объем, и поскольку ${ Displaystyle п _ { mathrm {A}} = V * C _ { mathrm {A}}}$ мы получили

${ displaystyle r _ { mathrm {A}} V = V { frac {dC _ { mathrm {A}}} {dt}}}$

или же

${ displaystyle r _ { mathrm {A}} = { frac {dC _ { mathrm {A}}} {dt}}}$

Во многих учебниках это дается как определение скорость реакции без указания неявного предположения, что речь идет о скорости реакции в замкнутой системе только с одной реакцией. Это досадная ошибка, которая на протяжении многих лет сбивала с толку многих студентов.

Согласно закон массового действия скорость прямой реакции можно записать как

${ displaystyle r_ {1} = k_ {1} [ mathrm {A}] ^ {a} [ mathrm {B}] ^ {b}}$

и скорость обратной реакции как

${ Displaystyle г _ {- 1} = к _ {- 1} [ mathrm {C}] ^ {c} [ mathrm {D}] ^ {d}}$

Таким образом, скорость производства вещества А

${ Displaystyle г _ { mathrm {A}} = а (г _ {- 1} -r_ {1})}$

и поскольку в состоянии равновесия концентрация A постоянна, мы получаем

${ displaystyle r _ { mathrm {A}} = a (r _ {- 1} -r_ {1}) = { frac {dC _ { mathrm {A}}} {dt}} = 0}$

или, переставил

${ displaystyle { frac {k_ {1}} {k _ {- 1}}} = { frac {[ mathrm {C}] ^ {c} [ mathrm {D}] ^ {d}} {[ mathrm {A}] ^ {a} [ mathrm {B}] ^ {b}}} = K_ {экв}}$

Идеальный резервуарный реактор / резервуарный реактор с непрерывным перемешиванием

Резервуарный реактор с непрерывным смешиванием представляет собой открытую систему с входящим потоком реагентов и выходящим потоком продуктов.^[2]:41 Озеро можно рассматривать как резервуарный реактор, а озера с большим временем оборота (например, с низким отношением потока к объему) для многих целей можно рассматривать как непрерывно перемешиваемые (например, однородные во всех отношениях). Тогда баланс массы становится

${ Displaystyle mathrm {IN} + mathrm {PROD} = mathrm {OUT} + mathrm {ACC}}$

${ displaystyle Q_ {0} cdot C _ { mathrm {A}, 0} + r _ { rm {A}} cdot V = Q cdot C _ { mathrm {A}} + { frac {dn_ { mathrm {A}}} {dt}}}$

куда Q₀ и Q обозначают объемный расход в системе и из системы соответственно и C_{А, 0} и C_А концентрация A на входе и выходе соответственно. В открытой системе мы никогда не сможем достичь химического равновесия. Однако мы можем достичь устойчивое состояние где все переменные состояния (температура, концентрации и т. д.) остаются постоянными (${ displaystyle mathrm {ACC} = 0}$).

Пример

Рассмотрим ванну, в которой растворено немного соли для купания. Теперь мы наливаем больше воды, не закрывая нижнюю пробку. Что происходит?

Поскольку реакции нет, ${ displaystyle mathrm {PROD} = 0}$ а так как оттока нет ${ displaystyle Q = 0}$. Баланс массы становится

${ Displaystyle mathrm {IN} + mathrm {PROD} = mathrm {OUT} + mathrm {ACC}}$

${ displaystyle Q_ {0} cdot C _ { mathrm {A}, 0} + 0 = 0 cdot C _ { mathrm {A}} + { frac {dn _ { mathrm {A}}} {dt} }}$

или же

${ displaystyle Q_ {0} cdot C _ { mathrm {A}, 0} = { frac {dC _ { mathrm {A}} V} {dt}} = V { frac {dC _ { mathrm {A }}} {dt}} + C _ { mathrm {A}} { frac {dV} {dt}}}$

Однако, используя баланс массы для общего объема, очевидно, что ${ displaystyle { frac {dV} {dt}} = Q_ {0}}$и это ${ Displaystyle V = V_ {t = 0} + Q_ {0} t}$. Таким образом мы получаем

${ displaystyle { frac {dC _ { mathrm {A}}} {dt}} = { frac {Q_ {0}} {(V_ {t = 0} + Q_ {0} t)}} left ( C _ { mathrm {A}, 0} -C _ { mathrm {A}} right)}$

Обратите внимание, что реакции нет и, следовательно, нет скорость реакции или же тарифный закон вовлечен, и все же ${ displaystyle { frac {dC _ { mathrm {A}}} {dt}} neq 0}$. Таким образом, можно сделать вывод, что скорость реакции нельзя определить в общем виде, используя ${ displaystyle { frac {dC} {dt}}}$. Один должен сначала запишите баланс массы перед установкой связи между ${ displaystyle { frac {dC} {dt}}}$ и скорость реакции можно найти. Однако во многих учебниках скорость реакции определяется как

${ displaystyle r = { frac {dC _ { mathrm {A}}} {dt}}}$

без упоминания того, что это определение неявно предполагает, что система замкнута, имеет постоянный объем и что существует только одна реакция.

Идеальный поршневой реактор (PFR)

Идеализированный реактор с поршневым потоком представляет собой открытую систему, напоминающую трубу, без перемешивания в направлении потока, но с идеальным перемешиванием перпендикулярно направлению потока, часто используемую в таких системах, как реки и водопроводные трубы, если поток является турбулентным. Когда выполняется баланс массы трубки, в первую очередь учитывается бесконечно малый часть трубы и произведите баланс масс, используя идеальную модель реактора резервуара.^[2]:46–47 Тогда этот баланс массы интегрированный по всему объему реактора, чтобы получить:

${ displaystyle { frac {d (Q cdot C _ { rm {A}})} {dV}} = r _ { rm {A}}}$

В числовых решениях, например при использовании компьютеров идеальная труба часто преобразуется в серию резервуарных реакторов, поскольку можно показать, что PFR эквивалентен бесконечному количеству последовательно соединенных резервуаров с мешалкой, но последний часто легче анализировать, особенно в установившемся режиме. .

Более сложные проблемы

В действительности реакторы часто неидеальны, и для описания системы используются комбинации приведенных выше моделей реакторов. Не только скорости химических реакций, но и массообмен ставки могут быть важны при математическом описании системы, особенно в неоднородный системы.^[3]

Как химический скорость реакции в зависимости от температуры часто бывает необходимо сделать как энергетический баланс (часто это тепловой баланс, а не полноценный энергетический баланс), а также массовые балансы для полного описания системы. Для энергетического баланса может потребоваться другая модель реактора: закрытая по массе система может быть открытой по энергии, например. поскольку тепло может попасть в систему через проводимость.

Коммерческое использование

В промышленных технологических установках, используя тот факт, что масса, входящая и выходящая из любой части технологической установки, должна уравновешиваться, проверка и согласование данных могут использоваться алгоритмы для корректировки измеренных потоков при условии, что существует достаточная избыточность измерений потока, позволяющая статистическое согласование и исключение обнаруживаемых ошибочных измерений. Поскольку все измеренные значения реального мира содержат неотъемлемую погрешность, согласованные измерения обеспечивают лучшую основу, чем измеренные значения, для финансовой отчетности, оптимизации и нормативной отчетности. Пакеты программного обеспечения существуют, чтобы сделать это коммерчески осуществимым на ежедневной основе.

Смотрите также

Рекомендации

внешняя ссылка

• Расчеты материального баланса
• Основы материального баланса
• Материальный баланс химических реакторов
• Материально-энергетический баланс
• Метод теплового и материального баланса для управления технологическим процессом на нефтехимических и нефтеперерабатывающих заводах, Патент США 6751527
• Моррис, Артур Э .; Гейгер, Гордон; Хорошо, Х. Алан (2011). Справочник по расчетам материально-энергетического баланса при обработке материалов (3-е изд.). Wiley. ISBN 978-1-118-06565-5.