WikiDer > Мембранные вычисления

Мембранные вычисления (или же MC) - это область внутри Информатика который стремится открыть для себя новое вычислительные модели из изучения биологических клетки, особенно клеточные мембраны. Это подзадача создания сотовая модель.

Мембранные вычисления имеют дело с моделями распределенных и параллельных вычислений, обрабатывая мультимножества объектов символов локализованным образом. Таким образом, правила эволюции позволяют инкапсулировать развивающиеся объекты в отсеки, определяемые мембранами. Связь между отсеками и окружающей средой играет важную роль в процессах. Различные типы мембранных систем известны как Системы P после Георге Пэун кто первым задумал модель в 1998 году.^[1]

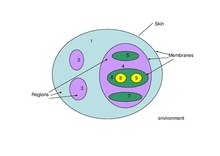
Важный ингредиент Система P это его мембранная структура, которая может быть иерархическим расположением мембран, как в клетке, или сеткой мембран (помещенных в узлы графа), как в ткани или нейронной сети. Системы P часто изображаются графически с рисунками.

Девятирегиональный мембранный компьютер

Интуиция, лежащая в основе понятия мембраны, - это трехмерный пузырь из биологии. Однако сама концепция является более общей, и мембрана рассматривается как разделитель двух областей. Мембрана обеспечивает избирательную связь между двумя областями. По словам Георгия Пэуна, разделение связано с Евклидово пространство в конечное «внутреннее» и бесконечное «внешнее». Выборочная коммуникация - вот где нужны вычисления.

Графические представления могут содержать множество элементов в зависимости от разновидности модели, которая изучается. Например, правило может создавать специальный символ δ, и в этом случае содержащая его мембрана растворяется, и все ее содержимое перемещается вверх по иерархии регионов.

Разнообразие предложений из биологии и диапазон возможностей для определения архитектуры и функционирования устройства обработки мультимножества на основе мембран практически безграничны. Действительно, литература по мембранным вычислениям содержит очень большое количество моделей. Таким образом, MC - это не просто теория, относящаяся к конкретной модели, это основа для разработки раздельных моделей.

Химические вещества моделируются символами или, альтернативно, цепочками символов. Область, которая определяется мембраной, может содержать другие символы или строки (вместе именуемые объектами) или другие мембраны, так что Система P имеет ровно одну внешнюю мембрану, называемую кожной мембраной, и иерархические отношения, управляющие всеми ее мембранами под кожной мембраной.

Если объекты являются символами, то имеет значение их множественность в пределах региона; однако в некоторых струнных моделях также используются мультинаборы. У регионов есть связанные правила, которые определяют, как объекты производятся, потребляются, передаются в другие регионы и иным образом взаимодействуют друг с другом. Недетерминированное максимально параллельное применение правил во всей системе - это переход между состояниями системы, а последовательность переходов называется вычислением. Можно определить конкретные цели для обозначения состояния остановки, при котором результатом вычисления будут объекты, содержащиеся в определенной области. В качестве альтернативы результат может состоять из предметов, отправленных из кожной мембраны в окружающую среду.

Было изучено много вариантов моделей, и интерес был сосредоточен на доказательстве вычислительной универсальности для систем с небольшим количеством мембран с целью решения NP-полных задач, таких как Проблемы логической выполнимости (SAT) и задача коммивояжера (TSP). В Системы P могут обмениваться сложностями в пространстве и времени и реже использовать модели для объяснения естественных процессов в живых клетках. В ходе исследований разрабатываются модели, которые, по крайней мере, теоретически могут быть реализованы на оборудовании. На сегодняшний день Системы P почти все теоретические модели, которые никогда не сводились к практике, хотя практическая система дана в.^[2]

Смотрите также

• Моделирование биологических систем

Рекомендации