WikiDer > Молекулярный демон
А Молекулярный демон или же биологическая молекулярная машина это биологический макромолекула который похож и имеет те же свойства, что и Демон Максвелла. Эти макромолекулы собираются Информация чтобы признать их субстрат или же лиганд в мириадах других молекул, плавающих во внутриклеточной или внеклеточной плазме. Этот молекулярное распознавание представляет собой прирост информации, который эквивалентен приросту энергии или уменьшению энтропия. Когда демон сбрасывается, т.е. когда лиганд высвобождается, информация стирается, энергия рассеивается и энтропия увеличивается в соответствии с второй закон термодинамики.[1] Разница между биологическими молекулярными демонами и мысленным экспериментом демона Максвелла заключается в явном нарушении последним второго закона.[2][3]
Цикл
Молекулярный демон переключается в основном между двумя конформации. Первое, или основное состояние, при распознавании и связывании лиганда или субстрата после индуцированный припадок, претерпевает изменение конформации, которое приводит ко второму квазистабильному состоянию: белок-лигандный комплекс. Чтобы сбросить белок в исходное, основное состояние, ему необходимо АТФ. Когда АТФ потребляется или гидролизуется, лиганд высвобождается, и демон снова получает информацию, возвращаясь в свое основное состояние. Цикл может начаться снова[1].
Трещотка
Второй закон термодинамики - это статистический закон. Следовательно, иногда отдельные молекулы могут не подчиняться закону. Все молекулы подвержены молекулярной буре, т. Е. Случайному движению молекул в цитоплазма и внеклеточной жидкости. Молекулярные демоны или молекулярные машины либо биологические, либо искусственно созданные, непрерывно толкаются случайным тепловым движением в направлении, которое иногда нарушает закон. Когда это происходит, и можно предотвратить скольжение макромолекулы назад от движения, которое она совершила, или конформационное изменение, которому она претерпела, в исходное состояние, как в случае с молекулярными демонами, молекула работает как храповик.[4][5]; можно наблюдать, например, создание градиент ионов или других молекул через клеточная мембрана, движение моторные белки вдоль белков филаментов или накопление продуктов ферментативной реакции. Даже некоторые искусственные молекулярные машины и эксперименты способны образовывать храповик, явно противоречащий второму закону термодинамики.[6][7]. Все эти молекулярные демоны должны быть возвращены в исходное состояние, потребляя внешнюю энергию, которая впоследствии рассеивается в виде тепла. Следовательно, этот последний шаг, на котором увеличивается энтропия, необратим. Если бы демоны были обратимы, работы не было бы[5].
Искусственный
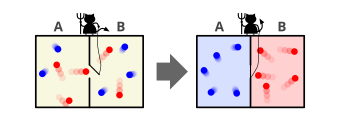
Примером искусственных трещоток является работа Серрели и др. (2007)[6]. Серрели и др. построил наномашина, а ротаксан, который состоит из молекулы в форме кольца, которая движется по крошечной оси молекулы между двумя разными равными отсеками, A и B. Нормальное, случайное движение молекул отправляет кольцо назад и вперед. Поскольку кольца перемещаются свободно, половина ротаксанов имеет кольцо на участке B, а другая половина - на участке A. Но система, используемая Serreli et al. имеет химический затвор на молекуле ротаксана, а ось содержит две липкие части, по одной с каждой стороны затвора. Эти ворота открываются, когда кольцо близко. Липкая часть в B находится близко к воротам, и кольца легче проходят к A, чем от A к B. Они получили отклонение от равновесия 70:50 для A и B соответственно, что немного похоже на демона Максвелла. Но эта система работает только тогда, когда на нее попадает свет, и поэтому требуется внешняя энергия, как молекулярные демоны.
Энергия и информация
Ландауэр заявил, что информация носит физический характер.[8] Его принцип устанавливает фундаментальные термодинамические ограничения для классической и квантовой обработки информации. Много усилий было направлено на включение информации в термодинамику и измерение энтропийных и энергетических затрат на манипулирование информацией. Получение информации снижает энтропию, что требует затрат энергии. Эта энергия должна собираться из окружающей среды.[9] Ландауэр установил эквивалентность одного бита информации энтропии, которая представлена как kT ln 2, где k - постоянная Больцмана, а T - комнатная температура. Эта оценка называется пределом Ландауэра.[10] Стирание энергии вместо этого увеличивает энтропию[11]. Toyabe et al. (2010) смогли экспериментально продемонстрировать, что информацию можно преобразовать в свободную энергию. Это довольно элегантный эксперимент, состоящий из микроскопической частицы на потенциале, напоминающем спиральную лестницу. Ступенька имеет высоту, соответствующую kBТ, где kB это Постоянная Больцмана Т - температура. Частица перескакивает между ступенями из-за случайных тепловых движений. Поскольку скачки вниз по градиенту происходят чаще, чем вверх, частица в среднем падает с лестницы. Но когда наблюдается скачок вверх, за частицей помещается блок, чтобы предотвратить ее падение, как в храповике. Таким образом он должен подниматься по лестнице. Информация получается путем измерения местоположения частицы, что эквивалентно увеличению энергии, то есть уменьшению энтропии. Они использовали обобщенное уравнение для второго закона, которое содержит переменную для информации:
⟨ΔF− W⟩≤ kBTI
ΔF это свободная энергия между состояниями, Вт проделана ли работа в системе, kB постоянная Больцмана, Т это температура, и я это взаимная информация содержание получено путем измерений. В скобках указано, что энергия средняя.[7]. Они могли преобразовать эквивалент однобитовой информации в 0,28 kTln2 энергии или, другими словами, они могли бы использовать более четверти энергетического содержания информации[12].
Когнитивные демоны
В его книге Случайность и необходимость, Жак Моно описали функции белков и других молекул, способных распознавать с «выборочным различением» субстрат, лиганд или другую молекулу[2]. При описании этих молекул он ввел термин «когнитивные» функции, те же самые когнитивные функции, которые Максвелл приписывал своему демону. Вернер Левенштейн идет дальше и называет эти молекулы «молекулярный демон'или' демон 'короче[1].
Такое название биологических молекулярных машин упрощает понимание сходства между этими молекулами и демоном Максвелла.
Из-за этого реального отличительного, если не «когнитивного» свойства, Жак Моно приписал этим биологическим комплексам телеономическую функцию. Телеономия подразумевает идею ориентированной, последовательной и конструктивной деятельности. Следовательно, белки должны рассматриваться как важные молекулярные агенты в телеономической деятельности всех живых существ.
Смотрите также
Рекомендации
- ^ а б c Р., Левенштейн, Вернер (29 января 2013 г.). Физика в уме: квантовый взгляд на мозг. Нью-Йорк. ISBN 9780465029846. OCLC 778420640.
- ^ а б Монод Дж (1970). Le Hasard et la nécessité. Essai sur la естественная философия de la biologie moderne [Случайность и необходимость Очерк натурфилософии современной биологии] (На французском). Le Seuil.
- ^ Максвелл, Джеймс Клерк (2009). Научные статьи Джеймса Клерка Максвелла. Кембридж: Издательство Кембриджского университета. Дои:10.1017 / cbo9780511698095. ISBN 9780511698095.
- ^ Бломберг, Клас (2007), "БРАУНОВСКАЯ ТРЕЩЕТКА: ОДНОНАПРАВЛЕННЫЕ ПРОЦЕССЫ", Физика жизни, Elsevier, pp. 340–343, Дои:10.1016 / b978-044452798-1 / 50031-2, ISBN 9780444527981
- ^ а б М., Хоффманн, Питер (2012). Храповик жизни: как молекулярные машины извлекают порядок из хаоса. Основные книги. ISBN 9780465022533. OCLC 808107321.
- ^ а б Leigh, David A .; Юан Р. Кей; Ли, Чин-Фа; Серрели, Вивиана (01.02.2007). «Молекулярный информационный храповик». Природа. 445 (7127): 523–527. Дои:10.1038 / природа05452. ISSN 1476-4687. PMID 17268466.
- ^ а б Сано, Масаки; Мунеюки, Эйро; Уэда, Масахито; Сагава, Такахиро; Тоябе, Шоичи (14 ноября 2010 г.). «Экспериментальная демонстрация преобразования информации в энергию и подтверждение обобщенного равенства Ярзинского». Природа Физика. 6 (12): 988–992. arXiv:1009.5287. Дои:10.1038 / nphys1821. ISSN 1745-2481.
- ^ Ландауэр, Рольф (1991). «Информация физическая». Физика сегодня. 44 (5): 23–29. Дои:10.1063/1.881299.
- ^ Сагава, Такахиро; Horowitz, Jordan M .; Паррондо, Хуан М. Р. (03.02.2015). «Термодинамика информации». Природа Физика. 11 (2): 131–139. Дои:10.1038 / nphys3230. ISSN 1745-2481.
- ^ Альфонсо-Фаус, Антонио (30.06.2013). «Фундаментальный принцип преобразования информации в энергию». Arrivi.org: 4. arXiv:1401.6052.
- ^ Болл, Филипп (2012). «Выявлена неизбежная стоимость вычислений». Новости природы. Дои:10.1038 / природа.2012.10186.
- ^ «Информация преобразуется в энергию». Мир физики. 2010-11-19. Получено 2019-01-30.
