WikiDer > Плоскость поляризации

Период, термин плоскость поляризации относится к направлению поляризация из линейно-поляризованный свет или другое электромагнитное излучение. К сожалению, этот термин используется в двух противоположных значениях. Как первоначально определено Этьен-Луи Малюс в 1811 г.,[2] плоскость поляризации совпадала (хотя в то время это не было известно) с плоскостью, содержащей направление распространения и магнитный вектор.[3] В современной литературе термин плоскость поляризации, если он вообще используется, скорее всего, будет означать плоскость, содержащую направление распространения и электрический вектор,[4] потому что электрическое поле имеет большую склонность взаимодействовать с веществом.[5]
Для волн в двулучепреломляющий (дважды преломляющий) кристалл, согласно старому определению, необходимо также указать, означает ли направление распространения направление луча или волновое направление.нормальный направление, потому что эти направления обычно различаются и оба перпендикулярны магнитному вектору (рис. 1). Малус, как приверженец корпускулярная теория света, можно было выбрать только направление луча. Но Огюстен-Жан Френель, в его успешной попытке объяснить двойное лучепреломление под теория волн (1822 г. и далее), сочли более полезным выбрать направление нормали волны, в результате чего предполагаемые колебания среды были последовательно перпендикулярны плоскости поляризации.[6] В изотропный В такой среде, как воздух, направления лучей и нормали к волнам одинаковы, и модификация Френеля не имеет значения.
Френель также признал, что, если бы он не чувствовал себя ограниченным принятой терминологией, было бы более естественным определить плоскость поляризации как плоскость, содержащую колебания и направление распространения.[7] Тот самолет, который стал известен как самолет вибрация, перпендикулярна «плоскости поляризации» Френеля, но идентична плоскости, которую современные авторы склонны называть этим именем!
Утверждалось, что термин плоскость поляризациив оригинале следует избегать из-за его исторической двусмысленности. Можно легко указать ориентацию конкретного вектора поля; и даже термин плоскость вибрации несет меньше риска путаницы, чем плоскость поляризации.[8]
Физика термина
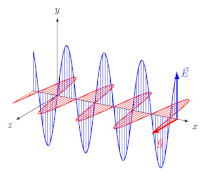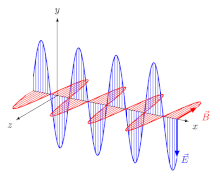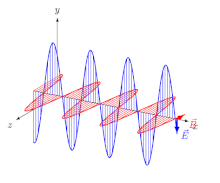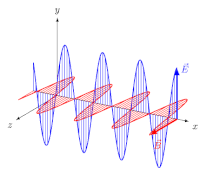
За электромагнитные (ЭМ) волны в изотропный среда (то есть среда, свойства которой не зависят от направления), электрическое поле векторов (E и D) идут в одном направлении, а магнитное поле векторы (B и ЧАС) находятся в другом направлении, перпендикулярном первому, а направление распространения перпендикулярно как электрическому, так и магнитному векторам. В этом случае направление распространения является как луч направление и волна нормальный направление (направление, перпендикулярное волновой фронт). Для линейно-поляризованный волна (также называемая самолет-поляризованная волна) ориентации векторов поля фиксированы (рис.2).
Потому что бесчисленные материалы диэлектрики или же проводники в то время как сравнительно мало ферромагнетики, то отражение или же преломление электромагнитных волн (в том числе свет) чаще всего из-за различий в электрический свойств носителей, чем различия в их магнитных свойствах. Это обстоятельство привлекает внимание к электрический векторов, поэтому мы склонны думать о направлении поляризации как о направлении электрических векторов, а «плоскость поляризации» как о плоскости, содержащей электрические векторы и направление распространения.

Действительно, это соглашение, используемое в онлайн- Британская энциклопедия,[4] И в Фейнманлекция о поляризации.[9] В последнем случае следует вывести соглашение из контекста: Фейнман продолжает подчеркивать направление электрический (E) вектор и оставляет читателю возможность предположить, что «плоскость поляризации» содержит этот вектор - и эта интерпретация действительно соответствует приведенным им примерам. Этот же вектор используется для описания поляризации радиосигналов и антенны (Рис. 3).[10]
Если среда магнитно изотропна, но электрически не-изотопный (как дважды преломляющий кристалл) магнитные векторы B и ЧАС по-прежнему параллельны, и электрические векторы E и D по-прежнему перпендикулярны обоим, а направление луча по-прежнему перпендикулярно E и магнитные векторы, а направление нормали волны все еще перпендикулярно D и магнитные векторы; но обычно существует небольшой угол между электрическими векторами E и D, следовательно, такой же угол между направлением луча и направлением нормали к волне (рис. 1).[1][11] Следовательно D, Eнаправление нормали к волнам и направление лучей находятся в одной плоскости, и тем более естественно определить эту плоскость как «плоскость поляризации».
Это «естественное» определение, однако, зависит от теории электромагнитных волн, развитой Джеймс Клерк Максвелл в 1860-е годы - тогда как слово поляризация был придуман примерно 50 лет назад, и загадка, связанная с ним, возникла еще раньше.
История термина
Три кандидата
Случайно или намеренно плоскость поляризации всегда определялась как плоскость, содержащая вектор поля и направление распространения. На рис.1 таких плоскостей три, которым мы можем присвоить номера для удобства:
- (1) плоскость, содержащая оба электрических вектора и оба направления распространения (т. Е. Плоскость, нормальная к магнитным векторам);
- (2а) плоскость, содержащая магнитные векторы и волновую нормаль (т. Е. Плоскость, нормальную к D);
- (2b) плоскость, содержащая магнитные векторы и луч (т. Е. Плоскость, нормальная к E).
В изотропной среде E и D иметь то же направление,[Примечание 1] так что направления лучей и нормалей волны сливаются, а плоскости (2a) и (2b) становятся одним целым:
- (2) плоскость, содержащая оба магнитных вектора и оба направления распространения (т. Е. Плоскость, нормальная к электрическим векторам).
Выбор малуса
Поляризация была открыта - но не названа и не понята - Кристиан Гюйгенс, поскольку он исследовал двойное лучепреломление «Исландский кристалл» (прозрачный кальцит, теперь называется Исландский лонжерон). Суть его открытия, опубликованного в его Трактат о свете (1690), заключалась в следующем. Когда луч (то есть узкий луч света) проходит через два одинаково ориентированных кристалла кальцита при нормальном падении, обычный луч, выходящий из первого кристалла, испытывает только обычное преломление во втором, в то время как необычный луч, выходящий из первого, страдает только необычайное преломление во втором. Но когда второй кристалл поворачивается на 90 ° вокруг падающих лучей, роли меняются местами, так что обычный луч, выходящий из первого кристалла, испытывает только необычайное преломление во втором, и наоборот. В промежуточных положениях второго кристалла каждый луч, выходящий из первого, дважды преломляется вторым, давая всего четыре луча; и когда кристалл поворачивается от первоначальной ориентации к перпендикулярной, яркость лучей изменяется, обеспечивая плавный переход между крайними случаями, в которых есть только два конечных луча.[12]
Гюйгенс определил главный раздел кристалла кальцита в виде плоскости, нормальной к естественной поверхности и параллельной оси тупого телесного угла.[13] Эта ось была параллельна осям сфероидальный вторичные волны которым он (правильно) объяснил направления необычайного преломления.
Период, термин поляризация был придуман Этьен-Луи Малюс в 1811 г.[2] В 1808 году, в разгар подтверждения геометрического описания двойного лучепреломления Гюйгенсом (при оспаривании его физического объяснения), Малус обнаружил, что когда луч света отражается от неметаллической поверхности под соответствующим углом, он ведет себя как один двух лучей, выходящих из кристалла кальцита.[14][Заметка 2] Поскольку это поведение ранее было известно только в связи с двойным лучепреломлением, Малус описал его в этом контексте. В частности, он определил плоскость поляризации поляризованного луча как плоскости, содержащей луч, в котором должна лежать основная часть кристалла кальцита, чтобы вызвать только обычный преломление.[15] Это определение было тем более разумным, потому что оно означало, что когда луч поляризуется отражением (от изотопной среды), плоскость поляризации является плоскость падения и отражение - то есть плоскость, содержащая падающий луч, нормаль к отражающей поверхности и поляризованный отраженный луч. Но, как мы теперь знаем, этот самолет содержит магнитный векторы поляризованного луча, а не электрические векторы.[16]
Плоскость луча и магнитных векторов пронумерованы (2b) над. Подразумевается, что плоскость поляризации содержит магнитный векторы все еще можно найти в определении, данном в онлайн-словаре Merriam-Webster.[17] Четное Джулиус Адамс Страттон, сказав, что "поляризацию принято определять в терминах E", тут же добавляет:" Однако в оптике ориентация векторов традиционно определяется "плоскостью поляризации", под которой понимается плоскость, нормальная к E содержащий оба ЧАС и ось распространения ».[10] Это определение совпадает с определением Малуса.
Выбор Френеля
В 1821 г. Огюстен-Жан Френель объявил свою гипотезу о том, что световые волны исключительно поперечный и поэтому всегда поляризованный в смысле наличия определенной поперечной ориентации, и то, что мы называем неполяризованный Фактически свет - это свет, ориентация которого быстро и беспорядочно меняется.[18] Предположим, что световые волны аналогичны поперечные волны в упругие твердые тела, и что выше показатель преломления соответствует высшему плотность из светоносный эфир, он обнаружил, что может объяснить частичное отражение (включая поляризацию за счет отражения) на границе раздела двух прозрачных изотропных сред при условии, что колебания эфира перпендикулярны плоскости поляризации.[19] Таким образом, поляризация, согласно полученному определению, находилась «в» определенной плоскости, если колебания были перпендикуляр в этот самолет!
Сам Френель счел этот вывод неудобным; позже в том же году он написал:
- Приняв эту гипотезу, было бы естественнее назвать плоскость поляризации той, в которой предполагается совершать колебания, но я не хотел вносить никаких изменений в полученные наименования.[7][Заметка 3]
Но вскоре он почувствовал себя обязанным сделать менее радикальное изменение. В его успешной модели двойного лучепреломления смещение среды было ограничено касательным к волновому фронту, в то время как сила могла отклоняться от смещения и от волнового фронта.[20] Следовательно, если колебания были перпендикулярны плоскости поляризации, то плоскость поляризации содержала нормаль волны, но не обязательно луч.[21] В своих «Вторых мемуарах» о двойном лучепреломлении Френель формально принял это новое определение, признав, что оно согласуется со старым определением в изотропной среде, такой как воздух, но не в двулучепреломляющем кристалле.[6]
Колебания, перпендикулярные плоскости поляризации Малуса, являются электрическими, а касательная к фронту волны электрическая вибрация равна D (Рисунок 1). Таким образом, с точки зрения вышеприведенной нумерации, Френель изменил «плоскость поляризации» с (2b) к (2а). Определение Френеля остается совместимым с определением Мерриама-Вебстера,[17] в котором не указано направление распространения. И это остается совместимым с определением Страттона,[10] потому что это дается в контексте изотропной среды, в которой плоскости (2a) и (2b) сливаются в (2).
То, что Френель назвал "более естественным" выбором, было самолетом, содержащим D и направление распространения. На рис. 1 единственная плоскость, отвечающая этой спецификации, - это плоскость, обозначенная как «плоскость вибрации» и позже пронумерованная (1) - то есть тот, который современное авторы склонны отождествлять себя с «плоскостью поляризации». Поэтому мы могли бы пожелать, чтобы Френель менее почтительно относился к своим предшественникам. Этот сценарий, однако, менее реалистичен, чем может показаться, потому что даже после того, как теория поперечных волн Френеля стала общепризнанной, направление колебаний было предметом постоянных споров.
«Плоскость вибрации»
Принцип, согласно которому показатель преломления зависит от плотности эфира, был существенным для теории Френеля. гипотеза сопротивления эфира.[22] Но его нельзя было распространить на кристаллы с двойным лучепреломлением, в которых по крайней мере один показатель преломления изменяется в зависимости от направления, потому что плотность не является направленной. Следовательно, его объяснение рефракции требовало изменения направления в жесткость эфира в двулучепреломляющая среда, плюс вариация плотности между средства массовой информации.[23]
Джеймс МакКаллах и Франц Эрнст Нойман избежать этого осложнения, предположив, что более высокий показатель преломления всегда соответствует той же плотности, но большей упругости согласие (меньшая жесткость). Чтобы получить результаты, согласующиеся с наблюдениями за частичным отражением, они должны были предположить, в отличие от Френеля, что колебания в плоскость поляризации.[24]
Вопрос требовал экспериментального определения направления вибрации, и на него ответил: Джордж Габриэль Стоукс. Он определил плоскость вибрации как «плоскость, проходящая через луч и направление вибрации»[25] (в соответствии с рис. 1). Теперь предположим, что штраф дифракционная решетка горит при нормальном падении. При больших углах дифракции решетка будет выглядеть несколько смещенной с ребра, так что направления колебаний будут сужены в направлении, параллельном плоскости решетки. Если плоскости поляризации совпадают с плоскостями вибрации (как сказали МакКуллаг и Нойман), они будут переполнены в одном направлении; и если плоскости поляризации нормальный к плоскостям вибрации (как сказал Френель), плоскости поляризации будут теснены в нормальном направлении. Чтобы найти направление скопления, можно было бы изменять поляризацию падающего света с равными шагами и определять плоскости поляризации дифрагированного света обычным способом. Стокс провел такой эксперимент в 1849 году, и он оказался в пользу Френеля.[25][26]
В 1852 году Стокс отметил гораздо более простой эксперимент, который приводит к такому же выводу. Солнечный свет, рассеянный на участке голубого неба под углом 90 ° от Солнца, с помощью методов Малуса обнаруживается как поляризованный в плоскости, содержащей луч зрения и Солнце. Но из геометрии очевидно, что колебания этого света могут быть только перпендикулярными этой плоскости.[27]
Однако в каком-то смысле МакКуллаг и Нойман были правы. Если мы попытаемся провести аналогию между поперечными волнами в неизотропном упругом твердом теле и электромагнитными волнами в магнитно-изотропном, но электрически неизотропном кристалле, плотность должна соответствовать магнитной проницаемость (оба являются ненаправленными), а соответствие должно соответствовать электрическому диэлектрическая проницаемость (оба являются направленными). В результате скорость твердого тела соответствует ЧАС поле,[28] так, чтобы механические колебания поперечной волны были в направлении магнитный колебания ЭМ волны. Но эксперименты Стокса не могли не обнаружить электрический вибрации, потому что они имеют большую склонность к взаимодействию с материей. Короче говоря, колебания МакКуллага-Неймана имели механический аналог, но колебания Френеля были теми, которые с большей вероятностью могли быть обнаружены в экспериментах.[Примечание 4]
Современная практика
Электромагнитная теория света еще больше подчеркнула электрический вибрации из-за их взаимодействия с веществом,[5] тогда как старая «плоскость поляризации» содержала магнитный векторов. Следовательно, электромагнитная теория укрепила бы соглашение о том, что колебания нормальны к плоскости поляризации - при условии, конечно, что человек был знаком с историческим определением плоскости поляризации. Но если на человека повлияли физические соображения один, то, как Фейнман[9] и Британика[4] Как показано, можно было бы обратить внимание на электрические векторы и предположить, что «плоскость» поляризации (если нужна такая концепция) содержала эти векторы.
Однако неясно, нужна ли вообще «плоскость поляризации»: зная, какие векторы поля задействованы, можно указать поляризацию, указав ориентацию определенного вектора, или, как Родившийся и Волк предложить, указав «плоскость вибрации» этого вектора.[5] Hecht также предпочитает термин плоскость вибрации (или, чаще, плоскость вибрации), которую он определяет как плоскость E и волновая нормаль в соответствии с рис. 1 выше.[29]
Остальные виды использования
В оптически хиральный среда - то есть та, в которой направление поляризации постепенно поворачивается по мере распространения волны - выбор определения «плоскости поляризации» не влияет на существование или направление («направленность») вращения. Это тот контекст, в котором двусмысленность термина плоскость поляризации больше не вызывает путаницы.[30]
Есть также контекст, в котором исходное определение может напрашиваться само собой. В немагнитном нехиральном кристалле двухосный класс (в котором нет обычного преломления, но оба преломления нарушают Закон Снеллиуса), есть три взаимно перпендикулярные плоскости, для которых скорость света изотропна внутри плоскости при условии, что электрические векторы перпендикулярны плоскости.[31] Эта ситуация, естественно, привлекает внимание к плоскости, перпендикулярной вибрациям, как это предполагал Френель, и эта плоскость действительно является плоскостью поляризации, как определено Френелем или Малусом.
Однако в большинстве случаев концепция «плоскости поляризации», отличной от плоскости, содержащей электрические «колебания», возможно, стала избыточной и, безусловно, стала источником путаницы. По словам Born & Wolf, «этот термин… лучше не использовать».[32]
Примечания
- ^ Этот вывод не следует, если среда оптически вращающийся (см., например, Darrigol, 2012, стр. 253n, 257n); однако в этой статье для существования стабильной плоскости поляризации необходимо отсутствие оптического вращения.
- ^ Угол отражения, при котором происходит это изменение, стал известен как Угол Брюстера, после экспериментального определения его зависимости от показателя преломления Дэвид Брюстер в 1815 г.
- ^ Фактическое написание этого трактата (Френель, 1822 г.) было очевидно завершено к середине 1821 г .; см. I. Grattan-Guinness, Свертки во французской математике, 1800–1840 гг., Базель: Birkhäuser, 1990, т. 2, стр. 884.
- ^ Относительно ограничений упруго-электромагнитных аналогий см., Например, Born & Wolf, 1970, pp. Xxiv – xxv; Дарригол, 2012, с. 227–32.
Рекомендации
- ^ а б J.G. Ланни и Д. Уир, «Все аспекты конической рефракции», Новости Europhysics, т. 37, нет. 3 (май – июнь 2006 г.), стр. 26–9, doi.org/10.1051/epn:2006305, at pp. 26–7.
- ^ а б Бухвальд, 1989, стр. 54.
- ^ Страттон, 1941, стр. 280; Born & Wolf, 1970, стр. 43, 681.
- ^ а б c М. Лунц (?) И др., «Двойное лучепреломление», Британская энциклопедия, по состоянию на 15 сентября 2017 г.
- ^ а б c Born & Wolf, 1970, стр. 28.
- ^ а б Френель, 1827, тр. Хобсон, стр. 318.
- ^ а б Френель, 1822, тр. Молодые, часть 7, п. 406.
- ^ Born & Wolf, 1970, стр. 28, 43.
- ^ а б Р. П. Фейнман, Р. Б. Лейтон и М. Сэндс, Лекции Фейнмана по физике, Калифорнийский технологический институт, 1963–2013, томя, Лекция 33.
- ^ а б c Страттон, 1941, стр. 280.
- ^ Born & Wolf, 1970, стр. 668.
- ^ Гюйгенс, 1690, тр. Томпсон, стр. 92–4.
- ^ Гюйгенс, 1690, тр. Томпсон, стр. 55–6.
- ^ Бухвальд, 1989, стр. 31–43; Дарригол, 2012, с. 191–2.
- ^ Бухвальд, 1989, стр. 45.
- ^ Born & Wolf, 1970, стр. 43, 681.
- ^ а б Merriam-Webster, Inc., «Плоскость поляризации», по состоянию на 15 сентября 2017 г.
- ^ Бухвальд, 1989, стр. 227–9.
- ^ Дарригол, 2012, с. 212.
- ^ Алдис, 1879, стр. 8–9.
- ^ Алдис, 1879, стр.9, 20.
- ^ Дарригол, 2012, с. 258–60.
- ^ Whittaker, 1910, стр. 127, 132–5.
- ^ Пауэлл, 1856, стр. 4–5; Whittaker, 1910, стр. 149.
- ^ а б Г.Г. Стокса, «К динамической теории дифракции» (читать 26 ноября 1849 г.), Труды Кембриджского философского общества, т. 9, часть 1 (1851), стр. 1–62, стр. 4–5.
- ^ Пауэлл, 1856, стр. 19–20; Whittaker, 1910, стр. 168–9.
- ^ Whittaker, 1910, стр. 169–70.
- ^ Дж. М. Карчоне и Ф. Каваллини, «Об акустико-электромагнитной аналогии», Волновое движение, т. 21 (1995), стр. 149–62. (Обратите внимание, что аналогия авторов только двумерна.)
- ^ Hecht, 2017, стр. 338.
- ^ Действительно, это единственный контекст, в котором Хехт (5-е изд., 2017) использует термин плоскость поляризации (стр. 386, 392).
- ^ Ср. Дженкинс, Х. Белый, Основы оптики, 4-е изд., Нью-Йорк: McGraw-Hill, 1976, ISBN 0-07-032330-5, pp. 553–4, в том числе рис. 26я.
- ^ Born & Wolf, 1970, стр. 43.
Библиография
- W.S. Алдис, 1879 г., Глава о теории двойного лучепреломления Френеля, 2-е изд., Кембридж: Дейтон, Белл и Ко. / Лондон: Джордж Белл и сыновья.
- М. Борн и Э. Вольф, 1970 г., Принципы оптики, 4-е изд., Оксфорд: Pergamon Press.
- J.Z. Бухвальд, 1989 г., Возникновение волновой теории света: оптическая теория и эксперимент в начале девятнадцатого века, Издательство Чикагского университета, ISBN 0-226-07886-8.
- О. Дарригол, 2012, История оптики: от греческой античности до девятнадцатого века, Оксфорд, ISBN 978-0-19-964437-7.
- А. Френель, 1822 г., Де ла Люмьер (На свете), в J. Riffault (ed.), Дополнение à la traduction française de la cinquième édition du "Système de Chimie" par Th. Томсон, Париж: Chez Méquignon-Marvis, 1822, стр. 1–137, 535–9; перепечатано в Fresnel, 1866–70, vol. 2, стр. 3–146; перевод Т. Янга как «Элементарный взгляд на волновую теорию света», Ежеквартальный журнал науки, литературы и искусства, т. 22 января - июн. 1827), стр.127–41, 441–54; т. 23 июля - декабря 1827), стр.113–35, 431–48; т. 24 января - июн. 1828), стр.198–215; т. 25 (июль - декабрь 1828), стр.168–91, 389–407; т. 26 (янв. - июн. 1829), стр.159–65.
- А. Френель, 1827, "Память о двойном преломлении", Mémoires de l'Académie Royale des Sciences de l'Institut de France, т.VII (за 1824 г., напечатано 1827 г.), стр. 45–176; переиздано как «Второй мемуар…» в Fresnel, 1866–70, vol. 2, стр. 479–596; перевод А.В. Хобсон как «Воспоминания о двойном лучепреломлении», в Р. Тейлоре (ред.), Научные воспоминания, т.V (Лондон: Тейлор и Фрэнсис, 1852 г.), стр. 238–333. (Приведенные номера страниц взяты из перевода.)
- А. Френель (ред. Х. де Сенармон, Э. Верде и Л. Френель), 1866–70, Совершенные произведения Августина Френеля (3 тома), Париж: Imprimerie Impériale; т. 1 (1866), т. 2 (1868), т. 3 (1870).
- Э. Хехт, 2017, Оптика, 5-е изд., Pearson Education, ISBN 978-1-292-09693-3.
- К. Гюйгенс, 1690, Traité de la Lumière (Лейден: Ван дер Аа), переведенный С.П. Томпсоном как Трактат о свете, University of Chicago Press, 1912; Project Gutenberg, 2005. (Указанные номера страниц соответствуют изданию 1912 года и изданию Gutenberg HTML.)
- Б. Пауэлл (июль 1856 г.), «О демонстрации формул Френеля для отраженного и преломленного света и их применениях», Философский журнал и Научный журнал, Серия 4, т. 12, вып. 76. С. 1–20.
- J.A. Страттон, 1941 г., Электромагнитная теория, Нью-Йорк: Макгроу-Хилл.
- Э. Т. Уиттакер, 1910, История теорий эфира и электричества: от эпохи Декарта до конца девятнадцатого века, Лондон: Longmans, Green, & Co.



