WikiDer > Политроп

Нормированная плотность как функция длины шкалы для широкого диапазона показателей политропы

В астрофизика, а политроп относится к решению Уравнение Лейна – Эмдена в которой давление зависит от плотность в виде

${ Displaystyle Р = К ро ^ {(п + 1) / п},}$

куда п давление, ρ это плотность и K это постоянный из соразмерность.^[1] Постоянная п известен как индекс политропы; обратите внимание, однако, что политропный индекс имеет альтернативное определение, как с п как показатель степени.

Это отношение не следует интерпретировать как уравнение состояния, в котором говорится п как функция как ρ, так и Т (в температура); однако в частном случае, описанном уравнением политропы, существуют другие дополнительные отношения между этими тремя величинами, которые вместе определяют уравнение. Таким образом, это просто соотношение, которое выражает предположение об изменении давления с радиус в терминах изменения плотности с радиусом, что дает решение уравнения Лейна – Эмдена.

Иногда слово политроп может относиться к уравнению состояния, которое похоже на термодинамический отношение выше, хотя это потенциально сбивает с толку, и его следует избегать. Желательно ссылаться на жидкость сам (в отличие от решения уравнения Лейна – Эмдена) как политропная жидкость. Уравнение состояния политропной жидкости достаточно общее, чтобы такие идеализированные жидкости находили широкое применение за пределами ограниченной проблемы политропов.

Показатель политропы (политропы) эквивалентен давлению производная из объемный модуль ^[2] где его отношение к Уравнение состояния Мурнагана также был продемонстрирован. Следовательно, соотношение политроп лучше всего подходит для относительно низкого давления (ниже 10⁷ Па) и высокого давления (более 10¹⁴ Па) условия, при которых производная по давлению модуля объемной упругости, эквивалентная индексу политропы, почти постоянна.

Примеры моделей по индексу политропы

Плотность (нормализованная к средней плотности) в зависимости от радиуса (нормализованная по внешнему радиусу) для политропа с индексом n = 3.

• Индекс п = 0 политроп часто используется для моделирования скалистые планеты также.^{[Почему?]}
• Нейтронные звезды хорошо смоделированный политропами с индексом между п = 0.5 и п = 1.
• Политроп с индексом п = 1.5 хорошая модель для полностью конвективного звездные ядра^[3][4](как у красные гиганты), коричневые карлики, гигантские газообразные планеты (подобно Юпитер). С этим индексом показатель политропы равен 5/3, что является коэффициент теплоемкости (γ) для одноатомный газ. Для внутренней части газовых звезд (состоящих из ионизированный водород или же гелий), это следует из идеальный газ приближение для естественная конвекция условия.
• Политроп с индексом п = 1.5 также хорошая модель для белые карлики малой массы, согласно уравнение состояния не-релятивистский дегенеративная материя.^[5]
• Политроп с индексом п = 3 является хорошей моделью для ядер белых карликов более высоких масс согласно уравнению состояния релятивистский дегенеративная материя.^[5]
• Политроп с индексом п = 3 обычно также используется для моделирования главная последовательность звезды как наш солнце, по крайней мере, в зона излучения, соответствующий Стандартная модель Эддингтона из звездная структура.^[6]
• Политроп с индексом п = 5 имеет бесконечный радиус. Это соответствует простейшей правдоподобной модели самосогласованной звездной системы, впервые изученной Артур Шустер в 1883 г., и точное решение.
• Политроп с индексом п = ∞ соответствует тому, что называется изотермический шар, это изотермический самогравитирующий шар газа, структура которого идентична структуре бесстолкновительной системы звезд типа шаровое скопление. Это связано с тем, что для идеального газа температура пропорциональна ρ^{1 / п}так бесконечно п соответствует постоянной температуре.

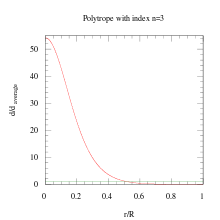
Как правило, по мере увеличения показателя политропы распределение плотности более сильно взвешивается к центру (р = 0) тела.

Рекомендации

Смотрите также

• Политропный процесс
• Уравнение состояния
• Уравнение состояния Мурнагана