WikiDer > ProbOnto
| ProbOnto | |
|---|---|
 | |
| Ключевые слова | Статистика, Распределение вероятностей |
| Цель | Разработка, внедрение и поддержка базы знаний и онтологии распределений вероятностей. |
| Продолжительность | 2015 – |
| Интернет сайт | пробонто |
ProbOnto это база знаний и онтология из распределения вероятностей.[1][2] ProbOnto 2.5 (выпущен 16 января 2017 г.) содержит более 150 уни- и многомерные распределения и альтернативные параметризации, более 220 взаимосвязей и формул повторной параметризации, поддерживающие также кодирование эмпирических и одномерных распределение смеси.
Вступление
ProbOnto изначально был разработан для облегчения кодирования нелинейно-смешанные модели эффектов и их аннотации на языке разметки Pharmacometrics Markup Language (PharmML)[3][4] разработан DDMoRe,[5][6] ан Инициатива по инновационным лекарствам проект. Однако ProbOnto, благодаря своей общей структуре, может применяться на других платформах и в инструментах моделирования для кодирования и аннотирования различных моделей, применимых к дискретным (например, считать, категоричный и время до события) и непрерывные данные.
База знаний
База знаний хранит для каждого распределения:
- Плотность вероятности или же масса функции и где доступно кумулятивное распределение, опасность и выживание функции.
- Связанные величины, такие как среднее значение, медиана, мода и дисперсия.
- Параметр и поддерживать/ определения диапазона и тип распределения.
- Латекс и р код для математических функций.
- Определение модели и ссылки.
Отношения
ProbOnto хранит в версии 2.5 более 220 взаимосвязей между одномерными распределениями с повторной параметризацией в качестве особого случая, см. Рисунок. Хотя в литературе этой формой отношений часто пренебрегают, и авторы концентрируют одну конкретную форму для каждого распределения, они имеют решающее значение с точки зрения совместимости. ProbOnto фокусируется на этом аспекте и предлагает более 15 дистрибутивов с альтернативными параметризациями.
Альтернативные параметризации
Многие распределения определяются с помощью математически эквивалентных, но алгебраически различных формул. Это приводит к проблемам при обмене моделями между программными инструментами.[7] Следующие примеры иллюстрируют это.
Нормальное распределение
Нормальное распределение можно определить как минимум тремя способами
- Normal1 (μ, σ) с иметь в виду, μ и стандартное отклонение, σ [8]
- Normal2 (μ, υ) со средним, μ и отклонение, υ = σ ^ 2[9] или же
Формулы повторной параметризации
Следующие формулы можно использовать для повторного расчета трех различных форм нормального распределения (мы используем сокращения, т.е. вместо так далее.)
Логнормальное распределение
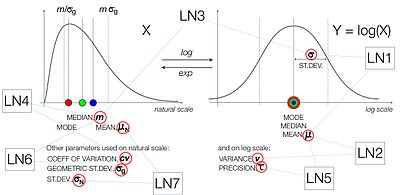
В случае логнормальное распределение есть еще варианты. Это связано с тем, что его можно параметризовать с точки зрения параметров в натуральном и логарифмическом масштабе, см. Рисунок.
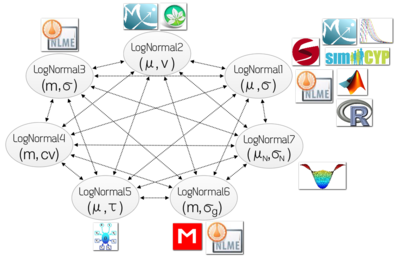
Доступные формы в ProbOnto 2.0:
- LogNormal1 (μ, σ) со средним значением μ и стандартным отклонением σ, оба в логарифмической шкале[8]
- LogNormal2 (μ, υ) со средним значением μ и дисперсией υ, оба в логарифмической шкале
- LogNormal3 (m, σ) с медиана, м, в натуральном масштабе и стандартное отклонение, σ, в логарифмической шкале.[8]
- LogNormal4 (m, cv) с медианой, m и коэффициент вариации, cv, как в натуральном масштабе
- LogNormal5 (μ, τ) со средним значением μ и точностью τ, оба в логарифмическом масштабе[12]
- LogNormal6 (m, σграмм) с медианой, m и геометрическое стандартное отклонение, σграмм, как в натуральном масштабе[13]
- LogNormal7 (μN, σN) со средним, μN, и стандартное отклонение σN, как в натуральном масштабе[14]
База знаний ProbOnto хранит такие формулы повторной параметризации, чтобы обеспечить правильный перевод моделей между инструментами.
Примеры повторной параметризации
Рассмотрим ситуацию, когда нужно запустить модель, используя два разных инструмента оптимального проектирования, например ПФИМ[15] и PopED.[16] Первый поддерживает LN2, второй - параметризацию LN7 соответственно. Следовательно, требуется повторная параметризация, иначе два инструмента дадут разные результаты.
Для перехода следующие формулы верны.
Для перехода следующие формулы верны.
Все остальные формулы повторной параметризации можно найти в документе спецификации на веб-сайте проекта.[2]
Онтология
База знаний построена на основе простой онтологической модели. По своей сути вероятностное распределение является экземпляром своего класса, специализацией класса математических объектов. Распределение относится к ряду других индивидов, которые являются экземплярами различных категорий в онтологии. Например, это параметры и связанные функции, связанные с заданным распределением вероятностей. Эта стратегия позволяет богатое представление атрибутов и отношений между объектами предметной области. Онтологию можно рассматривать как концептуальную схему в области математики и реализовывать в виде базы знаний PowerLoom.[17] Версия OWL создается программно с использованием Jena API.[18]
Выходные данные для ProbOnto предоставляются в виде дополнительных материалов и публикуются на веб-сайте probonto.org или связаны с ним. Версия ProbOnto для OWL доступна через службу поиска в онтологии (OLS).[19] для облегчения простого поиска и визуализации содержимого. Кроме того, OLS API предоставляет методы для программного доступа к ProbOnto и его интеграции в приложения. ProbOnto также зарегистрирован на портале BioSharing.[20]
Пробонто в PharmML
Интерфейс PharmML предоставляется в виде общей схемы XML для определения распределений и их параметров. Определение функций, таких как функция плотности вероятности (PDF), функция вероятности-массы (PMF), функция риска (HF) и функция выживания (SF), можно получить с помощью методов, представленных в схеме PharmML.
Пример использования
В этом примере показано, как кодируется распределение Пуассона с нулевым раздутием с помощью его кодовое название и декларируя это из своих параметров («rate» и «вероятностьOfZero»). Параметры модели Лямбда и P0 присваиваются кодовым именам параметров.
<Distribution> имя ="ZeroInflatedPoisson1"> имя ="ставка"> <ct:Assign> SymbIdRef =«Лямбда» /> </ct:Assign> </po:Parameter> имя ="вероятностьOfZero"> <ct:Assign> SymbIdRef =«P0» /> </ct:Assign> </po:Parameter> </po:ProbOnto></Distribution> Чтобы однозначно указать любой данный дистрибутив с помощью ProbOnto, достаточно указать его кодовое имя и кодовые имена его параметров. Дополнительные примеры и подробную спецификацию можно найти на сайте проекта.[2]
Смотрите также
- Список вероятностных распределений
- Онтология (информация_наука)
- Связи между распределениями вероятностей
- Язык веб-онтологий
Рекомендации
- ^ Сват, MJ; Grenon, P; Вималаратне, S (2016). «ПробОнто: онтология и база знаний вероятностных распределений». Биоинформатика. 32: 2719. Дои:10.1093 / биоинформатика / btw170. ЧВК 5013898. PMID 27153608.
- ^ а б c Главный сайт проекта, URL: http://probonto.org
- ^ Сват MJ. и другие. (2015). Язык разметки фармакометрии (PharmML): открытие новых перспектив для обмена моделями при разработке лекарств. CPT Pharmacometrics Syst Pharmacol, 4 (6): 316-9.
- ^ Веб-сайт PharmML, URL: http://pharmml.org
- ^ Сайт проекта DDMoRe, URL: http://ddmore.eu
- ^ Описание ProbOnto на сайте DDMoRe, URL: http://ddmore.eu/probonto
- ^ LeBauer DS et al. Перевод функций плотности вероятности: от R к BUGS и обратно, R Journal, 2013
- ^ а б c Forbes et al. Распределения вероятностей (2011), John Wiley & Sons, Inc.
- ^ Wolfram Mathworld, URL: http://mathworld.wolfram.com/NormalDistribution.html
- ^ Пакет R 'LaplacesDemon', URL: http://search.r-project.org/library/LaplacesDemon/html/dist.Normal.Precision.html
- ^ Сайерт Р.М., М.Х. ДеГрут, Байесовский анализ и неопределенность в экономике (1987), Теория Роуман и Литтлфилд
- ^ Ланн, Д. (2012). Книга BUGS: практическое введение в байесовский анализ. Тексты инстатистической науки. CRC Press.
- ^ Лимперт, Э., Стахел, В. А., и Эббт, М. (2001). Логнормальные распределения в науках: ключи и подсказки. BioScience, 51 (5): 341-352.
- ^ Nyberg J. et al. (2012) PopED - расширенный, распараллеленный инструмент для оптимального проектирования населения. Компьютерные методы Программы Biomed .; 108 (2): 789-805. DOI: 10.1016 / j.cmpb.2012.05.005
- ^ Retout S, Duffull S, Mentré F (2001) Разработка и внедрение популяционной информационной матрицы Фишера для оценки популяционных фармакокинетических дизайнов. Comp Meth Pro Biomed 65: 141–151
- ^ Команда разработчиков PopED (2016). Руководство по PopED, версия 2.13. Технический отчет, Уппсальский университет.
- ^ MacGregor R. et al. (1997) Руководство по Powerloom. ISI, Университет Южной Калифорнии, Марина-дель-Рей.
- ^ Макбрайд Б. (2001) Йена: Реализация модели RDF и спецификации синтаксиса. В: SemWeb.
- ^ ProbOnto в службе поиска онтологий, URL: http://www.ebi.ac.uk/ols/ontologies/probonto
- ^ ProbOnto на BioSharing, базе биологических баз данных, URL: https://biosharing.org/biodbcore-000772
внешняя ссылка
- Сайт ProbOnto
- Диаграмма Лемиса
- Окончательный обозреватель одномерного распределения вероятностей - скорее всего, самая большая бесплатная коллекция одномерных дистрибутивов и их функций.
- UncertML

![{ displaystyle P (x; { boldsymbol { mu}}, { boldsymbol { sigma}}) = { frac {1} { sigma { sqrt {2 pi}}}} exp { Большой [} - { frac {(x- mu) ^ {2}} {2 sigma ^ {2}}} { Big]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ee9c05d4a6445f3697d67a92a282c13df0beb90)
![{ displaystyle P (x; { boldsymbol { mu}}, { boldsymbol {v}}) = { frac {1} {{ sqrt {v}} { sqrt {2 pi}}}} exp { Big [} - { frac {(x- mu) ^ {2}} {2v}} { Big]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6294655c5a8137251de9c61996d58ade53312cc6)
![{ displaystyle P (x; { boldsymbol { mu}}, { boldsymbol { tau}}) = { sqrt { frac { tau} {2 pi}}} { Big [} - { frac { tau} {2}} (x- mu) ^ {2} { Big]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9245a601a57e2053f4e1e95894551a5830d3d175)





![{ displaystyle P (x; { boldsymbol { mu}}, { boldsymbol { sigma}}) = { frac {1} {x sigma { sqrt {2 pi}}}} exp { Big [} { frac {- ( log x- mu) ^ {2}} {2 sigma ^ {2}}} { Big]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2203c6532a8f2fb656f5d094facaa68c1d71da6)
![{ displaystyle P (x; { boldsymbol { mu}}, { boldsymbol {v}}) = { frac {1} {x { sqrt {v}} { sqrt {2 pi}}} } exp { Big [} { frac {- ( log x- mu) ^ {2}} {2v}} { Big]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70707ef688d2544dd7177b97b28c009935010536)
![{ displaystyle P (x; { boldsymbol {m}}, { boldsymbol { sigma}}) = { frac {1} {x sigma { sqrt {2 pi}}}} exp { Большой [} { frac {- [ log (x / m)] ^ {2}} {2 sigma ^ {2}}} { Big]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d066a6571c7ae5e27583711fc86d687d9deaef35)
![{ displaystyle P (x; { boldsymbol {m}}, { boldsymbol {cv}}) = { frac {1} {x { sqrt { log (cv ^ {2} +1)}} { sqrt {2 pi}}}} exp { Big [} { frac {- [ log (x / m)] ^ {2}} {2 log (cv ^ {2} +1)} }{Большой ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e62d3a100a18af22f94f3d47307e0b170994cd2c)
![{ displaystyle P (x; { boldsymbol { mu}}, { boldsymbol { tau}}) = { sqrt { frac { tau} {2 pi}}} { frac {1} { x}} exp { Big [} {- { frac { tau} {2}} ( log x- mu) ^ {2}} { Big]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/754af28c18e6d700d524fca45427c1df19ffeaf5)
![{ displaystyle P (x; { boldsymbol {m}}, { boldsymbol { sigma _ {g}}}) = { frac {1} {x log ( sigma _ {g}) { sqrt {2 pi}}}} exp { Big [} { frac {- [ log (x / m)] ^ {2}} {2 log ^ {2} ( sigma _ {g}) }}{Большой ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6f421a0dce7d8e99c7a9318b73317c5cd1ea362)
![{ displaystyle P (x; { boldsymbol { mu _ {N}}}, { boldsymbol { sigma _ {N}}}) = { frac {1} {x { sqrt {2 pi log { Big (} 1+ sigma _ {N} ^ {2} / mu _ {N} ^ {2} { Big)}}}}} exp { Bigg (} { frac {- { Big [} log (x) - log { Big (} { frac { mu _ {N}} { sqrt {1+ sigma _ {N} ^ {2} / mu _ { N} ^ {2}}}} { Big)} { Big]} ^ {2}} {2 log { Big (} 1+ sigma _ {N} ^ {2} / mu _ { N} ^ {2} { Big)}}} { Bigg)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96cda4673155da96615dcb0b7390b0d36d23fb25)



