WikiDer > Метод Ромберга - Википедия

В числовой анализ, Метод Ромберга (Ромберг 1955) используется для оценки определенный интеграл

${ displaystyle int _ {a} ^ {b} f (x) , dx}$

применяя Экстраполяция Ричардсона (Ричардсон 1911) неоднократно на правило трапеции или правило прямоугольника (правило средней точки). Оценки дают треугольная решетка. Метод Ромберга - это Формула Ньютона – Котеса - он вычисляет подынтегральное выражение в точках, расположенных на одинаковом расстоянии. Подынтегральное выражение должно иметь непрерывные производные, хотя неплохие результаты могут быть получены, если существует только несколько производных. Если возможно вычислить подынтегральное выражение в точках, разнесенных на неравные расстояния, тогда используйте другие методы, такие как Квадратура Гаусса и Квадратура Кленшоу – Кертиса обычно более точны.

Метод назван в честь Вернер Ромберг (1909–2003), которые опубликовали метод в 1955 году.

Метод

С помощью

${ displaystyle h_ {n} = { tfrac {1} {2 ^ {n}}} (b-a)}$

метод может быть индуктивно определен как

${ Displaystyle R (0,0) = h_ {1} (f (a) + f (b))}$

${ Displaystyle R (n, 0) = { tfrac {1} {2}} R (n-1,0) + h_ {n} sum _ {k = 1} ^ {2 ^ {n-1} } f (a + (2k-1) h_ {n})}$

${ Displaystyle R (n, m) = R (n, m-1) + { tfrac {1} {4 ^ {m} -1}} (R (n, m-1) -R (n-1) , м-1))}$

или же

${ Displaystyle R (n, m) = { tfrac {1} {4 ^ {m} -1}} (4 ^ {m} R (n, m-1) -R (n-1, m-1) ))}$

куда ${ Displaystyle п geq м ,}$ и ${ Displaystyle м geq 1 ,}$. В нотация большой O, ошибка для р(п, м) является (Мысовских 2002):

${ displaystyle O left (h_ {n} ^ {2m + 2} right). ,}$

Нулевая экстраполяция, р(п, 0), эквивалентно трапеция с 2^п + 1 балл; первая экстраполяция, р(п, 1), эквивалентно Правило Симпсона с 2^п +1 балл. Вторая экстраполяция, р(п, 2), эквивалентно Правило Буля с 2^п +1 балл. Дальнейшие экстраполяции отличаются от формул Ньютона-Котеса. В частности, дальнейшие экстраполяции Ромберга очень незначительно расширяют правило Буля, изменяя веса в отношения, аналогичные тем, которые используются в правиле Буля. Напротив, дальнейшие методы Ньютона-Котеса дают все более разные веса, что в конечном итоге приводит к большим положительным и отрицательным весам. Это свидетельствует о том, что методы полинома Ньютона-Котеса с большой степенью интерполяции не могут сходиться для многих интегралов, в то время как интегрирование Ромберга более стабильно.

Когда оценки функций дороги, может быть предпочтительнее заменить полиномиальную интерполяцию Ричардсона рациональной интерполяцией, предложенной Булирш и Стоер (1967).

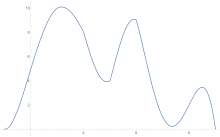
Геометрический пример

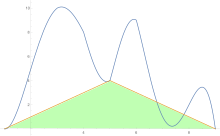
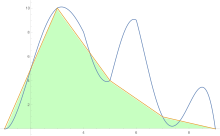
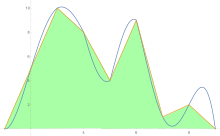
Чтобы оценить площадь под кривой, правило трапеций применяется сначала к цельному элементу, затем к двум, затем к четырем и так далее.

Один кусочек. Обратите внимание, поскольку оно начинается и заканчивается на нуле, это приближение дает нулевую площадь.

Два куска

Из четырех частей

Восемь частей

После получения оценок по правилу трапеций Экстраполяция Ричардсона применяется.

• Для первой итерации в формуле используются двухчастные и однократные оценки (4 × (более точный) - (менее точный)) / 3 Затем та же формула используется для сравнения оценки из четырех и двух частей, а также для более высоких оценок.
• Для второй итерации значения первой итерации используются в формуле (16 (более точный) - менее точный)) / 15
• Третья итерация использует следующую степень 4: (64 (более точно) - менее точно)) / 63 от значений, полученных на второй итерации.
• Схема продолжается до тех пор, пока не будет одна оценка.

• MA означает более точный, LA означает менее точный

Пример

Например, Функция Гаусса интегрируется от 0 до 1, т.е. функция ошибки erf (1) ≈ 0,842700792949715. Треугольный массив вычисляется построчно, и вычисление прекращается, если две последние записи в последней строке отличаются менее чем на 10.⁻⁸.

 0.77174333 0.82526296  0.84310283 0.83836778  0.84273605  0.84271160 0.84161922  0.84270304  0.84270083  0.84270066 0.84243051  0.84270093  0.84270079  0.84270079  0.84270079

Результат в правом нижнем углу треугольного массива соответствует показанным цифрам. Примечательно, что этот результат получен из менее точных приближений, полученных с помощью правила трапеции в первом столбце треугольного массива.

Выполнение

Вот пример компьютерной реализации метода Ромберга (в Язык программирования C).

#включают <stdio.h>#включают <math.h>пустотаdump_row(size_t я, двойной *р) {   printf("R [% 2zu] =", я);   за (size_t j = 0; j <= я; ++j){      printf("% f", р[j]);   }   printf(" п");}двойнойRomberg(двойной (*ж/ * функция для интеграции * /)(двойной), двойной /*Нижний предел*/ а, двойной /*верхний предел*/ б, size_t max_steps, двойной / * желаемая точность * / соотв) {   двойной R1[max_steps], R2[max_steps]; // буферы   двойной *Rp = &R1[0], *Rc = &R2[0]; // Rp - предыдущая строка, Rc - текущая строка   двойной час = (б-а); //размер шага   Rp[0] = (ж(а) + ж(б))*час*.5; // первый шаг трапеции   dump_row(0, Rp);   за (size_t я = 1; я < max_steps; ++я) {      час /= 2.;      двойной c = 0;      size_t ep = 1 << (я-1); // 2 ^ (n-1)      за (size_t j = 1; j <= ep; ++j) {         c += ж(а+(2*j-1)*час);      }      Rc[0] = час*c + .5*Rp[0]; // R (i, 0)      за (size_t j = 1; j <= я; ++j) {         двойной н_к = пау(4, j);         Rc[j] = (н_к*Rc[j-1] - Rp[j-1])/(н_к-1); // вычисляем R (i, j)      }      // Дамп i-го столбца R, R [i, i] - лучшая оценка на данный момент      dump_row(я, Rc);      если (я > 1 && фабрики(Rp[я-1]-Rc[я]) < соотв) {         возвращаться Rc[я-1];      }      // меняем местами Rn и Rc, так как нам нужна только последняя строка      двойной *rt = Rp;      Rp = Rc;      Rc = rt;   }   возвращаться Rp[max_steps-1]; // возвращаем наше лучшее предположение}

Рекомендации

• Ричардсон, Л. Ф. (1911), "Приближенное арифметическое решение конечными разностями физических задач, связанных с дифференциальными уравнениями, с приложением к напряжениям в каменной дамбе", Философские труды Королевского общества A, 210 (459–470): 307–357, Дои:10.1098 / рста.1911.0009, JSTOR 90994
• Ромберг, В. (1955), "Vereinfachte numerische Integration", Det Kongelige Norske Videnskabers Selskab Forhandlinger, Тронхейм, 28 (7): 30–36
• Тэчер-младший, Генри К. (июль 1964 г.), «Замечание по алгоритму 60: интеграция Ромберга», Коммуникации ACM, 7 (7): 420–421, Дои:10.1145/364520.364542
• Bauer, F.L .; Rutishauser, H .; Штифель, Э. (1963), Метрополис, Северная Каролина; и другие. (ред.), "Новые аспекты в числовой квадратуре", Экспериментальная арифметика, высокоскоростные вычисления и математика, Труды симпозиумов по прикладной математике, AMS (15): 199–218
• Булирш, Роланд; Стоер, Йозеф (1967), "Серия справочников" Численное интегрирование. Численные квадратуры путем экстраполяции ", Numerische Mathematik, 9: 271–278, Дои:10.1007 / bf02162420
• Мысовских, И. (2002), «Метод Ромберга», в Hazewinkel, Michiel (ed.), Энциклопедия математики, Springer-Verlag, ISBN 1-4020-0609-8
• Нажмите, WH; Теукольский С.А.; Феттерлинг, штат Вашингтон; Фланнери, BP (2007), «Раздел 4.3. Интеграция Ромберга», Числовые рецепты: искусство научных вычислений (3-е изд.), Нью-Йорк: Издательство Кембриджского университета, ISBN 978-0-521-88068-8

внешняя ссылка

• ROMBINT - код для MATLAB (автор: Мартин Каценак)
• Бесплатный онлайн-инструмент интеграции с использованием методов Ромберга, Фокса – Ромберга, Гаусса – Лежандра и других численных методов.
• SciPy реализация метода Ромберга