WikiDer > Стандартный шаговый метод

В стандартный шаговый метод (СТМ) представляет собой вычислительную технику, используемую для оценки одномерных профилей поверхностных вод в открытых каналах с постепенно изменяющимся потоком в установившихся условиях. Он использует комбинацию уравнений энергии, импульса и неразрывности для определения глубины воды с заданным уклоном трения. ${ displaystyle (S_ {f})}$, уклон канала ${ displaystyle (S_ {0})}$, геометрия канала, а также заданный расход. На практике этот метод широко используется в компьютерной программе. HEC-RAS, разработанный Инженерным гидрологическим инженерным центром армии США (HEC).^[1]

Основы потока в открытом канале

Рисунок 1. Концептуальный рисунок, используемый для определения терминов в уравнении энергии.^[2]

Фигура 2. Диаграмма, показывающая зависимость глубины потока (y) и полной энергии (E) для данного потока (Q). Обратите внимание на расположение критического потока, докритического потока и сверхкритического потока.

Уравнение энергии, используемое для поток в открытом канале вычисления являются упрощением уравнения Бернулли (см. Принцип Бернулли), который учитывает напор, вертикальный и скоростной напор. (Обратите внимание, что энергия и голова являются синонимами в гидродинамике. См. Напор для более подробной информации.) В открытых каналах предполагается, что изменения атмосферного давления незначительны, поэтому термин «напор», используемый в уравнении Бернулли, исключен. Полученное уравнение энергии показано ниже:

${ displaystyle H = z + y + { frac {v ^ {2}} {2g}}}$            Уравнение 1

Для заданного расхода и геометрии канала существует взаимосвязь между глубиной потока и полной энергией. Это показано ниже на графике зависимости энергии от глубины потока, широко известной как диаграмма E-y. На этом графике глубина минимума энергии известна как критическая глубина. Следовательно, эта глубина соответствует Число Фруда ${ displaystyle (F_ {n})}$ из 1. Глубины, превышающие критическую, считаются «подкритическими» и имеют число Фруда меньше 1, в то время как глубины меньше критической глубины считаются сверхкритическими и имеют числа Фруда больше 1. (Подробнее см. Безразмерные диаграммы удельной энергии для потока в открытом канале.)

${ displaystyle F_ {n} = { frac {v} {(g { frac {A} {B}}) ^ {0.5}}}}$           Уравнение 2

В условиях установившегося режима потока (например, при отсутствии волны наводнения) поток в открытом канале можно разделить на три типа потока: равномерный поток, постепенно меняющийся поток и быстро меняющийся поток. Равномерное течение описывает ситуацию, когда глубина потока не изменяется с расстоянием вдоль канала. Это может происходить только в гладком канале, в котором не происходит никаких изменений потока, геометрии канала, шероховатости или наклона канала. Во время равномерного потока глубина потока называется нормальной глубиной (yn). Эта глубина аналогична предельной скорости объекта при свободном падении, где силы тяжести и трения находятся в равновесии (Моглен, 2013).^[3] Обычно эта глубина рассчитывается с использованием Формула укомплектования. Постепенно изменяющийся поток возникает, когда изменение глубины потока при изменении расстояния потока очень мало. В этом случае все еще применяются гидростатические соотношения, разработанные для равномерного потока. Примеры этого включают подпор за сооружением в потоке (например, плотина, шлюз, плотина и т. Д.), Когда в русле есть сужение и когда есть небольшое изменение уклона русла. Быстро меняющийся поток возникает, когда изменение глубины потока при изменении расстояния потока значительно. В этом случае гидростатические соотношения не подходят для аналитических решений, и необходимо использовать непрерывность количества движения. Примеры этого включают большие изменения наклона, такие как водосброс, резкое сужение / расширение потока или гидравлический скачок.

Профили водной поверхности (постепенно меняющийся поток)

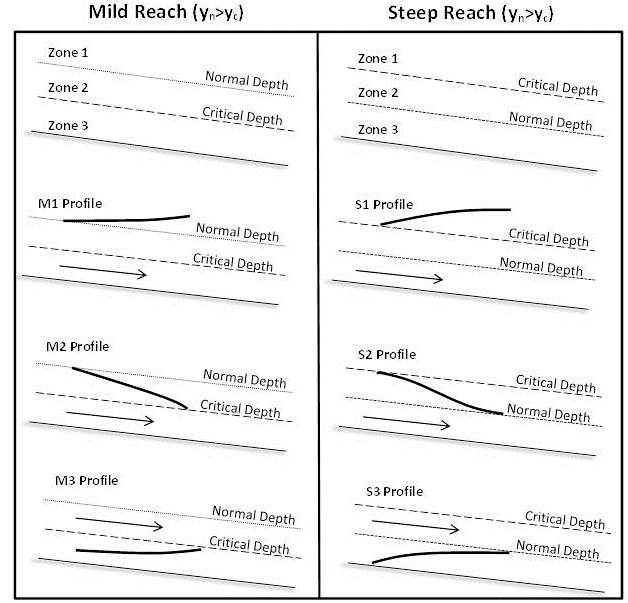
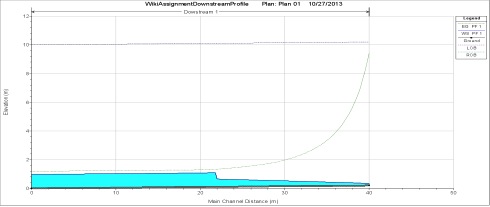
Как правило, STM используется для построения «профилей поверхностных вод» или продольных представлений глубины канала для каналов, в которых поток постепенно изменяется. Эти переходы можно классифицировать по условию досягаемости (мягкий или крутой), а также по типу выполняемого перехода. Мягкие участки встречаются там, где нормальная глубина является докритической (yn> yc), а крутые - там, где нормальная глубина является сверхкритической (yn

Рисунок 3. На этом рисунке показаны различные классы профилей поверхностных вод на крутых и пологих участках при постепенно меняющихся условиях потока.^[4] Примечание. Столбец Steep Reach должен иметь пометку «Steep Reach (yn

Приведенные выше профили поверхностных вод основаны на основном уравнении для постепенно изменяющегося потока (см. Ниже).

${ displaystyle { frac {dy} {dx}} = { frac {S_ {0} -S_ {f}} {1-F_ {n} ^ {2}}}}$           Уравнение 3

Это уравнение (и соответствующие профили поверхностных вод) основано на следующих предположениях:

• Уклон относительно небольшой
• Поперечное сечение канала известно на интересующих станциях
• Распределение гидростатического давления

Расчет стандартным шаговым методом

STM численно решает уравнение 3 посредством итеративного процесса. Это может быть выполнено с использованием метода деления пополам или метода Ньютона-Рафсона, и по сути это решение для полного напора в указанном месте с использованием уравнений 4 и 5 путем изменения глубины в указанном месте.^[5]

${ displaystyle H_ {2} = H_ {1} -h_ {f}}$           Уравнение 4

${ displaystyle H_ {2} = h_ {vel} + h_ {ele}}$           Уравнение 5

Чтобы использовать эту технику, важно отметить, что вы должны иметь некоторое представление о моделируемой системе. Для каждого постепенно изменяющегося перехода потока вы должны знать оба граничных условия и также должны рассчитать длину этого перехода. (Например, для профиля M1 вы должны найти подъем в граничном условии ниже по потоку, нормальную глубину в граничном условии выше по потоку, а также длину перехода.) Чтобы найти длину постепенно изменяющихся переходов потока, повторите операцию « длина шага ”вместо высоты на высоте граничного условия до тех пор, пока уравнения 4 и 5 не согласятся. (например, для профиля M1 положение 1 будет условием ниже по потоку, и вы должны решить для положения два, где высота равна нормальной глубине.)

Численный метод Ньютона – Рафсона.

Компьютерные программы, такие как excel, содержат функции итерации или поиска цели, которые могут автоматически вычислять фактическую глубину вместо итераций вручную.

Концептуальные профили поверхностных вод (шлюзовые ворота)

Рисунок 4. Иллюстрация профилей поверхностных вод, связанных со шлюзом на небольшом участке (вверху) и на крутом участке (внизу).

На рис. 4 показаны различные профили поверхностных вод, связанные со шлюзом на небольшом участке (вверху) и на крутом участке (внизу). Обратите внимание: затвор шлюза вызывает дросселирование в системе, вызывая профиль «подпора» прямо перед затвором. В легкой досягаемости гидравлический прыжок происходит за воротами, но на крутых склонах гидравлический скачок происходит перед воротами. Важно отметить, что постепенно меняющиеся уравнения потока и связанные с ними численные методы (включая стандартный шаговый метод) не могут точно моделировать динамику гидравлического скачка.^[6] Увидеть Гидравлические прыжки в прямоугольных каналах страницу для получения дополнительной информации. Ниже в примере задачи будут использоваться концептуальные модели для построения профиля поверхностных вод с помощью STM.

Пример проблемы

Решение

Используя рисунок 3, зная условия до и после затвора, а также значения глубины по обе стороны от затвора, можно получить общую оценку профилей до и после затвора. Выше по течению поверхность воды должна подниматься с нормальной глубины 0,97 м до 9,21 м у ворот. Единственный способ сделать это на небольшом досягаемости - следовать профилю M1. Та же логика применяется ниже по течению, чтобы определить, что поверхность воды следует профилю M3 от затвора до тех пор, пока глубина не достигнет сопряженной глубины нормальной глубины, в этот момент образуется гидравлический скачок, чтобы поднять поверхность воды до нормальной глубины.

Шаг 4: Используйте метод Ньютона-Рафсона для решения профилей поверхностных вод M1 и M3. Участки, расположенные выше и ниже по потоку, должны быть смоделированы отдельно с начальной глубиной 9,21 м для участка выше по потоку и 0,15 м для участка ниже по потоку. Глубину вниз по течению следует моделировать только до тех пор, пока она не достигнет сопряженной глубины нормальной глубины, в этот момент образуется гидравлический скачок. Представленное решение объясняет, как решить проблему в электронной таблице, показывая расчеты столбец за столбцом. В Excel функцию поиска цели можно использовать для установки в столбце 15 значения 0 путем изменения оценки глубины в столбце 2 вместо повторения вручную.

Таблица 1: Таблица метода Ньютона-Рафсона для расчета высоты водной поверхности ниже по течению

Шаг 5: Объедините результаты из разных профилей и отобразите.

Нормальная глубина была достигнута примерно на 2200 метров выше ворот.

Шаг 6: Решите проблему в среде моделирования HEC-RAS:

Объяснение тонкостей работы HEC-RAS выходит за рамки этой страницы в Википедии. Для тех, кто хочет узнать больше, руководство пользователя HEC-RAS является отличным учебным пособием, а программа является бесплатной для всех.

Первые два рисунка ниже - это профили водной поверхности вверх и вниз по течению, смоделированные HEC-RAS. Также представлена ​​таблица, в которой сравниваются различия между профилями, оцененными двумя разными методами на разных станциях, чтобы показать согласованность между двумя методами. В то время как два разных метода моделировали аналогичные формы водной поверхности, стандартный пошаговый метод предсказывал, что поток будет проходить большее расстояние, чтобы достичь нормальной глубины до и после затвора. Это растяжение вызвано ошибками, связанными с принятием средних градиентов между двумя интересующими станциями во время наших расчетов. Меньшие значения dx уменьшат эту ошибку и позволят получить более точные профили поверхности.

Модель HEC-RAS рассчитала, что вода поднимается до высоты 9,21 метра на верхней стороне шлюзового затвора, что совпадает с рассчитанным вручную значением. Нормальная глубина была достигнута на отметке около 1700 метров перед воротами.

HEC-RAS смоделировал гидравлический прыжок, который произошел на 18 метров ниже шлюзового затвора.

Рекомендации