WikiDer > Проблема Стокса

Задача Стокса в вязкой жидкости из-за гармонического колебания плоской жесткой пластины (нижний черный край). Скорость (синяя линия) и перемещение частиц (красные точки) в зависимости от расстояния до стены.

В гидродинамике Проблема Стокса также известный как Вторая проблема Стокса или иногда упоминается как Пограничный слой Стокса или же Колеблющийся пограничный слой - задача определения потока, создаваемого колеблющейся твердой поверхностью, названной в честь Сэр Джордж Стоукс. Это считается одной из простейших нестационарных задач, имеющих точное решение для Уравнения Навье-Стокса^[1][2]. В бурный поток, это все еще называют пограничным слоем Стокса, но теперь нужно полагаться на эксперименты, численное моделирование или же приблизительные методы чтобы получить полезную информацию о потоке.

Описание потока^[3][4]

Рассмотрим бесконечно длинную пластину, которая колеблется со скоростью ${ displaystyle U cos omega t}$ в ${ displaystyle x}$ направление, которое находится в ${ displaystyle y = 0}$ в бесконечной области жидкости, где ${ displaystyle omega}$ - частота колебаний. Несжимаемый Уравнения Навье-Стокса сократить до

${ displaystyle { frac { partial u} { partial t}} = nu { frac { partial ^ {2} u} { partial y ^ {2}}}}$

куда ${ displaystyle nu}$ это кинематическая вязкость. Градиент давления в проблему не входит. Начальный, условие противоскольжения на стене

${ Displaystyle и (0, T) = U соз omega t, quad и ( infty, t) = 0,}$

а второе граничное условие связано с тем, что движение при ${ displaystyle y = 0}$ не ощущается в бесконечности. Течение возникает только за счет движения пластины, градиент давления отсутствует.

Решение^[5][6]

Начальное условие не требуется из-за периодичности. Поскольку и уравнение, и граничные условия линейны, скорость может быть записана как действительная часть некоторой комплексной функции

${ Displaystyle и = U Re влево [е ^ {я омега т} е (у) вправо]}$

потому что ${ Displaystyle соз омега т = ре е ^ {я омега т}}$.

Подстановка этого в уравнение в частных производных сводит его к обыкновенному дифференциальному уравнению

${ displaystyle f '' - { frac {я omega} { nu}} f = 0}$

с граничными условиями

${ Displaystyle е (0) = 1, четырехъядерный е ( infty) = 0}$

Решение вышеуказанной проблемы

${ displaystyle f (y) = exp left [- { frac {1 + i} { sqrt {2}}} { sqrt { frac { omega} { nu}}} y right] }$

${ displaystyle u (y, t) = Ue ^ {- { sqrt { frac { omega} {2 nu}}} y} cos left ( omega t - { sqrt { frac { омега} {2 nu}}} у right)}$

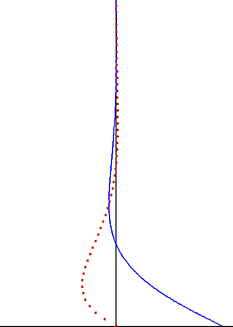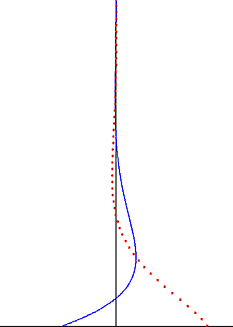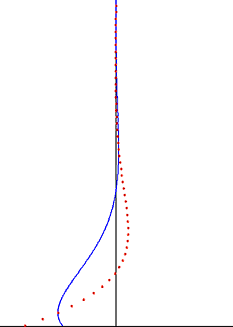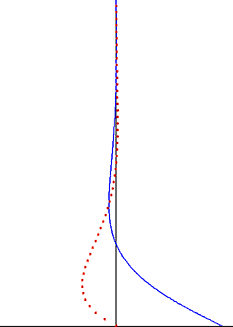
Возмущение, создаваемое колеблющейся пластиной, распространяется как поперечная волна через жидкость, но сильно затухает экспоненциальным множителем. Глубина проникновения ${ displaystyle delta = { sqrt {2 nu / omega}}}$ этой волны уменьшается с частотой колебаний, но увеличивается с кинематической вязкостью жидкости.

Сила на единицу площади, действующая на пластину жидкостью, равна

${ displaystyle F = mu left ({ frac { partial u} { partial y}} right) _ {y = 0} = { sqrt { rho omega mu}} U cos влево ( omega t - { frac { pi} {4}} right)}$

Между колебанием пластины и создаваемой силой существует фазовый сдвиг.

Колебания завихренности вблизи границы

Важное наблюдение из решения Стокса для осциллирующего потока Стокса состоит в том, что завихренность колебания приурочены к тонкому пограничному слою и затухают экспоненциально при отходе от стены.^[7] Это наблюдение справедливо и для случая турбулентного пограничного слоя. Вне пограничного слоя Стокса, который часто составляет основную часть объема жидкости, колебаниями завихренности можно пренебречь. В хорошем приближении колебания скорости потока равны безвихревый вне пограничного слоя, и потенциальный поток Теория применима к колебательной части движения. Это значительно упрощает решение этих проблем потока и часто применяется в областях безвихревого потока звуковые волны и волны на воде.

Жидкость ограничена верхней стенкой

Если область жидкости ограничена верхней неподвижной стенкой, расположенной на высоте ${ displaystyle y = h}$, скорость потока определяется выражением

${ Displaystyle и (Y, T) = { гидроразрыва {U} {2 ( cosh 2 lambda h- cos 2 lambda h)}} [e ^ {- lambda (y-2h)} cos ( omega t- lambda y) + e ^ { lambda (y-2h)} cos ( omega t + lambda y) -e ^ {- lambda y} cos ( omega t- lambda y +2 lambda h) -e ^ { lambda y} cos ( omega t + lambda y-2 lambda h)]}$

куда ${ displaystyle lambda = { sqrt { omega / (2 nu)}}}$.

Течение из-за колеблющегося градиента давления около плоской жесткой пластины

Пограничный слой Стокса из-за синусоидальный колебания скорости потока в дальней зоне. Горизонтальная скорость обозначена синей линией, а соответствующие горизонтальные отклонения частиц - красными точками.

Случай колеблющегося дальняя зона поток с пластиной, удерживаемой в состоянии покоя, может быть легко сконструирован из предыдущего решения для колеблющейся пластины, используя линейная суперпозиция решений. Рассмотрим равномерное колебание скорости ${ Displaystyle и ( infty, т) = U _ { infty} соз омега т}$ далеко от пластины и исчезающая скорость на пластине ${ displaystyle u (0, t) = 0}$. В отличие от неподвижной жидкости в исходной задаче, здесь градиент давления на бесконечности должен быть гармонической функцией времени. Тогда решение дается

${ displaystyle u (y, t) = U _ { infty} left [, cos omega t - { text {e}} ^ {- { sqrt { frac { omega} {2 nu }}} y} , cos left ( omega t - { sqrt { frac { omega} {2 nu}}} y right) right],}$

который равен нулю у стены г = 0, соответствующий условие противоскольжения для стены в состоянии покоя. Такая ситуация часто встречается в звуковые волны у твердой стены или для движения жидкости у морского дна в волны на воде. Завихренность колеблющегося потока у неподвижной стенки равна завихренности колеблющейся пластины, но противоположного знака.

Задача Стокса в цилиндрической геометрии

Крутильные колебания

Рассмотрим бесконечно длинный цилиндр радиуса ${ displaystyle a}$ проявляющие крутильные колебания с угловой скоростью ${ displaystyle Omega cos omega t}$ куда ${ displaystyle omega}$ это частота. Тогда после начальной переходной фазы скорость приближается к^[8]

${ displaystyle v _ { theta} = a Omega Re left [{ frac {K_ {1} (r { sqrt {i omega / nu}})} {K_ {1} (a { sqrt {i omega / nu}})}} e ^ {i omega t} right]}$

куда ${ displaystyle K_ {1}}$ - модифицированная функция Бесселя второго рода. Это решение может быть выражено реальным аргументом^[9] в качестве:

${ displaystyle { begin {align} v _ { theta} left (r, t right) & = Psi left lbrace left [{ textrm {kei}} _ {1} left ({ sqrt {R _ { omega}}} right) { textrm {kei}} _ {1} left ({ sqrt {R _ { omega}}} r right) + { textrm {ker}} _ {1} left ({ sqrt {R _ { omega}}} right) { textrm {ker}} _ {1} left ({ sqrt {R _ { omega}}} r right) right] cos left (t right) right. & + left. left [{ textrm {kei}} _ {1} left ({ sqrt {R _ { omega}}}} справа) { textrm {ker}} _ {1} left ({ sqrt {R _ { omega}}} r right) - { textrm {ker}} _ {1} left ({ sqrt { R _ { omega}}} right) { textrm {kei}} _ {1} left ({ sqrt {R _ { omega}}} r right) right] sin left (t right ) right rbrace конец {выровнено}}}$

куда

${ displaystyle Psi = left [{ textrm {kei}} _ {1} ^ {2} left ({ sqrt {R _ { omega}}} right) + { textrm {ker}} _ {1} ^ {2} left ({ sqrt {R _ { omega}}} right) right] ^ {- 1},}$

${ displaystyle mathrm {kei}}$ и ${ displaystyle mathrm {ker}}$ находятся Функции Кельвина и ${ displaystyle R _ { omega}}$к безразмерному колебательному числу Рейнольдса, определяемому как ${ displaystyle R _ { omega} = omega a ^ {2} / nu}$, существование ${ displaystyle nu}$ кинематическая вязкость.

Осевые колебания

Если цилиндр колеблется в осевом направлении со скоростью ${ displaystyle U cos omega t}$, то поле скорости равно

${ displaystyle u = U Re left [{ frac {K_ {0} (r { sqrt {i omega / nu}})} {K_ {0} (a { sqrt {i omega / nu}})}} e ^ {i omega t} right]}$

куда ${ displaystyle K_ {0}}$ - модифицированная функция Бесселя второго рода.

Поток Стокса-Куэтта^[10]

в Поток Куэтта, вместо поступательного движения одной из пластин будет выполняться колебание одной плоскости. Если у нас есть нижняя стенка в состоянии покоя на ${ displaystyle y = 0}$ и верхняя стена у ${ displaystyle y = h}$ совершает колебательное движение со скоростью ${ displaystyle U cos omega t}$, то поле скоростей определяется выражением

${ displaystyle u = U Re left {{ frac { sin ky} { sin kh}} right }, quad { text {where}} quad k = { frac {1 + i} { sqrt {2}}} { sqrt { frac { omega} { nu}}}.}$

Сила трения на единицу площади на движущейся плоскости равна ${ displaystyle - mu U Re {k cot kh }}$ а на неподвижной плоскости - ${ Displaystyle му U Re {к csc kh }}$.

Смотрите также

• Проблема Рэлея

Рекомендации