WikiDer > Порядок потоковой передачи

Stream order

В порядок потоков или порядок водоемов это положительное целое число используется в геоморфология и гидрология для обозначения уровня ветвления в речная система.

Есть разные подходы[1] к топологический заказ реки или участки рек в зависимости от их удаленности от истока («сверху вниз»[2]) или из слияние (точка слияния двух рек) или устье реки ("вверх дном"[3]) и их иерархическое положение в речной системе. В качестве терминологии, как правило, используются слова «ручей» и «ветвь», а не «река».

Классический порядок потоковой передачи

Классический порядок потоковой передачи

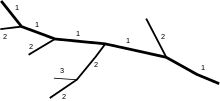
В классический порядок потоков, также называемый Взломать порядок потоков или Порядок ручья Гравелиуса, представляет собой иерархию «снизу вверх», которая присваивает номер «1» реке, устье которой находится в море ( главный стебель). это притоки дается номер один больше, чем у реки или ручья, в который они впадают. Так, например, всем непосредственным притокам главного ствола присвоен номер «2». Притоки, впадающие в «2», получают номер «3» и так далее.[4]

Такой порядок водотока указывает на место реки в сети. Подходит для общего картографический целей, но может создавать проблемы, потому что при каждом слиянии необходимо принимать решение о том, какая из двух ветвей является продолжением основного русла, и имеет ли главный канал свой источник в месте слияния двух других меньших потоков. Поток первого порядка - это тот, который при каждом слиянии имеет наибольший объемный поток, обычно отражающий давние названия рек. С этой системой распределения потоков связаны поиски географов 19-го века по поиску «истинного» источника реки. В ходе этой работы обсуждались и другие критерии, позволяющие определить основной поток. Помимо измерения длины рек (расстояния от самого дальнего источника до устья) и размера различных водосборы, географы искали ручей, который хотя бы отклонился от фактического слияния, а также принял во внимание последовательные названия рек и их притоков, таких как Рейн и Ааре или Эльба и Влтава.

Смотрите также: Закон взлома

Порядок потока Strahler

Порядок потока Strahler
Основная статья: Порядок потока Strahler

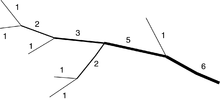
По системе «сверху вниз», разработанной Strahler, реки первого порядка - крайние притоки. Если два потока одного порядка объединяются, результирующему потоку присваивается номер на единицу больше. Если две реки с разными порядками потоков сливаются, результирующему потоку дается большее из двух чисел.[5][6]

Приказ Стралера призван отразить морфология из водосбор и составляет основу важных гидрографический показатели его структуры, такие как коэффициент бифуркации, плотность дренажа и частота. Его основой является водораздел линия водосбора. Однако это зависит от масштаба. Чем больше масштаб карты, тем больше порядков потока может быть обнаружено. Общая нижняя граница для определения «ручья» может быть установлена ​​путем определения его ширины в устье или, со ссылкой на карту, путем ограничения его протяженности. Сама система также применима для других небольших сооружений за пределами гидрологии.

Порядок ручья Шрива

Порядок ручья Шрива

В системе Шрива самым удаленным притокам также присвоен номер «1». В отличие от метода Strahler, при слиянии два числа складываются.[7]

Порядок потока Шрива предпочтителен в гидродинамика: он суммирует количество источников в каждом водосборе выше расходомер или отток, и примерно соответствует увольнять объемы и уровни загрязнения. Как и метод Strahler, он зависит от точности включенных источников, но в меньшей степени зависит от масштаба карты. Его можно сделать относительно независимым от масштаба, используя подходящую нормализацию, и тогда он будет в значительной степени независимым от точного знания верхнего и нижнего слоев области.[7]

Порядки хортонов и топологических потоков

Другие системы включают порядок потоков Хортона, раннюю систему сверху вниз, разработанную Роберт Э. Хортон,[8] и топологическая система порядка потоков, которая является системой «снизу вверх», и где порядковый номер потока увеличивается на единицу при каждом слиянии.[4]

Сравнение классического порядка потоков с методами Хортона и Стрелера

Классическим или топологическим системам упорядочивания присваивается безразмерный числовой порядок «единица», начиная с устья ручья, которое является его самой низкой точкой возвышения. Затем порядок векторов увеличивается по мере того, как он прослеживается вверх по течению и сходится с другими меньшими потоками, что приводит к корреляции чисел более высокого порядка с более высокогорными истоками.

Хортон предложил установить этот порядок в обратном порядке. В отчете об исследовании 1947 года Хортона был установлен метод упорядочения потоков, основанный на векторной геометрии. В 1952 г. Артур Стралер предложил модификацию метода Хортона. Оба метода - Хортона и Стралера - установили назначение самого низкого порядка, номер 1, начиная с верховья реки, которое является самой высокой точкой возвышения. Классическое присвоение порядковых номеров коррелирует с высотой и возвышением и трассировкой вверх по течению, но методы упорядочивания потоков Хортона и Стрелера коррелируют с гравитационным потоком и трассировкой вниз по течению.

Методы упорядочения потоков как Хортона, так и Стрелера основаны на принципах векторной точечной геометрии. Правила Хортона и Стрелера составляют основу алгоритмов программирования, которые интерпретируют данные карты как запрошенные Географические информационные системы.

Применение

Классическое использование порядка потоков - это общая гидрологическая картография. Системы порядка водотоков также важны для систематического картирования речной системы, позволяя четко маркировать и упорядочивать водотоки.

Методы Штралера и Шрива особенно ценны для моделирование и морфометрический анализ речных систем, потому что они определяют каждый участок реки. Это позволяет разделить сеть на каждом датчике или выходе на режимы вверх и вниз по потоку и классифицировать эти точки. Эти системы также используются в качестве основы для моделирования водного баланса с использованием моделей накопления или временных моделей, моделей выпадения и оттока и т.п.

в На базе ГИС В науках о Земле эти две модели используются, потому что они показывают графическую протяженность речного объекта.

Исследовательская деятельность после отчета Штралера 1952 года была сосредоточена на решении некоторых проблем при преобразовании двумерных карт в трехмерные векторные модели. Одна из проблем заключалась в преобразовании растровых пиксельных изображений потоков в векторный формат. Другая проблема заключалась в том, что настройки масштабирования карты при использовании ГИС может изменить классификацию потока на коэффициент или на один или два порядка. В зависимости от масштаба карты ГИС некоторые мелкие детали древовидной структуры речной системы могут быть потеряны.

Исследования частного сектора, университетов и федеральных правительственных агентств, таких как EPA и USGS объединили ресурсы и сосредоточили внимание на изучении этих и других проблем. Основная цель состоит в том, чтобы стандартизировать программное обеспечение и правила программирования, чтобы данные ГИС были стабильно надежными при любом масштабе карты. С этой целью EPA и USGS возглавили усилия по стандартизации, которые привели к созданию Национальная карта. Оба федеральных агентства, а также ведущие частные компании-производители программного обеспечения приняли принципы вектора порядка потоков Хортона и Стрелера в качестве основы для правил логики кодирования, встроенных в стандартизированное программное обеспечение National Map.

Смотрите также

Рекомендации

  1. ^ Кошицки, 2.3, стр. 12 и далее.
  2. ^ Вейшар, стр. 30.
  3. ^ Вейшар, стр. 35.
  4. ^ а б Описание на svn.osgeo.org, получено 16 апреля 2017 г.
  5. ^ Strahler (1957), 913-920.
  6. ^ Strahler (1964), 4-39, 4-76.
  7. ^ а б Шрив (1966), 17–37.
  8. ^ Хортон (1945), 275–370.

Источники

  • Дрвал, Дж. Wykształcenie i organacja sieci hydrograficznej jako podstawa oceny Struktury odpływu na terenach młodoglacjalnych, Rozprawy i monografie, Гданьск, 1982, 130 с. (На польском языке)
  • Хак, Дж. Исследования продольных профилей течения в Вирджинии и Мэриленде, U.S. Geological Survey Professional Paper, 1957, 294-B.
  • Хортон Р. Э., Эрозионное развитие водотоков и их водосборных бассейнов: гидрофизический подход к количественной морфологии, Бюллетень Геологического общества Америки 56 (3): 275-370, 1945.
  • Кошицки, Томас. GIS-basierte, automatische Erfassung natürlicher Fließgewässerhierarchien und ihre Abbildung в Datenbanken, beispielhaft dargestellt am Einzugsgebiet der Salza. Диссертация, Университет Мартина Лютера в Галле-Виттенберге, Галле (Заале), 2004 г., URN (NBN) урна: nbn: de: gbv: 3-000007179 (Интернет-ссылка, архивный сервер DNB)
  • Шайдеггер А. Э. (1966), Статистическое описание речных сетей. Водный ресурс. Res., 2 (4): 785-790.
  • Шрив Р. (1966), Статистический закон чисел потоков, J. Geol., 74, 17–37.
  • Стралер, А. Динамические основы геоморфологии. В: Бюллетень Геологического общества Америки 63/1952, стр. 923–938.
  • Стралер, А. Количественный анализ геоморфологии водоразделов. Труды Американского геофизического союза. 1957; 38 (6), стр. 913-920.
  • Стралер, А. «Количественная геоморфология водосборных бассейнов и русловых сетей». Чоу В.Т., редактор. Справочник по прикладной гидрологии. Нью-Йорк: Макгроу-Хилл; 1964; С. 4-39, 4-76.
  • Шрив, Р. Статистический закон чисел потока. В: Журнал геологии 74/1966.
  • Вейшар, Ли Л. Развитие гидрогеоморфологии болот и болотной растительности с участком восстановления заболоченных земель соляной фермы. Проверено 16 апр 2017.
  • Волденберг, М. Дж. (1967), География и свойства поверхностей, Гарвардские документы по теоретической географии, 1: 95-189.
  • Rivertool - Расширение для ArcView, документация по использованию, Управление прикладной гидрологии (Интернет-ссылка, gis-tools.de)

внешняя ссылка

  • Международный глоссарий гидрологии (файл в формате pdf; 1,24 МБ)
  • «Gewässernetz: номера для заказа водотоков для цифровой водопроводной сети, серия 1:25 000, Швейцария». Hydrologische Grundlagen und Daten - Informationssysteme und Methoden - Gewässernetz - Flussordnungszahlen (на немецком). Bundesamt für Umwelt BAFU. 4 апреля 2007 г.. Получено 8 марта 2008.