WikiDer > 85 способов завязать галстук
 | |
| Автор | Томас Финк и Юн Мао |
|---|---|
| Издатель | Четвертое сословие |
Дата публикации | 4 ноября 1999 г. |
| ISBN | 1-84115-249-8 |
| OCLC | 59397523 |
85 способов завязать галстук это книга Томас Финк и Юн Мао об истории завязанных шейный платок, современный галстук, и как связать оба. Он основан на двух математических работах, опубликованных авторами в Природа[1] и Physica A пока они были научные сотрудники в Кембриджском университете Кавендишская лаборатория.[2] Авторы доказывают, что, если предположить, что и галстук, и носитель имеют типичный размер, существует ровно 85 способов завязать галстук с использованием обычного метода обертывания широкого конца галстука вокруг узкого конца. Они описывают каждый и выделяют те, которые они считают исторически значимыми или эстетически привлекательными.
Это было опубликовано Четвертое сословие 4 ноября 1999 г., а затем опубликован на девяти других языках.
Математика
Открытие всех возможных способов завязать галстук зависит от математической формулировки процесса завязывания галстука. В своих статьях (которые носят технический характер) и книге (предназначенной для непрофессиональной аудитории, не считая приложения) авторы показывают, что завязывание галстуков эквивалентно стойкому случайные прогулки на треугольнике решетка, с некоторыми ограничениями на начало и конец прогулки. Таким образом, перечисляя узлы связи п ходов эквивалентно перечислению прогулок п шаги. Навязывание условий симметрия а баланс сокращает 85 узлов до 13 эстетических.
Представление узла
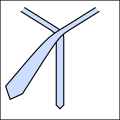
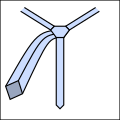
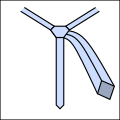
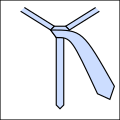
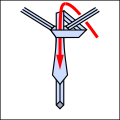
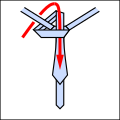
Основная идея состоит в том, что узлы можно описать как последовательность из пяти различных возможных ходов, хотя не все ходы могут следовать друг за другом. Их кратко можно описать следующим образом. На всех диаграммах такой галстук, если бы вы его надели и посмотрели в зеркало.
- L: оставили; C: центр; р: верно; они должны менять каждое движение.
- я: в диаграмму; о: вне диаграммы; они должны чередоваться.
- Т: через только что сделанную петлю.
С помощью этого сокращения можно компактно выразить традиционные и новые узлы, как показано ниже. Обратите внимание, что любой узел, начинающийся с о движение нужно начинать с завязки вокруг шеи наизнанку.
- Примеры завязывания узлов.
Узлы
Критерий отбора
Из 85 узлов, возможных для обычного галстука, Финк и Мао выбрали тринадцать как «эстетические узлы», пригодные для использования. Они сделали свой выбор по трем критериям: форма, симметрия и баланс.
Форма
Согласно классификации Финка и Мао, каждый из 85 узловых узлов принадлежит к определенному «классу», который определяется его общим количеством ходов и количеством центральных ходов. Например, четверка в руке - это четырехходовый узел с одним центром, а полу-Виндзор - это двухходовый узел с шестью ходами. Узлы с меньшим количеством центровочных ходов, менее одной трети от общего числа, кажутся более узкими и более вытянутыми, в то время как узлы с большим количеством центровочных ходов кажутся шире и более приземистыми. Из-за треугольной природы узловых узлов количество центровочных ходов обязательно должно быть меньше половины общего количества ходов.
Всего существует 16 классов, от трех движений с одним центром до девяти движений с четырьмя центрами, но только классы, в которых отношение центровочных движений к общему количеству движений составляет 1: 6 или больше, содержат эстетический узел, исключая три класса ( десять узлов) для оставшихся 13 классов со скоростью 75 узлов. (В Природа В документе нижняя граница была помещена в более ограничительное значение 1: 4, исключая классы узлов, содержащие Кельвина, Виктории и Грантчестера; это, вероятно, было специально пересмотрено, чтобы включить Викторию / принца Альберта, который имеет довольно обширную историческую документацию.) Затем был выбран наиболее представительный узел в каждом оставшемся классе на основе симметрии и баланса.
Симметрия
Симметрия в случае узловых узлов может относиться к двум возможным качествам: визуальный симметрия (степень, в которой узел выглядит одинаково с левой и правой стороны), и математический симметрия (количество ходов L и R максимально близко к равному). Финк и Мао относятся к последнему, хотя некоторые узлы, которые слегка асимметричны (такие как Ники и Виндзор), кажутся симметричными для глаза. Только узлы с равным количеством ходов L и R могут быть математически симметричными, в то время как остальные эстетические узлы обязательно будут иметь на один больший ход L или R.
Баланс
Финк и Мао описывают баланс как «степень, в которой движения хорошо смешаны», ссылаясь на более плотный узел, который с трудом развязывается, как на его главное достоинство. Он рассчитывается по определенной формуле, но неспециалист может лучше всего понять его как степень, в которой движения L, R и C равномерно распределены по всей последовательности завязывания узлов, и степень, в которой паттерн LR или RL продолжается без прерывания после нетерминальные центрирующие движения (что требует изменения направления намотки с против часовой стрелки на по часовой стрелке или наоборот). Эти качества проявляются в каждом из эстетических узлов.
Ряд узлов имеют практически идентичные варианты, которые отличаются перестановкой пар L и R. Например, вариант полу-Виндзора, Ли Ро Ци Ло Ри Ко Т (узел 7), представляет собой узел Ли Ро Си Ро Ли Ко Т (узел 8), иногда называемый совместным полу-Виндзором. Ссылки на Half-Windsor в литературе иногда относятся к одному, иногда к другому. Для целей книги, когда узел имеет хотя бы один вариант (т. Е. Когда два или более узлов с наибольшей степенью симметрии для своего класса разделяют одну и ту же базовую структуру, кроме одной или нескольких транспонированных пар LR), наиболее сбалансированной версии присваивается стандартное обозначение, в то время как другие маркируются как варианты, независимо от таких качеств, как саморазъем (отключается при вытаскивании узкого конца). Таким образом, более сбалансированный из двух «полу-виндзорских» узлов получает более низкую нумерацию и название «полу-Виндзор», хотя немного менее сбалансированный вариант «полу-виндзорского» одинаково известен как «полу-виндзорский». Виндзор »в литературе по мужскому стилю, и имеет то преимущество, что самораспускается, а наиболее распространенный способ завязывания Виндзорского узла Финк и Мао называют« co-Windsor 3 ». Однако это не предназначено для обозначения эстетического предпочтения одного варианта над другим; как отмечают авторы в своих журнальных статьях: «Мы не пытаемся проводить различие между этими узлами и их аналогами; это оставляем на усмотрение читателя».
Три эстетических узла (Сент-Эндрю, Кавендиш и Грантчестер) имеют те же значения симметрии и баланса, что и по крайней мере еще один узел в своем классе; в этом случае они, по-видимому, были выбраны на основании того, насколько равномерно они распределяют несбалансированные части по узлу. Это легко увидеть, если рассматривать эти сучки как комбинации двух меньших сучков, поскольку значения баланса каждого компонента складываются в значение баланса последнего узла. В неуравновешенных узлах, где значение баланса нечетное, оно разбивается, так что более неуравновешенная часть из двух оказывается ближе к началу узла. Вероятно, это сделано для того, чтобы внешняя часть узла сохраняла форму и оставалась тугой.
13 эстетических узлов
Тринадцать эстетических узлов, описанных в книге в порядке их размера, следующие. Конечные последовательности (последние три хода, которые заканчиваются связыванием узла) выделены жирным шрифтом. Иногда узелки обозначают только их номером (например, FM2 для четверки, с FM означает Финк-Мао). Узел самораспускается, если при протягивании тонкого конца через узел не остается узла; поскольку все узлы начинаются слева, узел самораспускается, если конечная последовательность Ро Ли Ко; это нет самоотпускание, если конечная последовательность Lo Ri Co. Симметрия и самораспускание дополняют друг друга для узлов с наибольшей степенью сбалансированности для своего класса.
| Число | Последовательность | Имя | Самовыпускание | Симметричный[3] |
|---|---|---|---|---|
| 1. | Ло Ри Ко Т | Узелок | Нет | да |
| 2. | Ли Ро Ли Ко Т | Четыре в руке | да | Нет |
| 3. | Ло Ри Ло Ри Ко Т | Кельвин | Нет | да |
| 4. | Lo Ci Ро Ли Ко Т | Ники (самовыпускается Пратт) | да | Нет |
| 6. | Ли Ро Ли Ро Ли Ко Т | Виктория | да | Нет |
| 7. | Ли Ро Ки Ло Ри Ко Т | Half-Windsor | Нет | да |
| 12. | Ло Ри Ло Ки Ро Ли Ко Т | Святой Андрей | да | Нет |
| 18. | Ло Чи Ро Ки Ло Ри Ко Т | Plattsburgh | Нет | да |
| 23. | Ли Ро Ли Ко Ри Ло Ри Ко Т | Кавендиш | Нет | да |
| 31. | Ли Ко Ри Ло Ки Ро Ли Ко Т | Виндзор | да | Нет |
| 44. | Ло Ри Ло Ри Ко Ли Ро Ли Ко Т | Grantchester | да | Нет |
| 54. | Ло Ри Ко Ли Ро Ки Ло Ри Ко Т | Ганновер | Нет | да |
| 78. | Ло Чи Ро Чи Ло Ки Ро Ли Ко Т | Balthus | да | Нет |
Три распространенных варианта узла следующие. Они включены из-за их общности (Пратт, вариант Полувиндзора) или для того, чтобы самораспускаться, когда их более «эстетичные» аналоги нет (вариант Полувиндзор, вариант Ганновера). Варианты Half-Windsor и Hanover имеют то преимущество, что они симметричны и самораспускаются, но они менее сбалансированы, чем их аналоги выше:
| Число | Последовательность | Имя | Самовыпускание | Симметричный[3] |
|---|---|---|---|---|
| 5. | Lo Ci Ло Ри Ко Т | Пратт | Нет | Нет |
| 8. | Ли Ро Ки Ро Ли Ко Т | Вариант Half-Windsor | да | да |
| 55. | Ло Ри Ко Ри Ло Ки Ро Ли Ко Т | Ганноверский вариант | да | да |
Отзывы
Книга была рецензирована в Природа,[4] Дейли Телеграф, Хранитель, GQ, Мир физики, и другие.
Рекомендации
- ^ Финк, Томас М.; Юн Мао (1999). «Создание узлов для галстука путем случайных прогулок» (PDF). Природа. 398 (6722): 31–32. Дои:10.1038/17938.
- ^ Финк, Томас М.; Юн Мао (2000). «Узлы завязки, случайные блуждания и топология» (PDF). Physica A. 276 (1–2): 109–121. Дои:10.1016 / S0378-4371 (99) 00226-5.
- ^ а б Энциклопедия галстуков на домашней странице Томаса Финка
- ^ Бак, Грегори (2000). «Почему не завязать узел?». Природа. 403 (6768): 362. Дои:10.1038/35000270.
внешняя ссылка
| В Викиучебнике есть книга на следующие темы: Как завязать галстук |
- Узлы галстуков в Керли
- Учебник Джеффа Бэнкса по Как завязать галстук