WikiDer > Трамвай Архимеда

Trammel of Archimedes

Анимированная модель "Трамвай Архимеда".

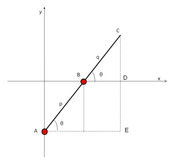
А трамвай архимеда это механизм который создает форму эллипс.^[1] Он состоит из двух челноков, которые ограничены ("протоптаны") в перпендикулярных каналах или рельсах, и стержня, который прикреплен к челнокам с помощью шарниров в фиксированных положениях вдоль стержня.

По мере того как челноки движутся вперед и назад, каждый по своему каналу, все точки на стержне движутся по эллиптическим траекториям. Движение стержня называется эллиптическим движением. Полуоси а и б эллипсов имеют длину, равную расстояниям от точки на стержне до каждого из двух стержней.

Прямые линии, описываемые поворотными точками, являются частными случаями эллипса, где длина одной оси в два раза больше расстояния между поворотными точками, а длина другой равна нулю. Все точки на окружности с диаметром, определяемым двумя шарнирами, совершают возвратно-поступательное движение по таким прямым линиям. Этот круг соответствует меньшему кругу в Пара туси.

Точка на полпути между опорами вращается по кругу вокруг точки пересечения каналов. Этот круг также является частным случаем эллипса. Здесь оси одинаковой длины. Диаметр круга равен расстоянию между стержнями. Направление движения по орбите противоположно направлению вращения трамвая. Таким образом, если кривошип, расположенный в точке пересечения каналов, используется для включения трамбовки в средней точке, чтобы привести ее в движение, вращение шейки кривошипа и трамбовки будет равным и противоположным, что на практике приводит к дополнительному трению и ускорению. носить. Это усугубляется высокими усилиями из-за короткого хода кривошипа, составляющего лишь 1/4 хода шарниров.

An эллипсограф представляет собой трамбовку Архимеда, предназначенную для рисования, вырезания или обработки эллипсов, например в дерево или другие листовые материалы. В эллипсографе есть соответствующий инструмент (карандаш, нож, маршрутизатори т. д.), прикрепленные к стержню. Обычно расстояния а и б регулируются, так что размер и форму эллипса можно варьировать.

История таких эллипсографов неизвестна, но считается, что они восходят к Прокл и, возможно, даже ко времени Архимед.^[2]

Деревянные версии трамвая Архимеда производились также как игрушки или же новинки, и продается под названием Кентукки бездельники, ничего болгарки, ничего не делать машины, коптильни, или же болгарки. В этих игрушках чертежный инструмент заменен на заводить ручка, а положение выдвижных челноков обычно фиксируется.

Математика

Концепция

Траммель Архимеда как эллипсограф
Диаграмма
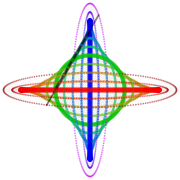
Локусы некоторых точек вдоль и за пределами трамвая Архимеда, зеленый кружок - это локусы его средней точки - в файле SVG, наведите указатель на диаграмму, чтобы переместить трамвай
Трамвай Архимеда с тремя ползунками

Позволять C быть внешним концом стержня, и А, B быть стержнями ползунков. Позволять п и q быть расстояниями от А к B и B к C, соответственно. Предположим, что ползунки А и B двигаться по у и Икс координировать оси соответственно. Когда стержень делает угол θ с Икс-ось, координаты точки C даны

{ Displaystyle х = (п + д) соз тета ,}

{ Displaystyle у = д грех тета ,}

Они представлены в виде стандартных параметрических уравнений для эллипса в каноническом положении. Дальнейшее уравнение

{ displaystyle { frac {x ^ {2}} {(p + q) ^ {2}}} + { frac {y ^ {2}} {q ^ {2}}} = 1}

также немедленно.

Трамвай Архимеда является примером четырехзвенная навеска с двумя ползунками и двумя шарнирами, и является частным случаем более общего наклонного трамплина. Оси, ограничивающие шарниры, не должны быть перпендикулярными, а точки А, B и C может образовывать треугольник. Результирующий локус C по-прежнему эллипс.^[2]

Примеры исторических устройств