WikiDer > Линейный матричный метод

В метод матрицы линий передачи (TLM) представляет собой метод дискретизации пространства и времени для вычисления электромагнитные поля. Он основан на аналогия между электромагнитным полем и сеткой линии передачи. Метод TLM позволяет рассчитывать сложные трехмерные электромагнитные структуры и зарекомендовал себя как один из самых мощных методов временной области наряду с конечной разностью временной области (FDTD) метод.

Основной принцип

Пример 2D TLM: падающий импульс напряжения в двух последовательных событиях рассеяния.

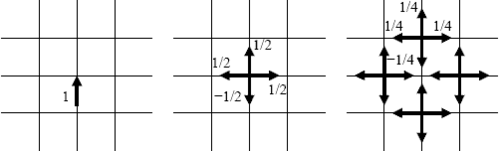
Метод TLM основан на Модель распространения волн Гюйгенса рассеяние и аналогия между распространением поля и линиями передачи. Следовательно, он рассматривает вычислительную область как сеть линий передачи, соединенных между собой в узлах. На рисунке справа рассматривается простой пример 2D-сетки TLM с импульсом напряжения амплитудой 1 В, падающим на центральный узел. Этот импульс будет частично отражен и передан в соответствии с теорией линии передачи. Если предположить, что каждая линия имеет характеристический импеданс ${ displaystyle Z}$, то падающий импульс фактически видит три линии передачи, параллельные с общим импедансом ${ displaystyle Z / 3}$. Коэффициент отражения и коэффициент передачи определяются выражением

${ Displaystyle R = { frac {Z / 3-Z} {Z / 3 + Z}} = - 0,5}$

${ Displaystyle Т = { гидроразрыва {2 (Z / 3)} {Z / 3 + Z}} = 0,5}$

Энергия, вводимая в узел падающим импульсом, и полная энергия рассеянных импульсов соответственно равны

${ Displaystyle E_ {I} = vi , Delta t = 1 left (1 / Z right) Delta t = Delta t / Z}$

${ displaystyle E_ {S} = left [0,5 ^ {2} + 0,5 ^ {2} + 0,5 ^ {2} + (- 0,5) ^ {2} right] ( Delta t / Z) = Delta т / з}$

Следовательно закон сохранения энергии выполняется по модели.

Следующее событие рассеяния возбуждает соседние узлы по принципу, описанному выше. Видно, что каждый узел превращается во вторичный источник сферической волны. Эти волны объединяются, чтобы сформировать общую форму волны. Это соответствует принципу распространения света Гюйгенса.

Чтобы показать схему TLM, мы воспользуемся дискретизацией времени и пространства. Шаг по времени будет обозначен ${ displaystyle Delta t}$ и интервалы дискретизации пространства с ${ displaystyle Delta x}$, ${ displaystyle Delta y}$ и ${ displaystyle Delta z}$. Следовательно, абсолютное время и пространство будут ${ Displaystyle т = к , дельта т}$, ${ displaystyle x = l , Delta x}$, ${ Displaystyle у = м , Дельта у}$, ${ Displaystyle Z = N , Delta Z}$, куда ${ Displaystyle к = 0,1,2, ldots}$ это момент времени и ${ displaystyle m, n, l}$ - координаты ячейки. В случае ${ Displaystyle Delta x = Delta y = Delta z}$ Значение ${ displaystyle Delta l}$ будет использоваться, что является постоянная решетки. В этом случае имеет место следующее:

${ displaystyle Delta t = { frac { Delta l} {c_ {0}}},}$

куда ${ displaystyle c_ {0}}$ - это скорость света в свободном пространстве.

Узел 2D TLM

Матрица рассеяния узла 2D TLM

Узел TLM серии 2D

Если мы рассмотрим распределение электромагнитного поля, в котором единственными ненулевыми компонентами являются ${ displaystyle E_ {x}}$, ${ displaystyle E_ {y}}$ и ${ displaystyle H_ {z}}$ (т.е.распределение TE-моды), то уравнения Максвелла в Декартовы координаты сократить до

${ displaystyle { frac { partial {H_ {z}}} { partial {y}}} = varepsilon { frac { partial {E_ {x}}} { partial {t}}}}$

${ displaystyle - { frac { partial {H_ {z}}} { partial {x}}} = varepsilon { frac { partial {E_ {y}}} { partial {t}}}}$

${ displaystyle { frac { partial {E_ {y}}} { partial {x}}} - { frac { partial {E_ {x}}} { partial {y}}} = - mu { frac { partial {H_ {z}}} { partial {t}}}}$

Мы можем объединить эти уравнения, чтобы получить

${ displaystyle { frac { partial ^ {2} H_ {z}} { partial {x} ^ {2}}} + { frac { partial ^ {2} {H_ {z}}} { partial {y} ^ {2}}} = mu varepsilon { frac { partial ^ {2} {H_ {z}}} { partial {t} ^ {2}}}}$

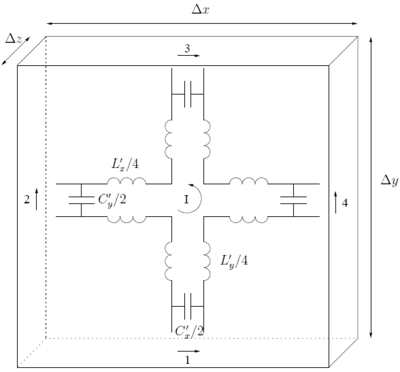
На рисунке справа представлена ​​конструкция, называемая узел серии. Он описывает блок пространственных измерений ${ displaystyle Delta x}$, ${ displaystyle Delta y}$ и ${ displaystyle Delta z}$ который состоит из четырех портов. ${ displaystyle L '}$ и ${ displaystyle C '}$ - распределенная индуктивность и емкость линий передачи. Можно показать, что последовательный узел эквивалентен TE-волне, а точнее сетке тока. я, то Икс-направленные напряжения (порты 1 и 3) и у-направленные напряжения (порты 2 и 4) могут быть связаны с полевыми компонентами ${ displaystyle H_ {z}}$, ${ displaystyle E_ {x}}$ и ${ displaystyle E_ {y}}$. Если учитывать напряжения на портах, ${ Displaystyle L_ {x} = L_ {y}}$, и полярность из рисунка выше, то верно следующее

${ displaystyle -V_ {1} + V_ {2} + V_ {3} -V_ {4} = 2L ', Delta l { frac { partial {I}} { partial {t}}}}$

куда ${ Displaystyle Delta x = Delta y = Delta l}$.

${ displaystyle left (V_ {3} -V_ {1} right) - left (V_ {4} -V_ {2} right) = 2L ', Delta l { frac { partial I} { partial t}}}$

${ displaystyle left [E_ {x} (y + Delta y) -E_ {x} (y) right] , Delta x- [E_ {y} (x + Delta x) -E_ {y} ( x)] Delta y = 2L ', Delta l { frac { partial {I}} { partial {t}}}}$

и разделив обе стороны на ${ displaystyle Delta x Delta y}$

${ displaystyle { frac {E_ {x} (y + Delta y) -E_ {x} (y)} { Delta y}} - { frac {E_ {y} (x + Delta x) -E_ { y} (x)} { Delta x}} = 2L ', Delta l { frac { partial {I}} { partial {t}}} { frac {1} { Delta x , Delta y}}}$

С ${ Displaystyle Delta x = Delta y = Delta z = Delta l}$ и заменяя ${ Displaystyle I = H_ {z} , Delta z}$ дает

${ displaystyle { frac { Delta E_ {x}} { Delta y}} - { frac { Delta E_ {y}} { Delta x}} = 2L '{ frac { partial H_ {z }} { partial t}}}$

Это сводится к уравнениям Максвелла, когда ${ displaystyle Delta l rightarrow 0}$.

Аналогично, используя условия на конденсаторах на портах 1 и 4, можно показать, что соответствующие два других уравнения Максвелла следующие:

${ displaystyle { frac { partial {H_ {z}}} { partial {y}}} = C '{ frac { partial {E_ {x}}} { partial {t}}}}$

${ displaystyle - { frac { partial {H_ {z}}} { partial {x}}} = C '{ frac { partial {E_ {y}}} { partial {t}}}}$

Имея эти результаты, можно вычислить матрицу рассеяния шунтирующего узла. Импульс напряжения, падающий на порт 1 с шагом k обозначается как ${ displaystyle _ {k} V_ {1} ^ {i}}$. Заменив четыре отрезка линии с рисунка выше на их Эквивалент Тевенина можно показать, что выполняется следующее уравнение для отраженного импульса напряжения:

${ displaystyle _ {k} V_ {1} ^ {r} = 0,5 left (_ {k} V_ {1} ^ {i} + _ {k} V_ {2} ^ {i} + _ {k} V_ {3} ^ {i} -_ {k} V_ {4} ^ {i} right)}$

Если все падающие волны, а также все отраженные волны собраны в один вектор, то это уравнение можно записать для всех портов в матричной форме:

${ Displaystyle _ {к} mathbf {V} ^ {r} = mathbf {S} _ {k} mathbf {V} ^ {i}}$

куда ${ Displaystyle _ {к} mathbf {V} ^ {я}}$ и ${ Displaystyle _ {к} mathbf {V} ^ {r}}$ - векторы амплитуд падающего и отраженного импульса.

Для узла серии матрица рассеяния S имеет следующий вид

${ displaystyle mathbf {S} = { frac {1} {2}} left [{ begin {array} {cccc} 1 & 1 & 1 & -1 1 & 1 & -1 & 1 1 & -1 & 1 & 1 - 1 & 1 & 1 & 1 end {array}} right]}$

Связь между узлами TLM

Узел TLM серии 2D

Чтобы описать связь между соседними узлами сеткой последовательных узлов, посмотрите на рисунок справа. Поскольку падающий импульс в временном шаге к + 1 на узле - это рассеянный импульс от соседнего узла в интервале времени k, выводятся следующие уравнения связи:

${ displaystyle _ {k + 1} V_ {1} ^ {i} (x, y) = _ {k + 1} V_ {3} ^ {r} (x, y-1)}$

${ displaystyle _ {k + 1} V_ {2} ^ {i} (x, y) = _ {k + 1} V_ {4} ^ {r} (x-1, y)}$

${ displaystyle _ {k + 1} V_ {3} ^ {i} (x, y) = _ {k + 1} V_ {1} ^ {r} (x, y + 1)}$

${ displaystyle _ {k + 1} V_ {4} ^ {i} (x, y) = _ {k + 1} V_ {2} ^ {r} (x + 1, y)}$

Изменяя матрицу рассеяния ${ displaystyle { textbf {S}}}$ можно моделировать неоднородные материалы и материалы с потерями. Регулируя уравнения связи, можно моделировать различные границы.

Шунтирующий узел TLM

Помимо узла серии, описанного выше, есть еще шунтирующий узел TLM, который представляет собой распределение поля TM-моды. Единственными ненулевыми составляющими такой волны являются ${ displaystyle H_ {x}}$, ${ displaystyle H_ {y}}$, и ${ displaystyle E_ {z}}$. Принимая во внимание те же соображения, что и для последовательного узла, можно получить матрицу рассеяния для шунтирующего узла.

3D модели TLM

Трехмерный симметричный конденсированный узел

Для большинства задач в электромагнетизме требуется трехмерная сетка. Поскольку теперь у нас есть структуры, которые описывают распределения TE и TM-поля, интуитивно кажется возможным определить комбинацию шунтирующих и последовательных узлов, обеспечивающих полное описание электромагнитного поля. Такие попытки предпринимались, но из-за сложности полученных структур они оказались не очень полезными. Использование аналогии, представленной выше, приводит к вычислению различных компонент поля в физически разделенных точках. Это вызывает трудности с предоставлением простых и эффективных определений границ. Решение этих проблем было предложено Джонс в 1987 году, когда он предложил структуру, известную как симметричный конденсированный узел (SCN), представленный на рисунке справа. Он состоит из 12 портов, потому что две поляризации поля должны быть назначены каждой из 6 сторон ячейки.

Топологию SCN нельзя анализировать с помощью эквивалентных схем Тевенина. Необходимо использовать более общие принципы сохранения энергии и заряда.

Электрическое и магнитное поля по сторонам номера узла SCN (l, m, n) в момент времени k можно представить в виде 12-мерных векторов

${ displaystyle _ {k} mathbf {E} _ {l, m, n} = _ {k} left [E_ {1}, E_ {2}, ldots, E_ {11}, E_ {12} right] _ {l, m, n} ^ {T}}$

${ displaystyle _ {k} mathbf {H} _ {l, m, n} = _ {k} left [H_ {1}, H_ {2}, ldots, H_ {11}, H_ {12} right] _ {l, m, n} ^ {T}}$

Их можно связать с векторами падающей и рассеянной амплитуд через

${ displaystyle _ {k} mathbf {a} _ {l, m, n} = { frac {1} {2 { sqrt {Z_ {F}}}}} {_ {k} mathbf {E }} _ {l, m, n} + { frac { sqrt {Z_ {F}}} {2}} {_ {k} mathbf {H}} _ {l, m, n}}$

${ displaystyle _ {k} mathbf {b} _ {l, m, n} = { frac {1} {2 { sqrt {Z_ {F}}}}} {_ {k} mathbf {E }} _ {l, m, n} - { frac { sqrt {Z_ {F}}} {2}} {_ {k} mathbf {H}} _ {l, m, n}}$

куда ${ Displaystyle Z_ {F} = { sqrt { frac { mu} { varepsilon}}}}$ - полное сопротивление поля, ${ displaystyle _ {k} mathbf {a} _ {l, m, n}}$ - вектор амплитуд падающих волн на узел, а ${ displaystyle _ {k} mathbf {b} _ {l, m, n}}$ - вектор рассеянных амплитуд. Связь между падающей и рассеянной волнами дается матричным уравнением

${ displaystyle _ {k} mathbf {b} _ {l, m, n} = mathbf {S} _ {k} mathbf {a} _ {l, m, n}}$

Матрица рассеяния S можно рассчитать. Для симметричного конденсированного узла с портами, обозначенными как на рисунке, получается следующий результат

${ displaystyle mathbf {S} = left [{ begin {array} {ccc} 0 & mathbf {S} _ {0} & mathbf {S} _ {0} ^ {T} mathbf { S} _ {0} ^ {T} & 0 & mathbf {S} _ {0} mathbf {S} _ {0} & mathbf {S} _ {0} ^ {T} & 0 end {array }}верно]}$

где использовалась следующая матрица

${ displaystyle mathbf {S} _ {0} = { frac {1} {2}} left [{ begin {array} {cccc} 0 & 0 & 1 & -1 0 & 0 & -1 & 1 1 & 1 & 0 & 0 1 & 1 & 0 & 0 конец {массив}} right]}$

Соединение между различными SCN осуществляется таким же образом, как и для 2D-узлов.

Реализация 3D-TLM с открытым исходным кодом

В Джордж Грин Институт исследований электромагнетизма (GGIEMR) предоставил открытый исходный код эффективной реализации 3D-TLM, способной параллельное вычисление посредством MPI назван GGITLM и доступен в Интернете. ^[1]

Рекомендации

• К. Христопулос, Метод моделирования линии передачи: TLM, Piscataway, NY, IEEE Press, 1995. ISBN 978-0-19-856533-8
• Рассер П., Электромагнетизм, проектирование микроволновых цепей и антенн для техники связи, второе издание, Artec House, Бостон, 2006 г. ISBN 978-1-58053-907-4
• П. Б. Джонс и М. О'Брайен. «Использование метода моделирования линии передачи (t.l.m) для решения нелинейных сосредоточенных сетей», The Radio Electron and Engineer. 1980 г.
• Дж. Л. Херринг, Развитие метода моделирования линии передачи для исследований электромагнитной совместимости, Кандидатская диссертация, Ноттингемский университет, 1993.
• Мансур Ахмадиан, Матрица трансмиссионных линий (TLM), моделирование медицинского ультразвука Кандидатская диссертация, Эдинбургский университет 2001 г.