WikiDer > AC0
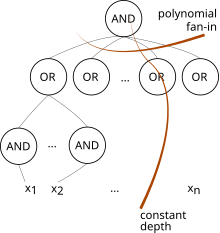
AC0 это класс сложности используется в сложность схемы. Это самый маленький класс в AC иерархии и состоит из всех семейств схем глубины O (1) и полиномиального размера с неограниченнымфанин И ворота и ИЛИ ворота. (Мы разрешаем НЕ ворота только на входах).[1] Таким образом, он содержит NC0, который имеет только ограниченные вентили И и ИЛИ.[1]
Примеры проблем
Сложение и вычитание целых чисел вычислимы в AC0,[2] но умножение - нет (по крайней мере, не в обычном двоичном или десятичном представлении целых чисел).
Поскольку это класс схемы, например П / поли, AC0 также содержит все унарный язык.
Описательная сложность
Из описательная сложность смотровая площадка, DLOGTIME-униформа AC0 равен описательному классу FO+ БИТ всего языки описывается в логике первого порядка с добавлением Предикат BIT, или альтернативно FO (+, ×), или Машина Тьюринга в логарифмическая иерархия.[3]
Разлуки
В 1984 году Ферст, Сакс и Sipser показал, что расчет паритет входа не может быть определено никаким AC0 схем, даже с неоднородностью.[4][1]Отсюда следует, что AC0 не равно NC1, потому что семейство схем в последнем классе может вычислять четность.[1] Более точные оценки следуют из лемма о переключении. Используя их, было показано, что существует разделение оракула между полиномиальная иерархия и PSPACE.
Рекомендации
- ^ а б c d Арора, Санджив; Варак, Вооз (2009). Вычислительная сложность. Современный подход. Издательство Кембриджского университета. стр.117–118, 287. ISBN 978-0-521-42426-4. Zbl 1193.68112.
- ^ Баррингтон, Дэвид Микс; Масиэль, Алексис (18 июля 2000 г.). «Лекция 2: Сложность некоторых проблем» (PDF). Летняя сессия IAS / PCMI 2000, Программа бакалавриата по математике глины: базовый курс вычислительной сложности.
- ^ Иммерман, Н. (1999). Описательная сложность. Springer. п.85.
- ^ Ферст, Меррик; Сакс, Джеймс Б.; Сипсер, Майкл (1984). «Четность, схемы и полиномиальная иерархия». Математическая теория систем. 17 (1): 13–27. Дои:10.1007 / BF01744431. МИСТЕР 0738749. Zbl 0534.94008.