WikiDer > Аддитивный синтез
Аддитивный синтез это синтез звука техника, которая создает тембр добавляя синус волны вместе.[1][2]
Тембр музыкальных инструментов можно рассматривать в свете Теория Фурье состоять из нескольких гармонический или негармоничный частичные или же обертоны. Каждая часть представляет собой синусоидальную волну разных частота и амплитуда который со временем набухает и распадается из-за модуляция из Конверт ADSR или же низкочастотный генератор.
Аддитивный синтез непосредственно генерирует звук, добавляя выходной сигнал нескольких генераторов синусоидальной волны. Альтернативные реализации могут использовать предварительно вычисленные волновые таблицы или наоборот Быстрое преобразование Фурье.
Объяснение
Звуки, которые слышны в повседневной жизни, не характеризуются ни одним частота. Вместо этого они состоят из суммы чистых синусоидальных частот, каждая из которых имеет разные значения. амплитуда. Когда люди слышат эти частоты одновременно, мы можем распознать звук. Это верно как для «немузыкальных» звуков (например, плеск воды, шелест листьев и т. Д.), Так и для «музыкальных звуков» (например, ноты фортепиано, птичьего твита и т. Д.). Этот набор параметров (частоты, их относительные амплитуды и то, как относительные амплитуды меняются с течением времени) заключен в тембр звука. Анализ Фурье это метод, который используется для определения этих точных параметров тембра из общего звукового сигнала; наоборот, результирующий набор частот и амплитуд называется Ряд Фурье исходного звукового сигнала.
В случае музыкальной ноты самая низкая частота ее тембра обозначается как звуковая основная частота. Для простоты мы часто говорим, что нота играет на этой основной частоте (например, "средний C составляет 261,6 Гц "),[3] хотя звук этой ноты состоит также из многих других частот. Набор остальных частот называется обертоны (или гармоники, если их частоты кратны основной частоте) звука.[4] Другими словами, только основная частота отвечает за высоту ноты, а обертоны определяют тембр звука. Обертоны фортепьяно, играющего среднюю до, будут сильно отличаться от обертонов скрипки, играющей ту же ноту; это то, что позволяет нам различать звуки двух инструментов. Между разными версиями одного и того же инструмента (например, пианино против рояль).
Аддитивный синтез направлен на использование этого свойства звука для создания тембра с нуля. Путем сложения чистых частот (синусоидальные волны) различных частот и амплитуд, мы можем точно определить тембр звука, который хотим создать.
Определения
Гармонический аддитивный синтез тесно связан с концепцией Ряд Фурье это способ выразить периодическая функция как сумма синусоидальный функции с частоты равняется целому числу, кратному обыкновенному основная частота. Эти синусоиды называются гармоники, обертоны, или вообще, частичные. В общем, ряд Фурье содержит бесконечное количество синусоидальных компонентов без верхнего предела частоты синусоидальных функций и включает ОКРУГ КОЛУМБИЯ компонент (один с частотой 0 Гц). Частоты за пределами слышимого человеком диапазона может быть опущен в аддитивном синтезе. В результате в аддитивном синтезе моделируется только конечное число синусоидальных членов с частотами, лежащими в пределах слышимого диапазона.
Форма волны или функция называется периодический если
для всех и на какой-то период .
В Ряд Фурье периодической функции математически выражается как:
куда
- это основная частота формы волны и равно обратной величине периода,
- это амплитуда из -я гармоника,
- это фазовый сдвиг из -я гармоника. atan2() - четырехквадрантный арктангенс функция
Будучи неслышным, ОКРУГ КОЛУМБИЯ компонент, , и все компоненты с частотами выше некоторого конечного предела, , опускаются в следующих выражениях аддитивного синтеза.
Гармоническая форма
Математически простейший гармонический аддитивный синтез можно выразить как:
- ,
(1)
куда это выход синтеза, , , и - соответственно амплитуда, частота и фазовый сдвиг -я гармоническая составляющая всего гармонические парциальные, и это основная частота формы волны и частота музыкальной ноты.
Зависящие от времени амплитуды
 | Пример гармонического аддитивного синтеза, в котором каждая гармоника имеет зависящую от времени амплитуду. Основная частота составляет 440 Гц. Проблемы с прослушиванием этого файла? Видеть Помощь СМИ |
В более общем смысле, амплитуда каждой гармоники может быть задана как функция времени, , в этом случае выход синтеза
- .
(2)
Каждый конверт должен медленно меняться относительно частотного интервала между соседними синусоидами. В пропускная способность из должно быть значительно меньше, чем .
Негармоническая форма
Аддитивный синтез может также производить негармоничный звуки (которые апериодический волны), в которых отдельные обертоны не обязательно должны иметь частоты, которые являются целыми кратными некоторой общей основной частоте.[5][6] Хотя многие традиционные музыкальные инструменты имеют гармонические составляющие (например, гобой), некоторые имеют негармонические частичные (например, колокола). Негармонический аддитивный синтез можно описать как
куда постоянная частота -я частичная.
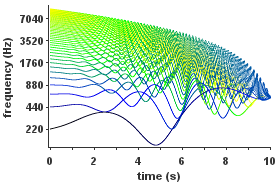 | Пример негармонического аддитивного синтеза, в котором амплитуда и частота каждой части зависят от времени. Проблемы с прослушиванием этого файла? Видеть Помощь СМИ |
Частоты, зависящие от времени
В общем случае мгновенная частота синусоиды - это производная (по времени) аргумента функции синуса или косинуса. Если эта частота представлена в герц, а не в угловая частота форме, то эта производная делится на . Это справедливо независимо от того, является ли парциальное значение гармоническим или негармоническим, и независимо от того, является ли его частота постоянной или изменяющейся во времени.
В самом общем виде частота каждой негармонической части является неотрицательной функцией времени, , уступая
(3)
Более широкие определения
Аддитивный синтез в более широком смысле может означать методы синтеза звука, которые суммируют простые элементы для создания более сложных тембров, даже если эти элементы не являются синусоидальными волнами.[7][8] Например, Ф. Ричард Мур назвал аддитивный синтез одной из «четырех основных категорий» звукового синтеза наряду с субтрактивный синтез, нелинейный синтез и физическое моделирование.[8] В этом широком смысле органы трубы, которые также имеют трубы, генерирующие несинусоидальные сигналы, могут рассматриваться как вариант формы аддитивных синтезаторов. Суммирование основные компоненты и Функции Уолша также были классифицированы как аддитивный синтез.[9]
Методы реализации
Современные реализации аддитивного синтеза в основном цифровые. (См. Раздел Уравнения с дискретным временем для основной теории дискретного времени)
Синтез банка осцилляторов
Аддитивный синтез может быть реализован с использованием банка синусоидальных генераторов, по одному на каждую частичку.[1]
Волновой синтез
В случае гармонических, квазипериодических музыкальных тонов волновой синтез может быть таким же общим, как нестационарный аддитивный синтез, но требует меньше вычислений во время синтеза.[10][11] В результате эффективная реализация нестационарного аддитивного синтеза гармонических тонов может быть достигнута с помощью волновой синтез.
Групповой аддитивный синтез
Групповой аддитивный синтез[12][13][14] - это метод группировки парциальных частиц в группы гармоник (имеющих разные основные частоты) и синтез каждой группы отдельно с помощью волновой синтез перед смешиванием результатов.
Обратный синтез БПФ
Обратный Быстрое преобразование Фурье может использоваться для эффективного синтеза частот, которые равномерно делят период преобразования или «кадр». Внимательно изучив DFT представление в частотной области также возможно эффективно синтезировать синусоиды произвольных частот, используя серию перекрывающихся кадров и обратного Быстрое преобразование Фурье.[15]
Аддитивный анализ / ресинтез

Можно анализировать частотные составляющие записанного звука, давая представление «сумма синусоид». Это представление может быть повторно синтезировано с помощью аддитивного синтеза. Один из методов разложения звука на изменяющиеся во времени синусоидальные части: кратковременное преобразование Фурье (STFT)-на основе McAulay-Quatieri Анализ.[17][18]
Изменяя сумму представлений синусоид, можно произвести тембральные изменения до ресинтеза. Например, гармонический звук можно преобразовать в негармоничный, и наоборот. Звуковая гибридизация или «морфинг» была осуществлена аддитивным ресинтезом.[19]
Аддитивный анализ / ресинтез использовался в ряде методов, включая синусоидальное моделирование,[20] Синтез спектрального моделирования (SMS),[19] и модель аддитивного звука с переназначенной полосой пропускания.[21] Программное обеспечение, реализующее аддитивный анализ / ресинтез, включает: SPEAR,[22] ЛЕМУР, ЛОРИС,[23] SMSTools,[24] ARSS.[25]
Товары
New England Digital Синклавир имел функцию ресинтеза, где образцы можно было анализировать и преобразовывать в «тембровые кадры», которые были частью его механизма аддитивного синтеза. Технос акксель, запущенная в 1987 году, использовала модель аддитивного анализа / ресинтеза в БПФ выполнение.
Также вокальный синтезатор, Вокалоид были реализованы на основе аддитивного анализа / ресинтеза: его спектральная модель голоса называется Возбуждение плюс резонансы (EpR) модель[26][27] расширен на основе Spectral Modeling Synthesis (SMS), и его дифон конкатенативный синтез обрабатывается с использованиемобработка спектральных пиков (SPP)[28] техника аналогична модифицированной вокодер с фазовой синхронизацией[29] (улучшенный фазовый вокодер для обработки формант).[30] Используя эти методы, спектральные компоненты (форманты), состоящий из чисто гармонических составляющих, может быть соответствующим образом преобразован в желаемую форму для моделирования звука, а последовательность коротких сэмплов (дифоны или же фонемы), составляющие желаемую фразу, могут быть плавно соединены путем интерполяции согласованных частичных и формантных пиков, соответственно, во вставленной переходной области между различными выборками. (Смотрите также Динамические тембры)
Приложения
Музыкальные инструменты
Аддитивный синтез используется в электронных музыкальных инструментах. Это основной метод генерации звука, используемый Выдающийся органы.
Синтез речи
В лингвистика Исследования, гармонический аддитивный синтез был использован в 1950-х годах для воспроизведения модифицированных и синтетических спектрограмм речи.[31]
Позже, в начале 1980-х годов, были проведены тесты на аудирование синтетической речи без акустических сигналов, чтобы оценить их значимость. Изменяющийся во времени формант частоты и амплитуды, полученные кодирование с линейным прогнозированием синтезировались аддитивно в виде свистов чистого тона. Этот метод называется синусоидальный синтез.[32][33] Так же составное синусоидальное моделирование (CSM)[34][35] используется на пении синтез речи функция на Yamaha CX5M (1984), как известно, использовали аналогичный подход, который независимо был разработан в течение 1966–1979 гг.[36][37] Эти методы характеризуются извлечением и перекомпоновкой набора значимых спектральных пиков, соответствующих нескольким резонансным модам, возникающим в полости рта и носа, с точки зрения акустика. Этот принцип также использовался на синтез физического моделирования метод, называемый модальный синтез.[38][39][40][41]
История
Гармонический анализ был обнаружен Жозеф Фурье,[42] опубликовавший обширный трактат о своих исследованиях в контексте теплопередача в 1822 г.[43] Теория нашла раннее применение в предсказание приливов. Около 1876 г.[44] Лорд Кельвин построил механический предсказатель приливов. Он состоял из гармонический анализатор и гармонический синтезатор, как их называли еще в 19 веке.[45][46] Анализ измерений приливов и отливов проводился с использованием Джеймс Томсонс интегрирующая машина. Результирующий Коэффициенты Фурье были введены в синтезатор, который затем использовал систему шнуров и шкивов для генерации и суммирования гармонических синусоидальных частиц для предсказания будущих приливов. В 1910 году аналогичная машина была построена для анализа периодических звуковых сигналов.[47] Синтезатор построил график комбинированного сигнала, который использовался в основном для визуальной проверки анализа.[47]
Георг Ом применил теорию Фурье к звуку в 1843 г. Направление работы было значительно продвинуто Герман фон Гельмгольц, который опубликовал свои восьмилетние исследования в 1863 году.[48] Гельмгольц считал, что психологическое восприятие цвета тона подлежит обучению, в то время как слух в сенсорном смысле является чисто физиологическим.[49] Он поддержал идею о том, что восприятие звука происходит из сигналов от нервных клеток базилярной мембраны и что эластичные придатки этих клеток симпатически вибрируют чистыми синусоидальными тонами соответствующих частот.[47] Гельмгольц согласился с выводом Эрнст Хладни с 1787 года некоторые источники звука имеют негармонические режимы колебаний.[49]
Во времена Гельмгольца электронное усиление был недоступен. Для синтеза тонов с гармоническими частями Гельмгольц построил электрически в восторге массив камертоны и акустический резонансные камеры что позволяло регулировать амплитуды парциальных частиц.[50] Построенный как минимум в 1862 году,[50] они, в свою очередь, были уточнены Рудольф Кениг, который продемонстрировал свою установку в 1872 году.[50] Для гармонического синтеза Кениг также построил большой аппарат на основе своего волновая сирена. Он был пневматическим и имел вырез Tonewheels, и подвергался критике за низкую чистоту полутонов.[44] Также большеберцовые трубы из органы трубы имеют почти синусоидальную форму волны и могут быть объединены способом аддитивного синтеза.[44]
В 1938 году, имея новые важные доказательства,[51] Об этом сообщалось на страницах Ежемесячный научно-популярный журнал что человеческие голосовые связки функционируют как огненная сирена, производя богатый гармониками тон, который затем фильтруется голосовым трактом для получения различных тонов гласных.[52] К тому времени орган Hammond уже был на рынке. Большинство первых производителей электронных органов считали слишком дорогим производство множества генераторов, необходимых для дополнительных органов, и вместо этого начали создавать вычитающий ед.[53] В 1940 г. Институт Радиоинженеров На встрече главный инженер Hammond подробно рассказал о новом Новахорд как имеющий «вычитающая система» в отличие от оригинального органа Hammond, в котором "заключительные тона были созданы путем объединения звуковых волн".[54] Алан Дуглас использовал квалификаторы добавка и вычитающий описать различные типы электронных органов в статье 1948 года, представленной Королевская музыкальная ассоциация.[55] Современная формулировка аддитивный синтез и субтрактивный синтез можно найти в его книге 1957 г. Электрическое производство музыки, в котором категорически перечисляет три метода формирования музыкальных тонов-цветов в разделах, озаглавленных Аддитивный синтез, Субтрактивный синтез, и Другие формы комбинаций.[56]
Типичный современный аддитивный синтезатор выдает свой выходной сигнал как электрические, аналоговый сигнал, или как цифровой звук, например, в случае программные синтезаторы, который стал популярным примерно в 2000 году.[57]
График
Ниже приводится хронология исторически и технологически известных аналоговых и цифровых синтезаторов и устройств, реализующих аддитивный синтез.
| Выполнение или публикация исследования | В продаже | Компания или учреждение | Синтезатор или синтезатор | Описание | Аудио образцы |
|---|---|---|---|---|---|
| 1900[58] | 1906[58] | Музыкальная компания Новой Англии | Телгармониум | Первый полифонический сенсорный музыкальный синтезатор.[59] Реализован синусоидальный аддитивный синтез с использованием Tonewheels и генераторы. Изобретенный Таддеус Кэхилл. | нет известных записей[58] |
| 1933[60] | 1935[60] | Компания Hammond Organ | Hammond Organ | Электронный аддитивный синтезатор, который был коммерчески более успешным, чем Telharmonium.[59] Реализован синусоидальный аддитивный синтез с использованием Tonewheels и магнитные звукосниматели. Изобретенный Лоуренс Хэммонд. | |
| 1950 или ранее[31] | Лаборатории Хаскинса | Воспроизведение паттернов | Система синтеза речи, которая контролировала амплитуды гармонических составляющих с помощью спектрограммы, нарисованной от руки или в результате анализа. Частицы генерировались многодорожечным оптическим Tonewheel.[31] | образцы | |
| 1958[61] | ANS | Аддитивный синтезатор[62] что играл микротональный спектрограмма-подобные партитуры с использованием нескольких многодорожечных оптических Tonewheels. Изобретенный Евгений Мурзин. Аналогичный прибор, использующий электронные генераторы, Осциллятор Банк, и его устройство ввода Спектрограмма были реализованы Хью Ле Кейн в 1959 г.[63][64] | |||
| 1963[65] | Массачусетский технологический институт | Автономная система для цифрового спектрального анализа и ресинтеза атакующих и устойчивых частей тембров музыкальных инструментов Дэвида Люса.[65] | |||
| 1964[66] | Университет Иллинойса | Генератор гармонических тонов | Электронная система гармонического аддитивного синтеза, изобретенная Джеймсом Бошампом.[66][67] | образцы (Информация) | |
| 1974 или ранее[68][69] | 1974[68][69] | RMI | Гармонический синтезатор | Первый синтезатор с добавкой[70] синтез с использованием цифровых генераторов.[68][69] Синтезатор также имел аналоговый фильтр, изменяющийся во времени.[68] RMI была дочерней компанией Компания Аллена Органа, выпустивший первый рекламный ролик цифровой церковный орган, то Компьютерный орган Аллена, в 1971 году с использованием цифровых технологий, разработанных Североамериканский Роквелл.[71] | 1 2 3 4 |
| 1974[72] | EMS (Лондон) | Банк Цифрового Осциллятора | Банк цифровых осцилляторов с произвольной формой сигналов, индивидуальной регулировкой частоты и амплитуды,[73] предназначен для использования в анализе-ресинтезе с цифровым Анализ банка фильтров (AFB) также построено на EMS.[72][73] Также известный как: Дата рождения. | в новом звуке музыки[74] | |
| 1976[75] | 1976[76] | Fairlight | Qasar M8 | Полностью цифровой синтезатор, использующий Быстрое преобразование Фурье[77] для создания сэмплов из интерактивно нарисованных огибающих амплитуд гармоник.[78] | образцы |
| 1977[79] | Bell Labs | Цифровой синтезатор | А в реальном времени, цифровой аддитивный синтезатор[79] его назвали первым настоящим цифровым синтезатором.[80] Также известный как: Аллес машина, Алиса. | образец (Информация) | |
| 1979[80] | 1979[80] | New England Digital | Синклавир II | Коммерческий цифровой синтезатор, который позволил развивать тембр с течением времени за счет плавных переходов между формами волны, генерируемыми аддитивным синтезом. |
Уравнения с дискретным временем
В цифровых реализациях аддитивного синтеза дискретное время уравнения используются вместо уравнений синтеза в непрерывном времени. Условные обозначения для сигналов с дискретным временем используют скобки, т.е. и аргумент могут быть только целочисленные значения. Если выход непрерывного синтеза ожидается, будет достаточно ограниченный диапазон; ниже половины частота выборки или же , достаточно непосредственно выбрать выражение для непрерывного времени, чтобы получить уравнение дискретного синтеза. Выход непрерывного синтеза позже может быть реконструирован из образцов с помощью цифро-аналоговый преобразователь. Период выборки .
Начиная с (3),
и отбор проб в дискретное время приводит к
куда
- - огибающая амплитуды, изменяющаяся в дискретном времени
- дискретное время обратная разница мгновенная частота.
Это эквивалентно
куда
- для всех [15]
и
Смотрите также
Рекомендации
- ^ а б Юлий О. Смит III. «Аддитивный синтез (раннее синусоидальное моделирование)». Получено 14 января 2012.
Термин «аддитивный синтез» относится к звуку, который формируется путем сложения множества синусоидальных компонентов.
- ^ Гордон Рид. "Секреты синтеза, часть 14: Введение в аддитивный синтез". Звук на звуке (Январь 2000 г.). Получено 14 января 2012.
- ^ Моттола, Лютайо (31 мая 2017 г.). «Таблица музыкальных нот, их частоты и длины волны».
- ^ «Основная частота и гармоники».
- ^ Смит III, Юлий О .; Серра, Ксавье (2005). «Аддитивный синтез». PARSHL: программа анализа / синтеза негармонических звуков, основанная на синусоидальном представлении. Труды Международной конференции компьютерной музыки (ICMC-87, Токио), Ассоциация компьютерной музыки, 1987. CCRMA, Факультет музыки Стэнфордского университета. Получено 11 января 2015. (онлайн-перепечатка)
- ^ Смит III, Джулиус О. (2011). «Аддитивный синтез (раннее синусоидальное моделирование)». Спектральная обработка аудиосигнала. CCRMA, Факультет музыки Стэнфордского университета. ISBN 978-0-9745607-3-1. Получено 9 января 2012.
- ^ Дороги, Кертис (1995). Учебник компьютерной музыки. MIT Press. п.134. ISBN 978-0-262-68082-0.
- ^ а б Мур, Ф. Ричард (1995). Основы компьютерной музыки. Prentice Hall. п. 16. ISBN 978-0-262-68082-0.
- ^ Дороги, Кертис (1995). Учебник компьютерной музыки. MIT Press. стр.150–153. ISBN 978-0-262-68082-0.
- ^ Роберт Бристоу-Джонсон (ноябрь 1996 г.). "Синтез волновой таблицы 101, фундаментальная перспектива" (PDF). Архивировано из оригинал (PDF) 15 июня 2013 г.. Получено 21 мая 2005.
- ^ Эндрю Хорнер (ноябрь 1995 г.). "Волновая таблица согласования синтеза динамических инструментов с генетическими алгоритмами". Журнал Общества звукорежиссеров. 43 (11): 916–931.
- ^ Юлий О. Смит III. «Групповой аддитивный синтез». CCRMA, Стэндфордский Университет. В архиве из оригинала от 6 июня 2011 г.. Получено 12 мая 2011.
- ^ П. Клечковский (1989). «Групповой аддитивный синтез». Компьютерный музыкальный журнал. 13 (1): 12–20. Дои:10.2307/3679851. JSTOR 3679851.
- ^ Б. Иглстоун и С. Оутс (1990). «Аналитические инструменты для группового аддитивного синтеза». Материалы Международной компьютерной музыкальной конференции 1990 г., Глазго. Ассоциация компьютерной музыки.
- ^ а б Rodet, X .; Депалле, П. (1992). «Огибающие спектра и обратный синтез БПФ». Труды 93-го съезда Аудиотехнического общества. CiteSeerX 10.1.1.43.4818.
- ^ McAulay, R.J .; Кватири, Т.Ф. (1988). «Обработка речи на основе синусоидальной модели» (PDF). Журнал лаборатории Линкольна. 1 (2): 153–167. Архивировано из оригинал (PDF) 21 мая 2012 г.. Получено 9 декабря 2013.
- ^ McAulay, R.J .; Quatieri, T. F. (август 1986). «Анализ / синтез речи на основе синусоидального представления». Транзакции IEEE по акустике, речи и обработке сигналов ASSP-34. 34 (4): 744–754. Дои:10.1109 / ТАССП.1986.1164910.
- ^ «Метод Маколея-Кватиери».
- ^ а б Серра, Ксавьер (1989). Система звукового анализа / преобразования / синтеза на основе детерминированной и стохастической декомпозиции (Кандидатская диссертация). Стэндфордский Университет. Получено 13 января 2012.
- ^ Смит III, Юлий О .; Серра, Ксавьер. "PARSHL: Программа анализа / синтеза негармонических звуков, основанная на синусоидальном представлении". Получено 9 января 2012.
- ^ Фитц, Келли (1999). Метод аддитивного синтеза с переназначенной полосой пропускания (Кандидатская диссертация). Кафедра электротехники и вычислительной техники, Иллинойский университет в Урбана-Шампейн. CiteSeerX 10.1.1.10.1130.
- ^ Анализ синусоидального частичного редактирования и ресинтез SPEAR для Mac OS X, MacOS 9 и Windows
- ^ «Программное обеспечение Loris для моделирования звука, морфинга и манипуляции». Архивировано из оригинал 30 июля 2012 г.. Получено 13 января 2012.
- ^ Приложение SMSTools для Windows
- ^ ARSS: спектрограф звука для анализа и ресинтеза
- ^ Bonada, J .; Celma, O .; Loscos, A .; Ортола, Дж .; Серра, X .; Yoshioka, Y .; Kayama, H .; Hisaminato, Y .; Кенмочи, Х. (2001). «Синтез певческого голоса, сочетающий возбуждение плюс резонанс и синусоидальную плюс остаточную модели». Proc. ICMC. CiteSeerX 10.1.1.18.6258. (PDF)
- ^ Лоскос, А. (2007). Спектральная обработка певческого голоса (Кандидатская диссертация). Барселона, Испания: Университет Помпеу Фабра. HDL:10803/7542. (PDF).
Видеть "Модель голоса Возбуждение плюс резонанс"(стр. 51) - ^ Loscos 2007, п. 44, "Обработка спектральных пиков »
- ^ Loscos 2007, п. 44, "Вокодер с фазовой синхронизацией"
- ^ Бонада, Хорди; Лоскос, Алекс (2003). «Основанный на сэмплах синтезатор певческого голоса путем спектральной конкатенации: 6. Конкатенация сэмплов». Proc. из SMAC 03: 439–442.
- ^ а б c Купер, Ф. С .; Либерман, А. М .; Борст, Дж. М. (май 1951 г.). «Взаимопревращение звуковых и визуальных образов как основа для исследования восприятия речи». Proc. Natl. Акад. Sci. СОЕДИНЕННЫЕ ШТАТЫ АМЕРИКИ. 37 (5): 318–25. Bibcode:1951ПНАС ... 37..318С. Дои:10.1073 / pnas.37.5.318. ЧВК 1063363. PMID 14834156.
- ^ Remez, R.E .; Рубин, П.Е .; Pisoni, D.B .; Каррелл, Т. Д. (1981). «Восприятие речи без традиционных речевых сигналов». Наука. 212 (4497): 947–950. Bibcode:1981Научный ... 212..947R. Дои:10.1126 / science.7233191. PMID 7233191. S2CID 13039853.
- ^ Рубин, П. (1980). "Руководство по синтезу синусоидальной волны (VAX)" (PDF). Внутренний меморандум. Лаборатории Хаскинса, Нью-Хейвен, Коннектикут.
- ^ Сагаяма, С.; Итакура, Ф. (1979), «複合 正弦波 に よ る 音 声» [синтез речи с помощью составной синусоидальной волны], Речь Комитета Акустического Общества Японии (опубликовано в октябре 1979 г.), S79-39
- ^ Sagayama, S .; Итакура, Ф. (1979), «複合 正弦波 に よ る 簡易 な 音 声 合成» [Метод простого синтеза речи с помощью составной синусоидальной волны], Труды Японского акустического общества, осеннее собрание (опубликовано в октябре 1979 г.), 3-2-3, стр. 557–558.
- ^ Sagayama, S .; Итакура, Ф. (1986). «Теория двойственности составного синусоидального моделирования и линейного предсказания». ICASSP '86. Международная конференция IEEE по акустике, речи и обработке сигналов. Акустика, речь и обработка сигналов, Международная конференция IEEE по ICASSP '86. 11 (опубликовано в апреле 1986 г.). С. 1261–1264. Дои:10.1109 / ICASSP.1986.1168815. S2CID 122814777.
- ^ Итакура, Ф. (2004). «Линейное статистическое моделирование речи и его приложения - более 36 лет истории LPC -» (PDF). Труды 18-го Международного конгресса по акустике (ICA 2004), We3.D, Киото, Япония, апрель 2004 г. (опубликовано в апреле 2004 г.). 3: III – 2077–2082.
6. Составное синусоидальное моделирование (CSM) В 1975 году Итакура предложил концепцию линейчатого представления спектра (LSR) и ее алгоритм для получения набора параметров для нового представления спектра речи. Независимо от этого, Сагаяма разработал концепцию составного синусоидального моделирования (CSM), которая эквивалентна LSR, но дает совершенно иную формулировку, алгоритм решения и схему синтеза. Сагаяма разъяснил двойственность LPC и CSM и представил единое представление, охватывающее LPC, PARCOR, LSR, LSP и CSM, CSM - это не только новая концепция анализа спектра речи, но и ключевая идея для понимания линейного прогнозирования с единой точки зрения. Посмотреть. ...
- ^ Адриан, Жан-Мари (1991). «Недостающее звено: модальный синтез». В Джованни де Поли; Альдо Пиччиалли; Curtis Roads (ред.). Представления музыкальных сигналов. Кембридж, Массачусетс: MIT Press. стр.269–298. ISBN 978-0-262-04113-3.
- ^ Моррисон, Джозеф Дерек (IRCAM); Адриан, Жан-Мари (1993). «МОЗАИКА: структура для модального синтеза». Компьютерный музыкальный журнал. 17 (1): 45–56. Дои:10.2307/3680569. JSTOR 3680569.
- ^ Бильбао, Стефан (октябрь 2009 г.), «Модальный синтез», Численный синтез звука: конечно-разностные схемы и моделирование в музыкальной акустике, Чичестер, Великобритания: Джон Уайли и сыновья, ISBN 978-0-470-51046-9,
Другой подход, долгое время использовавшийся при физическом моделировании синтеза звука, основан на частотном или модальном описании вибрации объектов потенциально сложной геометрии. Модальный синтез [1,148], как его называют, привлекателен тем, что сложное динамическое поведение вибрирующего объекта может быть разложено на вклады от набора мод (пространственные формы которых являются собственными функциями конкретной рассматриваемой проблемы, и зависят от граничных условий), каждое из которых колеблется с одной комплексной частотой. ...
(Смотрите также сопутствующая страница) - ^ Доэль, Кейс ван ден; Пай, Динеш К. (2003). Гринебаум, К. (ред.). «Модальный синтез для вибрирующего объекта» (PDF). Аудио анекдоты. Натик, Массачусетс: AK Питер.
Когда твердый объект ударяется, царапается или участвует в других внешних взаимодействиях, силы в точке контакта вызывают деформации, распространяющиеся по телу, заставляя его внешние поверхности вибрировать и излучать звуковые волны. ... Хорошей физически мотивированной моделью синтеза для подобных объектов является модальный синтез ... где вибрирующий объект моделируется набором затухающих гармонических осцилляторов, которые возбуждаются внешним стимулом.
- ^ Престини, Елена (2004) [Rev. изд: Applicazioni dell'analisi armonica. Милан: Ульрико Хёпли, 1996]. Эволюция прикладного гармонического анализа: модели реального мира. пер. Нью-Йорк, США: Birkhäuser Boston. С. 114–115. ISBN 978-0-8176-4125-2. Получено 6 февраля 2012.
- ^ Фурье, Жан Батист Жозеф (1822). Теория аналитик де ля шалёр [Аналитическая теория тепла] (На французском). Париж, Франция: Chez Firmin Didot, père et fils.
- ^ а б c Миллер, Дейтон Кларенс (1926) [Впервые опубликовано в 1916 году]. Наука о музыкальных звуках. Нью-Йорк: Компания Macmillan. стр.110, 244–248.
- ^ Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал. Тейлор и Фрэнсис. 49: 490. 1875.CS1 maint: журнал без названия (связь)
- ^ Томсон, сэр У. (1878). «Гармонический анализатор». Труды Лондонского королевского общества. Тейлор и Фрэнсис. 27 (185–189): 371–373. Дои:10.1098 / rspl.1878.0062. JSTOR 113690.
- ^ а б c Кахан, Дэвид (1993). Кахан, Дэвид (ред.). Герман фон Гельмгольц и основы науки XIX века. Беркли и Лос-Анджелес, США: Калифорнийский университет Press. С. 110–114, 285–286. ISBN 978-0-520-08334-9.
- ^ Гельмгольц, фон, Герман (1863). Die Lehre von den Tonempfindungen как Physiologische Grundlage für die Theorie der Musik [Об ощущениях тона как физиологической основе теории музыки] (на немецком языке) (1-е изд.). Лейпциг: Леопольд Восс. стр. v.
- ^ а б Кристенсен, Томас-стрит (2002). Кембриджская история западной музыки. Кембридж, Соединенное Королевство: Издательство Кембриджского университета. С. 251, 258. ISBN 978-0-521-62371-1.
- ^ а б c фон Гельмгольц, Герман (1875). Об ощущениях тона как физиологической основе теории музыки. Лондон, Соединенное Королевство: Longmans, Green, and co. С. xii, 175–179.
- ^ Рассел, Джордж Оскар (1936). Ежегодник - Вашингтонский институт Карнеги (1936). Вашингтонский институт Карнеги: Ежегодник. 35. Вашингтон: Вашингтонский институт Карнеги. стр.359–363.
- ^ Лодж, Джон Э. (апрель 1938 г.). Браун, Раймонд Дж. (Ред.). «Странные лабораторные тесты показывают нам, как мы говорим: с помощью рентгеновских лучей, быстрых кинокамер и электронно-лучевых трубок ученые изучают новые факты о человеческом голосе и разрабатывают методы обучения, которые сделают нас лучше говорящими». Ежемесячный научно-популярный журнал. Нью-Йорк, США: Popular Science Publishing. 132 (4): 32–33.
- ^ Комерфорд, П. (1993). «Моделирование органа с помощью аддитивного синтеза». Компьютерный музыкальный журнал. 17 (2): 55–65. Дои:10.2307/3680869. JSTOR 3680869.
- ^ "Новости института и радио-заметки". Труды IRE. 28 (10): 487–494. 1940. Дои:10.1109 / JRPROC.1940.228904.
- ^ Дуглас, А. (1948). «Электротонная музыка». Труды Королевской музыкальной ассоциации. 75: 1–12. Дои:10.1093 / jrma / 75.1.1.
- ^ Дуглас, Алан Локхарт Монтейт (1957). Электрическое производство музыки. Лондон, Великобритания: Макдональд. стр.140, 142.
- ^ Пейроло, Андреа; ДеРоса, Рич (2007). Акустическая и MIDI оркестровка для современного композитора. Оксфорд, Великобритания: Эльзевир. С. 53–54.
- ^ а б c Weidenaar, Рейнольд (1995). Волшебная музыка из Телгармониума. Лэнхэм, Мэриленд: Scarecrow Press. ISBN 978-0-8108-2692-2.
- ^ а б Муг, Роберт А. (октябрь – ноябрь 1977 г.). "Электронная музыка". Журнал Общества звукорежиссеров. 25 (10/11): 856.
- ^ а б Олсен, Харви (14 декабря 2011 г.). Браун, Даррен Т. (ред.). «Лесли Спикерс и органы Хаммонда: слухи, мифы, факты и знания». Зона Хаммонд. Орган Hammond в Великобритании. оригинал 1 сентября 2012 г.. Получено 20 января 2012.
- ^ Хольцер, Дерек (22 февраля 2010 г.). «Краткая история оптического синтеза». Получено 13 января 2012.
- ^ Вейл, Марк (1 ноября 2002 г.). "АНС Евгения Мурзина - Аддитивный русский синтезатор". Журнал Keyboard. п. 120.
- ^ Янг, Гейл. «Осцилляторный банк (1959)».
- ^ Янг, Гейл. «Спектрограмма (1959)».
- ^ а б Люс, Дэвид Алан (1963). Физические корреляты звуков ударных музыкальных инструментов (Тезис). Кембридж, Массачусетс, США: Массачусетский технологический институт. HDL:1721.1/27450.
- ^ а б Бошан, Джеймс (17 ноября 2009 г.). "Генератор гармонических тонов: один из первых аналоговых синтезаторов, управляемых напряжением". Домашняя страница профессора Джеймса В. Бошампа.
- ^ Бошан, Джеймс У. (октябрь 1966 г.). «Аддитивный синтез гармонических музыкальных тонов». Журнал Общества звукорежиссеров. 14 (4): 332–342.
- ^ а б c d "Гармонический синтезатор RMI". Synthmuseum.com. В архиве из оригинала от 9 июня 2011 г.. Получено 12 мая 2011.
- ^ а б c Рид, Гордон. "PROG SPAWN! Взлет и падение инструментов Rocky Mount (ретро)". Звук на звуке (Декабрь 2001 г.). Архивировано из оригинал 25 декабря 2011 г.. Получено 22 января 2012.
- ^ Флинт, Том. "Жан Мишель Жарр: 30 лет кислородного голодания". Звук на звуке (Февраль 2008 г.). Получено 22 января 2012.
- ^ "Компания Аллен Орган". financialuniverse.com.
- ^ а б Козими, Энрико (20 мая 2009 г.). «EMS Story - Prima Parte» [История EMS - Часть первая]. Аудио Accordo.it (на итальянском). Архивировано из оригинал 22 мая 2009 г.. Получено 21 января 2012.
- ^ а б Хинтон, Грэм (2002). "EMS: Внутренняя история". Студии электронной музыки (Корнуолл). Архивировано из оригинал 21 мая 2013 г.
- ^ Новое звучание музыки (ТЕЛЕВИДЕНИЕ). ВЕЛИКОБРИТАНИЯ: BBC. 1979 г. Включает демонстрацию DOB и AFB.
- ^ Лите, Норм. "Fairlight Computer - Музыкальный инструмент (Ретро)". Звук на звуке (Апрель 1999 г.). Получено 29 января 2012.
- ^ Твайман, Джон (1 ноября 2004 г.). (между) лицом к музыке: История компьютерного музыкального инструмента Fairlight (PDF) (Диплом бакалавра наук (с отличием)). Отдел истории и философии науки, Сиднейский университет. Получено 29 января 2012.
- ^ Улица, Рита (8 ноября 2000 г.). "Fairlight: 25-летняя сказка". Журнал Audio Media. IMAS Publishing UK. Архивировано из оригинал 8 октября 2003 г.. Получено 29 января 2012.
- ^ "Компьютерный музыкальный журнал" (JPG). 1978. Получено 29 января 2012.
- ^ а б Лейдер, Колби (2004). «Развитие современного DAW». Цифровая аудио рабочая станция. Макгроу-Хилл. п. 58.
- ^ а б c Джоэл, Чадаб (1997). Электрический звук. Река Аппер Сэдл, Нью-Джерси, США: Prentice Hall. С. 177–178, 186. ISBN 978-0-13-303231-4.







![{ begin {align} y (t) & = { frac {a_ {0}} {2}} + sum _ {k = 1} ^ { infty} left [a_ {k} cos (2 pi kf_ {0} t) -b_ {k} sin (2 pi kf_ {0} t) right] & = { frac {a_ {0}} {2}} + sum _ { k = 1} ^ { infty} r_ {k} cos left (2 pi kf_ {0} t + phi _ {k} right) конец {выровнено}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/522ace082a6d8990934113a639987f09a885cf02)




























![у [п] ,](https://wikimedia.org/api/rest_v1/media/math/render/svg/e73a8042c0d1a4c5d264982972d2ef33eda55e34)





![{ begin {align} y [n] & = y (nT) = sum _ {k = 1} ^ {K} r_ {k} (nT) cos left (2 pi int _ {0} ^ {nT} f_ {k} (u) du + phi _ {k} right) & = sum _ {k = 1} ^ {K} r_ {k} (nT) cos left ( 2 pi sum _ {i = 1} ^ {n} int _ {(i-1) T} ^ {iT} f_ {k} (u) du + phi _ {k} right) & = sum _ {k = 1} ^ {K} r_ {k} (nT) cos left (2 pi sum _ {i = 1} ^ {n} (Tf_ {k} [i]) + phi _ {k} right) & = sum _ {k = 1} ^ {K} r_ {k} [n] cos left ({ frac {2 pi} {f _ { mathrm {s}}}} sum _ {i = 1} ^ {n} f_ {k} [i] + phi _ {k} right) конец {выровнено}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/235e423ed6dcd7564ba02d91eee3b6a012e84ce4)
![r_ {k} [n] = r_ {k} (nT) ,](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a91ccc3b0935394fad361cdc119c27a51b0c278)
![f_ {k} [n] = { frac {1} {T}} int _ {(n-1) T} ^ {nT} f_ {k} (t) dt ,](https://wikimedia.org/api/rest_v1/media/math/render/svg/1043b3eaee212fedc8c9c8d408aad44dce3c4af1)
![y [n] = sum _ {k = 1} ^ {K} r_ {k} [n] cos left ( theta _ {k} [n] right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbce88acb5e1e6a4ef32dd0be9bd49b78325a7de)
![{ begin {align} theta _ {k} [n] & = { frac {2 pi} {f _ { mathrm {s}}}} sum _ {i = 1} ^ {n} f_ { k} [i] + phi _ {k} & = theta _ {k} [n-1] + { frac {2 pi} {f _ { mathrm {s}}}} f_ {k } [п] конец {выровнено}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9b7b0acccac5e1f4c4d5739654caf234277411e)

![theta _ {k} [0] = phi _ {k}. ,](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea1d7745c11e8890b24efb6c72f8c5a320d8b27e)