WikiDer > Угловой блок
Было предложено, чтобы эта статья была слился в Угол № Измерение. (Обсуждать) Предлагается с мая 2020 года. |
На протяжении всей истории, углы Был измеренный во многих разных единицы. Они известны как угловые единицы, причем самыми современными единицами являются степень (°), радиан (рад), а Градиан (град), хотя многие другие использовались повсюду история.[1][2] Цель этой страницы - обобщить другие концепции, относящиеся к угловая единица, где могут быть даны дополнительные пояснения.
Измерение углов в целом
Размер геометрического угла обычно характеризуется величиной наименьшего поворота, который переводит один из лучей в другой. Углы одинакового размера называются равный, конгруэнтный или же равны по мере.
В некоторых контекстах, таких как определение точки на круге или описание ориентация объекта в двух измерениях относительно исходной ориентации, углы, которые различаются точным числом, кратным полному повернуть эффективно эквивалентны. В других контекстах, таких как определение точки на спираль кривая, или описывающая совокупное вращение объекта в двух измерениях относительно исходной ориентации, углы, которые различаются ненулевым кратным полному обороту, не эквивалентны.
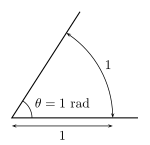
Чтобы измерить угол θ, а дуга окружности с центром в вершине угла (например, с помощью пары компасы). Соотношение длины s дуги на радиус р круга - это мера угла в радианы.
Затем значение угла в другой угловой единице получается путем умножения его измерения в радианах на коэффициент масштабирования. k/2π, куда k - мера полного оборота в выбранной единице (например, 360 для градусы или 400 для грады):
Значение θ определенное таким образом, не зависит от размера круга: если длина радиуса изменяется, то длина дуги изменяется в той же пропорции, поэтому соотношение s/р без изменений. (Доказательство. Формулу выше можно переписать как k = θr/s. Один оборот, за который θ = п единиц, соответствует дуге, равной длине окружности длина окружности, что составляет 2πр, так s = 2πр. Подстановка п за θ и 2πр за s в формуле приводит к k = номер/2πр = п/2π.) [nb 1]
В частности, мера угла в радианах может также интерпретироваться как длина дуги соответствующей единичной окружности:[4]
Постулат сложения углов
Постулат сложения углов утверждает, что если B находится внутри угла AOC, то
Мера угла AOC - это сумма меры угла AOB и меры угла BOC. В этом постулате не имеет значения, в каком единица измерения угол измеряется до тех пор, пока каждый угол измеряется в одной и той же единице.
Единицы
Один радиан - угол, образованный дугой окружности, длина которой равна радиусу окружности. Радиан - это производная величина углового измерения в SI система. По определению это безразмерный, хотя его можно указать как рад чтобы избежать двусмысленности. Углы измеряются в градусы, обозначены символом °. Подразделения степени: минута (символ ′, 1 ′ = 1/60 °) и второй {символ ″, 1 ″ = 1/3600 °}.[1] Угол 360 ° соответствует углу, образуемому полным кругом, и равен 2π радианам или 400 градусам.
Другие единицы измерения углов перечислены в следующей таблице. Эти единицы определены таким образом, что количество повороты эквивалентен полному кругу.
| имя | повороты | угол поворота | описание |
|---|---|---|---|
| Повернуть | 1 | 360° | В повернуть, также цикл, полный круг, революция, и вращение, представляет собой полное круговое движение или измерение (чтобы вернуться в ту же точку) с помощью круга или эллипса. Оборот сокращен τ, цикл, rev, или же гнить в зависимости от применения .. Символ τ также может использоваться как математическая константа представлять 2π радианы. |
| Кратные π | 2 | 180° | В кратные π (MULπ) реализован в РПН научный калькулятор WP 43S.[5][6][7] Смотрите также: Рекомендуемые операции IEEE 754 |
| Квадрант | 4 | 90° | Один квадрант также известен как прямой угол. Квадрант - это единица измерения, используемая в Элементы Евклида. На немецком языке символ ∟ использовался для обозначения квадранта. |
| Секстант | 6 | 60° | В секстант была единица, используемая Вавилоняне,[8][9] Градус, угловая минута и секунда дуги являются шестидесятеричный подразделения вавилонского отряда. Особенно легко строить с помощью линейки и циркуля. |
| Радиан | 2π | 57°17′ | В радиан определяется длиной окружности, равной радиусу окружности. |
| Гексаконтада | 60 | 6° | В гексаконтада единица, используемая Эратосфен. |
| Бинарная степень | 256 | 1°33'45" | В двоичная степень, также известный как двоичный радиан (или же Брэд).[10] Двоичная степень используется в вычислениях, так что угол может быть эффективно представлен в одном байт (хотя и с ограниченной точностью). Другие меры угла, используемые в вычислениях, могут быть основаны на делении одного целого поворота на 2.п равные части для других значений п. |
| Степень | 360 | 1° | Одно из преимуществ этого старого шестидесятеричный Подразделение состоит в том, что многие углы, общие для простой геометрии, измеряются как целое число градусов. Доли градуса могут быть записаны в обычной десятичной системе счисления (например, 3,5 ° для трех с половиной градусов), но также используются шестидесятеричные единицы «минута» и «секунда» системы «градус-минута-секунда», особенно за географические координаты И в астрономия и баллистика |
| Град | 400 | 0°54′ | В град, также называемый оценка, Градиан, или же гон. прямой угол - 100 градусов. Это десятичная единица квадранта. А километр исторически определялся как санти-градиент дуги по меридиан Земли, поэтому километр является десятичным аналогом шестидесятеричный морская миля. Град используется в основном в триангуляция. |
| Угловая минута | 21,600 | 0°1′ | В угловая минута (или же MOA, угловая минута, или просто минута) является 1/60 степени. А морская миля исторически определялся как угловая минута вдоль большой круг земли. |
| Секунда дуги | 1,296,000 | 0°0′1″ | В секунда дуги (или же угловая секунда, или просто второй) является 1/60 угловой минуты и 1/3600 степени. |
Эквивалентные дескрипторы времени
В астрономия, прямое восхождение и склонение обычно измеряются в угловых единицах, выраженных в единицах времени, исходя из 24-часового дня.
| Единица измерения | Символ | Степень | Радианы | Круг | Другой |
|---|---|---|---|---|---|
| Час | час | 15° | π⁄12 | 1⁄24 | |
| Минуты | м | 0°15' | π⁄720 | 1⁄1,440 | 1⁄60 час |
| Второй | s | 0°0'15" | π⁄43200 | 1⁄86,400 | 1⁄60 минута |
Другие дескрипторы
- Тау, количество радианов в одном повернуть (1 оборот = τ рад), τ = 2π.
- Чи, старое китайское измерение угла.[нужна цитата]
- Часть диаметра (п = 376,99 ...): часть диаметра (иногда используется в исламской математике) 1/60 радиан. Одна «часть диаметра» составляет приблизительно 0,95493 °. На оборот приходится около 376,991 деталей диаметром.
- Миллирадский и производные определения: Истинный миллирадиан определяется одной тысячной радиана, что означает, что поворот на одну повернуть будет равняться точно 2000π мил (или приблизительно 6283,185 мил), и почти все прицелы за огнестрельное оружие откалиброваны под это определение. Кроме того, есть три других производных определения, используемых для артиллерии и навигации, которые примерно равняется миллирадиану. Согласно этим трем другим определениям, один оборот составляет ровно 6000, 6300 или 6400 мил, что соответствует диапазону от 0,05625 до 0,06 градусов (от 3,375 до 3,6 минут). Для сравнения, истинный миллирадиан составляет приблизительно 0,05729578 градуса (3,43775 минуты). Один "НАТО mil "определяется как 1/6400 круга. Как и в случае с истинным миллирадианом, каждое из других определений использует полезное свойство миллирадиана субтензий, то есть то, что значение одного миллирадиана приблизительно равно углу, образуемому шириной 1 метр, если смотреть с расстояния 1 км (2π/6400 = 0.0009817… ≈ 1/1000).
- Ахнам и зам. В старой Аравии повернуть был разделен на 32 акнама, и каждый ахнам был подразделен на 7 зам, так что повернуть 224 зам.
Положительные и отрицательные углы
Хотя определение измерения угла не поддерживает концепцию отрицательного угла, часто бывает полезно наложить соглашение, которое позволяет положительным и отрицательным угловым значениям представлять ориентацию и повороты в противоположных направлениях относительно некоторой ссылки.
В двухмерном Декартова система координат, угол обычно определяется двумя его сторонами с вершиной в начале координат. В начальная сторона на позитиве ось абсцисс, а другая сторона (т.е. сторона терминала) определяется мерой от начальной стороны в радианах, градусах или оборотах. Обычно положительные углы представляют поворот к положительному ось Y, и отрицательные углы представляют повороты к отрицательной оси y. Когда декартовы координаты представлены стандартное положение, определяемый осью x вправо и осью y вверх, положительные повороты против часовой стрелки, а отрицательные повороты равны по часовой стрелке.
Во многих контекстах угол -θ фактически эквивалентен углу "один полный оборот минус θ". Например, ориентация, представленная как -45 °, фактически эквивалентна ориентации, представленной как 360 ° - 45 ° или 315 °. Однако поворот на -45 ° не будет таким же, как поворот на 315 °.
В трехмерной геометрии «по часовой стрелке» и «против часовой стрелки» не имеют абсолютного значения, поэтому направление положительных и отрицательных углов должно быть определено относительно некоторой ссылки, которая обычно является вектор проходящая через вершину угла и перпендикулярная плоскости, в которой лежат лучи угла.
В навигация, подшипники измеряются относительно севера. Условно, если смотреть сверху, угол пеленга положительный по часовой стрелке, поэтому пеленг 45 ° соответствует ориентации на северо-восток. Отрицательные пеленги не используются в навигации, поэтому ориентация на северо-запад соответствует пеленгу 315 °.
Альтернативные способы измерения размера угла
Существует несколько альтернатив измерению размера угла соответствующим углом поворота. уклон склона, или же градиент, равно касательная угла или иногда (редко) синус. Градиенты часто выражаются в процентах. Для очень малых значений (менее 5%) крутизна наклона приблизительно равна величине угла в радианах.
В рациональная геометрия, то распространять между двумя линиями определяется как квадрат синуса угла между линиями. Поскольку синус угла и синус его дополнительного угла одинаковы, любой угол поворота, который отображает одну из линий в другую, приводит к одинаковому значению разброса между линиями.
Астрономические приближения
Астрономы измеряют угловое расстояние между объектами в градусах от точки наблюдения.
- 0,5 ° - это примерно ширина солнца или луны.
- 1 ° - это примерно ширина мизинца на расстоянии вытянутой руки.
- 10 ° - это примерно ширина сжатого кулака на расстоянии вытянутой руки.
- 20 ° - это примерно ширина размаха рук на расстоянии вытянутой руки.
Эти измерения явно зависят от конкретного объекта, и все вышеизложенное следует рассматривать как грубые. практическое правило только приближения.
Измерения, не являющиеся угловыми единицами
Не все угловые измерения являются угловыми единицами, для углового измерения определением является постулат сложения углов держит.
Некоторые угловые измерения, когда постулат сложения углов не включает:
Примечания
- ^ Однако этот подход требует дополнительного доказательства того, что величина угла не меняется с изменением радиуса. р, помимо вопроса «выбранных единиц измерения». Более плавный подход состоит в том, чтобы измерить угол по длине соответствующей дуги единичной окружности. Здесь «единица» может быть выбрана безразмерной в том смысле, что это действительное число 1, связанное с единичным сегментом на реальной линии. См., Например, Радослав М. Димитрич.[3]
Смотрите также
Рекомендации
- ^ а б «Список символов геометрии и тригонометрии». Математическое хранилище. 2020-04-17. Получено 2020-08-31.
- ^ «угловая единица». TheFreeDictionary.com. Получено 2020-08-31.
- ^ Димитрич, Радослав М. (2012). «Об углах и угловых измерениях» (PDF). Обучение математике. XV (2): 133–140. В архиве (PDF) из оригинала на 17.01.2019. Получено 2019-08-06.
- ^ Вайсштейн, Эрик В. "Радиан". mathworld.wolfram.com. Получено 2020-08-31.
- ^ Бонин, Уолтер (11 января 2016). «RE: WP-32S в 2016 году?». Музей HP. В архиве из оригинала на 2019-08-06. Получено 2019-08-05.
- ^ Бонин, Вальтер (2019) [2015]. WP 43S Руководство пользователя (PDF). 0,12 (черновик ред.). С. 72, 118–119, 311. ISBN 978-1-72950098-9. ISBN 1-72950098-6. Получено 2019-08-05.[постоянная мертвая ссылка] [1] [2] (314 стр.)
- ^ Бонин, Вальтер (2019) [2015]. Справочное руководство WP 43S (PDF). 0,12 (черновик ред.). С. III, 54, 97, 128, 144, 193, 195. ISBN 978-1-72950106-1. ISBN 1-72950106-0. Получено 2019-08-05.[постоянная мертвая ссылка] [3] [4] (271 стр.)
- ^ Джинсы, Джеймс Хопвуд (1947). Рост физической науки. КУБОК Архив. п.7.
- ^ Мурнаган, Фрэнсис Доминик (1946). Аналитическая геометрия. п. 2.
- ^ "Руководство программиста ooPIC - Глава 15: URCP". ooPIC Руководство и технические характеристики - компилятор ooPIC, версия 6.0. Savage Innovations, ООО. 2007 [1997]. Архивировано из оригинал на 2008-06-28. Получено 2019-08-05.
- ^ Харгривз, Шон. «Углы, целые числа и арифметика по модулю». blogs.msdn.com. В архиве из оригинала на 2019-06-30. Получено 2019-08-05.