WikiDer > Шайба Бельвиль

Belleville washer

Шайба Бельвиль

А Шайба Бельвиль, также известный как конусно-дисковая пружина,^[1] коническая пружинная шайба,^[2] дисковая пружина, Бельвильская весна или же чашечная пружинная шайба, представляет собой коническую оболочку, которая может нагружаться вдоль своей оси статически или динамически. Стиральная машина Бельвиль - это разновидность весна в форме Шайба. Это разочарование-конический форма, придающая шайбе характерную пружину.

Название «Бельвиль» происходит от изобретателя Жюльен Бельвиль кто в Дюнкерк, Франция, в 1867 г. запатентовала конструкцию пружины, которая уже содержала принцип тарельчатой пружины.^[1]^[3] Настоящий изобретатель шайб Belleville неизвестен.

За прошедшие годы было разработано множество профилей для дисковых пружин. Сегодня наиболее часто используются профили с контактными лесками или без них, тогда как некоторые другие профили, например, дисковые пружины с трапециевидным поперечным сечением, потеряли свое значение.

Особенности и использование

Поперечный разрез Противотанковая мина М4 (около 1945 г.) демонстрирует стальную тарельчатую пружину в взрыватель механизм

Вид в разрезе Противопехотная мина М14, показывая ударник установлен в центре пластиковой тарельчатой пружины

В различных полях, если они используются в качестве пружин или для приложения гибкой предварительной нагрузки к болтовое соединение или подшипник, шайбы Бельвилля могут использоваться как одна пружина или как набор. В пакете пружин тарельчатые пружины могут быть уложены стопкой в одной или в чередующейся ориентации, и, конечно, можно уложить пакеты из нескольких пружин, уложенных в одном направлении.

Дисковые пружины обладают рядом преимуществ по сравнению с другими типами пружин:^[4]

Очень большие нагрузки могут поддерживаться при небольшом пространстве для установки,
Благодаря практически неограниченному количеству возможных комбинаций отдельных тарельчатых пружин характеристическая кривая и длина стойки могут быть изменены в дополнительных пределах.
Большой срок службы при динамической нагрузке при правильном выборе размеров пружины,
Если допустимое напряжение не превышено, недопустимой релаксации не происходит,
При соответствующем расположении может быть достигнут большой эффект демпфирования (высокий гистерезис),
Поскольку пружины имеют кольцевую форму, передача усилия абсолютно концентрическая.

Благодаря этим выгодным свойствам, шайбы Belleville сегодня используются в большом количестве областей, некоторые примеры перечислены ниже.

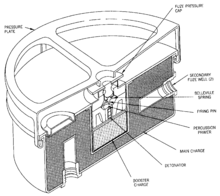
В оружейной промышленности пружины Бельвилля используются, например, в ряде наземные мины например Американец M19, M15, M14, M1 и шведский Tret-Mi.59. Цель (человек или транспортное средство) оказывает давление на тарельчатую пружину, в результате чего она превысит порог срабатывания и перевернет соседний ударник вниз в удар детонатор, стреляя как в него, так и в окружающих подзарядка и основное взрывчатое наполнение.

Шайбы Belleville использовались в качестве возвратных пружин в артиллерийские орудияОдним из примеров является французская дальность морской / береговой пушки Canet с конца 1800-х годов (75 мм, 120 мм, 152 мм).

Некоторые производители затвор В винтовках-мишенях используются стопки шайб Бельвилля в затворе вместо более традиционной пружины для освобождения ударника, так как они сокращают время между срабатыванием спускового крючка и ударом ударника по патрону.^[5]

Шайбы Belleville без зубцов, которые могут повредить зажимную поверхность, не обладают значительной блокирующей способностью при использовании болтов. ^[6]

На самолетах (обычно экспериментальных самолетах) с деревянными винтами шайбы Бельвилля, используемые на крепежных болтах, могут быть полезны в качестве индикатора разбухания или усадки древесины. Затягивая соответствующие болты, чтобы обеспечить определенный зазор между наборами шайб, размещенных так, чтобы «высокие концы» были обращены друг к другу, изменение относительного содержания влаги в дереве пропеллера приведет к изменению зазоров, которые часто достаточно велики, чтобы их можно было обнаружить. визуально. Поскольку балансировка гребного винта зависит от веса лопастей, которые равны, радикальное различие в зазоре под шайбу может указывать на разницу в содержании влаги и, следовательно, в весе соседних лопастей.

В авиационной и автомобильной промышленности (в том числе Формула один легковые автомобили^[7]) тарельчатые пружины используются в качестве элементов гашения вибрации из-за их чрезвычайно точной настройки. В самолетах серии Cirrus SR2x используется шайба Бельвилля для демпфирования. передняя стойка колебания (или «шимми»).^[8]

В строительстве в Японии наборы дисковых пружин использовались под зданиями в качестве гасителей вибрации при землетрясениях.^[9]

Штабелирование

Несколько шайб Бельвилля могут быть установлены друг на друга, чтобы изменить жесткость пружины (или пружинная ставка) или количество отклонение. Укладка в одном направлении добавит жесткость пружины параллельно, создавая более жесткое соединение (с таким же прогибом). Укладка в чередующемся направлении аналогична последовательному добавлению общих пружин, что приводит к более низкой жесткости пружины и большему прогибу. Направления смешивания и согласования позволяют рассчитать конкретную жесткость пружины и прогибающую способность.

Обычно, если п тарельчатые пружины уложены параллельно (в одном направлении), выдерживая нагрузку, прогиб всего пакета равен прогибу одной тарельчатой пружины, разделенной на п, то для получения такого же прогиба одинарной тарельчатой пружины прикладываемая нагрузка должна быть п раз больше, чем у однодисковой пружины. С другой стороны, если п шайбы уложены последовательно (обращены в чередующиеся стороны), выдерживая нагрузку, прогиб равен п раз больше, чем у одной шайбы, в то время как нагрузка, прилагаемая ко всему пакету для получения такого же прогиба одной тарельчатой пружины, должна быть такой же, как у одиночной тарельчатой пружины, разделенной на п.

Соображения производительности

В параллельном пакете будет возникать гистерезис (потери нагрузки) из-за трения между пружинами. Гистерезисные потери могут быть полезны в некоторых системах из-за дополнительного демпфирования и рассеивания энергии колебаний. Эти потери из-за трения можно рассчитать с помощью методов гистерезиса. В идеале следует размещать параллельно не более 4 пружин. Если требуется большая нагрузка, необходимо увеличить запас прочности, чтобы компенсировать потерю нагрузки из-за трения. Потери на трение не так важны для серийных стеков

В последовательном стеке прогиб не совсем пропорционален количеству пружин. Это из-за дно эффект, когда пружины сжаты до плоского состояния, поскольку площадь контактной поверхности увеличивается, когда пружина отклоняется более чем на 95%. Это уменьшает плечо момента, и пружина будет обеспечивать большее сопротивление пружины. Гистерезис можно использовать для расчета прогнозируемых прогибов в последовательном сумме. Количество пружин, используемых в последовательном стопке, не является такой большой проблемой, как в параллельных пакетах, даже если, как правило, высота стопки не должна превышать трехкратный внешний диаметр тарельчатой пружины. Если невозможно избежать более длинной стопки, ее следует разделить на 2 или, возможно, 3 частичных стопки с подходящими шайбами. Эти шайбы следует направлять как можно точнее.

Как уже говорилось ранее, шайбы Бельвилля полезны для регулировки, потому что их можно менять местами разной толщины, и их можно настроить для достижения практически неограниченной регулировки жесткости пружины, заполняя только небольшую часть ящика для инструментов техника. Они идеальны в ситуациях, когда требуется большая сила пружины с минимальной свободной длиной и сжатием до достижения твердой высоты. Обратной стороной является вес, и они сильно ограничены в перемещении по сравнению с обычной винтовой пружиной, когда свободная длина не является проблемой.

А волнообразная шайба также действует как пружина, но волнообразные шайбы сопоставимого размера не создают такой силы, как шайбы Бельвилля, и их нельзя складывать последовательно.

Тарельчатые пружины с плоскими контактами и уменьшенной толщиной

Для тарельчатых пружин толщиной более 6,0 мм DIN 2093 определяет малые контактные поверхности в точках I и III (это точка приложения нагрузки и точка, где нагрузка касается земли) в дополнение к закругленным углам. Эти контактные поверхности улучшают определение точки приложения нагрузки и, особенно для пружинных пакетов, уменьшают трение на направляющем стержне. Результат - значительное уменьшение длины плеча рычага и соответствующее увеличение нагрузки пружины. Это, в свою очередь, компенсируется уменьшением толщины пружины.

Уменьшенная толщина указана в соответствии со следующими условиями:^[4]

Общая высота остается неизменной,
Ширина контактных поверхностей (то есть ширина кольцевого пространства) должна составлять примерно 1/150 внешнего диаметра.
Нагрузка, прикладываемая к пружине уменьшенной толщины для получения прогиба, равного 75% свободной высоты (неусаженной пружины), должна быть такой же, как и для неусаженной пружины.

Поскольку общая высота не уменьшается, пружины с уменьшенной толщиной неизбежно имеют увеличенный угол наклона боковой поверхности и большую высоту конуса, чем пружины того же номинального размера без уменьшения толщины.^[4] Поэтому характеристическая кривая изменяется и становится совершенно другой.

Расчет

Начиная с 1936 г., когда J.O. Almen и A.Làszlò опубликовали упрощенный метод расчета,^[10] всегда появлялись более точные и сложные методы включения в расчеты тарельчатых пружин с плоскими контактами и уменьшенной толщиной. Итак, хотя сегодня существуют более точные методы расчета,^[11] Чаще всего используются простые и удобные формулы DIN 2092, поскольку для стандартных размеров они дают значения, которые хорошо соответствуют результатам измерений.

С учетом шайбы Бельвилля с наружным диаметром ${ displaystyle {D_ {e}}}$ , Внутренний диаметр ${ displaystyle {D_ {i}}}$ , высота ${ displaystyle {l}}$ и толщина ${ displaystyle {t}}$ , куда ${ displaystyle {h_ {0}}}$ - свободная высота, то есть разница между высотой и толщиной, получаются следующие коэффициенты:

{ displaystyle delta = { frac {D_ {e}} {D_ {i}}}}

{ displaystyle {C_ {1}} = { frac { left ({ frac {t '} {t}} right) ^ {2}} { left ({ frac {1} {4}}) cdot { frac {l} {t}} - { frac {t '} {t}} + { frac {3} {4}} right) cdot { left ({ frac {5} {8}} cdot { frac {l} {t}} - { frac {t '} {t}} + { frac {3} {8}} right)}}}}

{ displaystyle {C_ {2}} = { frac {C_ {1}} { left ({ frac {t '} {t}} right) ^ {3}}} cdot left [{ гидроразрыв {5} {32}} cdot left ({ frac {l} {t}} - 1 right) ^ {2} +1 right]}

{ displaystyle {K_ {4}} = { sqrt {- { frac {C_ {1}} {2}} + { sqrt { left ({ frac {C_ {1}} {2}} вправо) ^ {2} + C_ {2}}}}}}

Уравнение для расчета нагрузки, прилагаемой к однодисковой пружине, чтобы получить прогиб ${ displaystyle {s}}$ является:^[12]

{ displaystyle F = { frac {4E} {1- mu ^ {2}}} cdot { frac {t ^ {4}} {K_ {1} - {D_ {e}} ^ {2} }} cdot {K_ {4}} ^ {2} cdot { frac {s} {t}} cdot left [{K_ {4}} ^ {2} cdot left ({ frac { h_ {0}} {t}} - { frac {s} {t}} right) cdot left ({ frac {h_ {0}} {t}} - { frac {s} {2t }} right) +1 right]}

Обратите внимание, что для тарельчатых пружин постоянной толщины ${ displaystyle {t '}}$ равно ${ displaystyle {t}}$ и следовательно ${ displaystyle {K_ {4}}}$ равно 1.

Что касается тарельчатых пружин с плоскими контактами и уменьшенной толщиной, следует отметить, что статья, опубликованная в июле 2013 года, продемонстрировала, что ${ displaystyle {K_ {4}}}$ Уравнение, как определено в стандартных нормах, неверно, так как в результате каждая уменьшенная толщина будет считаться правильной, а это, конечно, невозможно. Как написано в этой статье ${ displaystyle {K_ {4}}}$ следует заменить на новый коэффициент, ${ displaystyle {R_ {d}}}$ , что зависит не только от ${ displaystyle { frac {t '} {t}}}$ отношение, но и от боковых углов пружины.^[13]

Жесткость пружины (или жесткость пружины) определяется как:

{ displaystyle {k} = { frac {dF} {ds}}}

Иллюстрация стека шайб Belleville

Если пренебречь эффектами трения и дна, жесткость пружины набора идентичных шайб Бельвилля может быть быстро вычислена. Отсчитывая от одного конца стопки, сгруппируйте по количеству соседних шайб, расположенных параллельно. Например, в стопке шайб справа группировка будет 2-3-1-2, потому что есть группа из 2 шайб параллельно, затем группа из 3, затем одна шайба, затем еще одна группа из 2 .

Общий коэффициент пружины составляет:

{ Displaystyle К = { гидроразрыва {k} { сумма _ {я = 1} ^ {g} { гидроразрыва {1} {n_ {i}}}}}}

{ displaystyle K = { frac {k} {{ frac {1} {2}} + { frac {1} {3}} + { frac {1} {1}} + { frac {1} } {2}}}}}

{ Displaystyle К = { гидроразрыва {3} {7}} cdot {k}}

Где

${ displaystyle n_ {i}}$ = количество шайб в i-й группе
${ displaystyle {g}}$ = количество групп
${ displaystyle {k}}$ = жесткость пружины одной шайбы

Таким образом, стопка 2-3-1-2 (или, поскольку сложение коммутативно, стопка 3-2-2-1) дает жесткость пружины 3/7 жесткости одиночной шайбы. Эти же 8 шайб можно расположить по схеме 3-3-2 ( ${ Displaystyle К = { гидроразрыва {6} {7}} cdot k}$ ), конфигурация 4-4 ( ${ Displaystyle К = 2 cdot k}$ ), конфигурация 2-2-2-2 ( ${ Displaystyle К = { гидроразрыва {1} {2}} cdot}$ ) и различные другие конфигурации. Количество уникальных способов укладки ${ displaystyle {n}}$ шайбы определяется целочисленная статистическая сумма п(п) и быстро увеличивается с большими ${ displaystyle {n}}$ , позволяя точно настраивать жесткость пружины. Однако каждая конфигурация будет иметь разную длину, что потребует использования прокладки в большинстве случаев.

Стандарты

DIN EN 16983 ранее DIN 2092 - Тарельчатые пружины - Расчет
DIN EN 16984 ранее DIN 2093 - Тарельчатые пружины - Характеристики производства и качества^[14]
DIN 6796 - Шайбы конические пружинные для болтовых соединений^[2]

Navigation