WikiDer > Самолет Benz

Benz plane

В математика, а Самолет Benz это тип 2-размерный геометрический структура, названная в честь Немецкий математик Уолтер Бенц. Термин применялся к группе объектов, которые возникают из общего аксиоматизация определенных структур и разделились на три семейства, которые были введены отдельно: Самолеты Мебиуса, Самолеты Лагерра, и Самолеты Минковского.^[1]^[2]

Самолет Мебиуса

классический самолет Мёбиуса: 2d / 3d модель

Начиная с настоящий Евклидова плоскость и объединение набора линий с набором кругов для формирования набора блоков приводит к неоднородному структура заболеваемости: три различных точки определяют один блок, но линии различимы как набор блоков, которые попарно взаимно пересекаться в одной точке без касания (или без точек при параллельности). Добавление к точке устанавливает новую точку ${displaystyle infty}$ , определенная как лежащая на каждой прямой, приводит к тому, что каждый блок определяется ровно тремя точками, а также пересечением любых двух блоков по единому шаблону (пересекающимся в двух точках, касательным или непересекающимся). Эта однородная геометрия называется классической инверсивной геометрией или плоскостью Мёбиуса. Неоднородность описания (линии, круги, новая точка) можно рассматривать как несущественную, используя трехмерную модель. Используя стереографическая проекция, можно видеть, что классическая плоскость Мёбиуса изоморфна геометрии плоские сечения (кружки) на сфере в трехмерном евклидовом пространстве.

Аналогично (аксиоматике) проективная плоскость, (аксиоматическая) плоскость Мёбиуса определяет структуру инцидентности. Аналогичным образом можно построить плоскости Мебиуса над поля кроме реальных чисел.

Самолет Лагерра

классический самолет Лагерра: 2d / 3d-модель

Начиная снова с ${displaystyle extstyle mathbb {R} ^ {2}}$ и взяв кривые с уравнениями ${displaystyle y = ax ^ {2} + bx + c}$ (параболы и линии) в виде блоков эффективна следующая гомогенизация: Добавить к кривой ${displaystyle y = ax ^ {2} + bx + c}$ новая точка ${displaystyle (infty, a)}$ . Следовательно, набор точек равен ${displaystyle (mathbb {R} чашка {infty}) imes mathbb {R}}$ . Эта геометрия парабол называется классической плоскостью Лагерра (изначально она была задумана как геометрия ориентированных прямых и окружностей. Обе геометрии изоморфны).

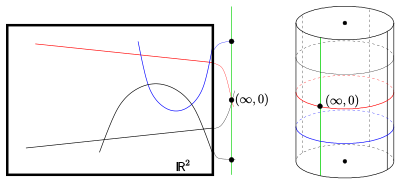
Что касается плоскости Мебиуса, существует 3-мерная модель: геометрия эллиптических плоских сечений на ортогональном цилиндре (в ${displaystyle mathbb {R} ^ {3}}$ ). Абстракция ведет (аналогично плоскости Мёбиуса) к аксиоматической плоскости Лагерра.

Самолет Минковского

классический самолет Минковского: 2d / 3d-модель

Начиная с ${displaystyle mathbb {R} ^ {2}}$ и слияние строк ${displaystyle y = mx + d, meq 0}$ с гиперболами ${displaystyle y = {frac {a} {x-b}} + c, aeq 0}$ Чтобы получить набор блоков, следующая идея гомогенизирует структуру инцидентности: Добавьте к любой строке точку ${displaystyle (infty, infty)}$ и к любой гиперболе ${displaystyle y = {frac {a} {x-b}} + c, aeq 0}$ две точки ${displaystyle (b, infty), (infty, c)}$ . Следовательно, набор точек равен ${displaystyle (mathbb {R} чашка {infty}) ^ {2}}$ . Эта геометрия гипербол называется классической плоскостью Минковского.

Аналогично классическим плоскостям Мёбиуса и Лагерра существует 3-мерная модель: классическая плоскость Минковского изоморфна геометрии плоских сечений гиперболоида одного листа (невырожденная квадрика индекса 2) в 3-мерном проективном пространстве. Как и в первых двух случаях, мы получаем (аксиоматическую) плоскость Минковского.

Плоские окружности или плоскости Бенца

Из-за существенной роли круга (рассматриваемого как невырожденный конический в проективная плоскость) и плоское описание исходных моделей, три типа геометрии относятся к геометрии плоского круга или в честь Уолтера Бенца, который рассматривал эти геометрические структуры с общей точки зрения, плоскости Бенца.

Смотрите также

внешняя ссылка

[1] В. Бенц, Vorlesungen über Geomerie der Algebren, Springer (1973)

[2] Ф. Бюкенхаут (ред.), Справочник по Геометрия падения, Эльзевир (1995) ISBN 0-444-88355-X

[1]

[2]

Navigation