WikiDer > Пересечение
Эта статья нужны дополнительные цитаты для проверка. (Январь 2014) (Узнайте, как и когда удалить этот шаблон сообщения) |
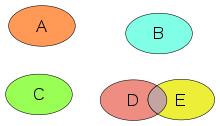
В математика, то пересечение из двух или более объектов - это другой, обычно «меньший» объект. Предполагается, что все объекты лежат в определенной общей Космос кроме теория множеств, где определено пересечение произвольных множеств. Перекресток - одно из основных понятий геометрия. Интуитивно понятно, что пересечение двух или более объекты - это новый объект, который лежит в каждом из исходных объектов. Перекресток может иметь разные геометрические фигуры, но точка является наиболее распространенным в плоская геометрия.
Определения различаются в зависимости от контекста: теория множеств формализует идею о том, что меньший объект лежит в большом объекте с включение, а пересечение множеств состоит из элементы принадлежащие всем пересекающимся множествам. Это всегда определенный, но возможно пустой. Геометрия падения определяет пересечение (обычно квартиры) как объект нижнего измерение то есть инцидент каждому из оригинальных предметов. При таком подходе пересечение иногда может быть неопределенным, например, для параллельные линии. В обоих случаях концепция пересечения опирается на логическое соединение.
Алгебраическая геометрия определяет пересечения по-своему с теория пересечений.Евклидова геометрия имеет дело с пересечениями плоских и твердых форм.
Уникальность
Может быть несколько примитивных объектов, таких как точки (на фото выше), которые образуют пересечение. Пересечение можно рассматривать вместе как все общие объекты (т. Е. Перекресток операция приводит к набор, возможно, пустой), или как несколько объектов пересечения (возможно ноль).
В теории множеств
Пересечение двух множеств А и B это набор элементов, которые находятся в обоих А и B. В символах
- .[1]
Например, если А = {1, 3, 5, 7} и B = {1, 2, 4, 6}, тогда А ∩ B = {1}. Более сложный пример (включающий бесконечные множества):
- А = {Икс это даже целое число}
- B = {Икс целое число, делящееся на 3}
Другой пример: цифра 5 - это нет содержащиеся в пересечении множества простые числа {2, 3, 5, 7, 11,…} и набор четные числа {2, 4, 6, 8, 10,…}, потому что хотя 5 является простое число, это нет четное. Фактически, число 2 - единственное число на пересечении этих двух множеств. В этом случае пересечение имеет математический смысл: число 2 - единственное четное простое число.
В евклидовой геометрии
- Линия – пересечение линии
- Пересечение прямой и плоскости
- Пересечение линии и сферы
- Пересечение многогранника линией
- Пересечение отрезка прямой
- Кривая пересечения
Обозначение
Пересечение обозначается U + 2229 ∩ ПЕРЕСЕЧЕНИЕ из Математические операторы Unicode.
Эта секция нуждается в расширении с: история символа. Вы можете помочь добавляя к этому. (Январь 2014) |
Символ U + 2229 ∩ впервые был использован Герман Грассманн в Die Ausdehnungslehre von 1844 как общий символ операции, не предназначенный для перекрестков. Оттуда он использовался Джузеппе Пеано (1858-1932) для перекрестка, в 1888 г. Calcolo geometryo secondo l'Ausdehnungslehre di H. Grassmann.[2][3]
Джузеппе Пеано также создал большие символы для общего пересечения и объединения более двух классов в 1908 году в своей книге Formulario mathematico.[4][5]
Смотрите также
- Конструктивная твердотельная геометрия, Boolean Intersection - один из способов комбинирования 2D / 3D фигур.
- Размерно расширенная модель с 9 пересечениями
- Знакомьтесь (теория решетки)
Рекомендации
- ^ Верещагин Николай Константинович; Шен, Александр (01.01.2002). Основная теория множеств. American Mathematical Soc. ISBN 9780821827314.
- ^ Пеано, Джузеппе (1888-01-01). Calcolo geometryo secondo l'Ausdehnungslehre di H. Grassmann: Preduto dalle operazioni della logica deduttiva (на итальянском). Турин: Fratelli Bocca.
- ^ Каджори, Флориан (01.01.2007). История математических обозначений. Турин: Cosimo, Inc. ISBN 9781602067141.
- ^ Пеано, Джузеппе (1908-01-01). Formulario mathematico, Томо V (на итальянском). Турин: Edizione cremonese (Перепечатка факсов в Риме, 1960). п. 82. OCLC 23485397.
- ^ Самые ранние случаи использования символов теории множеств и логики




