WikiDer > Куб Бидьякиса
| Куб Бидьякиса | |
|---|---|
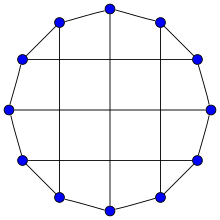 Куб Бидьякиса | |
| Вершины | 12 |
| Края | 18 |
| Радиус | 3 |
| Диаметр | 3 |
| Обхват | 4 |
| Автоморфизмы | 8 (D4) |
| Хроматическое число | 3 |
| Хроматический индекс | 3 |
| Характеристики | Кубический Гамильтониан Без треугольников Многогранник Планарный |
| Таблица графиков и параметров | |
в математический поле теория графов, то Куб Бидьякиса это 3-регулярный граф с 12 вершинами и 18 ребрами.[1]
Строительство
Куб Бидиакиса - это кубический Гамильтонов граф и может быть определена Обозначение LCF [-6,4,-4]4.
Куб Бидиакиса также можно построить из куба, добавив ребра через верхнюю и нижнюю грани, которые соединяют центры противоположных сторон граней. Два дополнительных края должны быть перпендикулярны друг другу. При такой конструкции куб Бидиакиса представляет собой многогранный граф, и может быть реализована как выпуклый многогранник. Следовательно, по Теорема Стейница, это 3-вершинно-связанный просто планарный граф.[2][3]
Алгебраические свойства
Куб Бидиакиса - это не вершинно-транзитивный граф и его полная группа автоморфизмов изоморфна группе группа диэдра порядка 8 группа симметрий квадрат, включая как вращения, так и отражения.
В характеристический многочлен куба Бидиакиса .
Галерея
В хроматическое число куба Бидиакиса равно 3.
В хроматический индекс куба Бидиакиса равно 3.
Куб Бидиакиса - это планарный граф.
Куб Бидиакиса, построенный из куба.
Рекомендации
- ^ Вайсштейн, Эрик В. "Куб Бидьякиса". MathWorld.
- ^ Бранко Грюнбаум, Выпуклые многогранники, 2-е издание, подготовлено Фолькер Кайбель, Виктор Клее, и Гюнтер М. Циглер, 2003, ISBN 0-387-40409-0, ISBN 978-0-387-40409-7, 466с.
- ^ Вайсштейн, Эрик В. «Многогранный граф». MathWorld.