WikiDer > Тепловая машина Карно - Википедия
Эта статья нужны дополнительные цитаты для проверка. (Октябрь 2018 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |

А Тепловой двигатель Карно[2] теоретический двигатель, работающий на Цикл Карно. Базовая модель этого двигателя была разработана Николя Леонар Сади Карно в 1824 году. Модель двигателя Карно была графически расширена Бенуа Поль Эмиль Клапейрон в 1834 г. и математически исследовал Рудольф Клаузиус в 1857 году работа, которая привела к фундаментальной термодинамической концепции энтропия.
Каждая термодинамическая система существует в определенном государственный. А термодинамический цикл происходит, когда система проходит через серию различных состояний и, наконец, возвращается в исходное состояние. В процессе прохождения этого цикла система может выполнять работу со своим окружением, тем самым действуя как Тепловой двигатель.
Тепловой двигатель действует, передавая энергию из теплой области в прохладную область пространства и, в процессе, преобразуя часть этой энергии в механическая работа. Цикл также может быть обратным. На систему может воздействовать внешняя сила, и в процессе она может передавать тепловую энергию от более холодной системы к более теплой, тем самым действуя как холодильник или же Тепловой насос а не тепловой двигатель.
Диаграмма Карно
На соседней диаграмме из работы Карно 1824 г. Размышления о движущей силе огня,[3] есть "два тела" А и B, держали каждый при постоянной температуре, А быть выше, чем у B. Эти два тела, которым мы можем отдавать или от которых мы можем отводить тепло, не изменяя их температуру, выполняют функции двух неограниченных резервуаров калорийность. Мы будем называть первый печь а второй - холодильник ».[4] Затем Карно объясняет, как мы можем получить сила мотивации, т. е. «работать», отводя определенное количество тепла от тела А к телу B.Он также действует как охладитель и, следовательно, может также действовать как холодильник.
Современная диаграмма

На предыдущем изображении показана оригинальная диаграмма поршня и цилиндра, которую Карно использовал при обсуждении своих идеальных двигателей. На рисунке справа показана блок-схема типового теплового двигателя, такого как двигатель Карно. На схеме «рабочее тело» (система), термин, введенный Клаузиусом в 1850 году, может быть любым жидким или паровым телом, через которое высокая температура Q могут быть представлены или переданы для производства работы. Карно постулировал, что жидким телом может быть любое вещество, способное к расширению, такое как пары воды, пары спирта, пары ртути, постоянный газ или воздух и т. Д. Хотя в те ранние годы двигатели появились в большом количестве. конфигураций, обычно QЧАС снабжался котлом, в котором воду кипятили над топкой; QC обычно подавался потоком холодной текущей воды в виде конденсатор расположен на отдельной части двигателя. Выходная работа, W, представляет собой движение поршня, поскольку он используется для поворота кривошипа, который, в свою очередь, обычно использовался для привода шкива, чтобы поднимать воду из затопленных соляных шахт. Карно определил работу как «поднятие тяжестей на высоту».
Цикл Карно
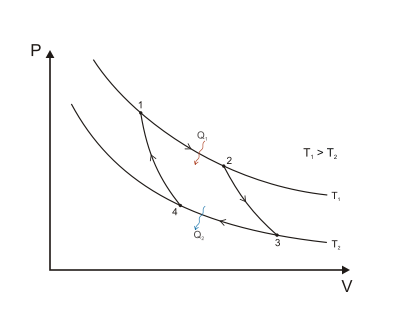
В Цикл Карно при работе в качестве тепловой машины состоит из следующих этапов:
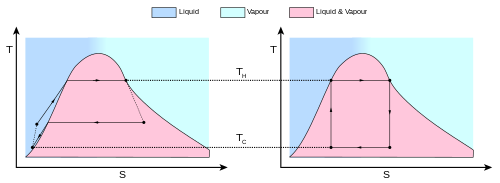
- Обратимый изотермический расширение газа при «горячей» температуре, ТЧАС (изотермическое добавление или поглощение тепла). На этом этапе (1-2 на рисунке 1, А к B на рисунке 2) газу позволяют расширяться, и он действует на окружающую среду. Температура газа не изменяется во время процесса, поэтому расширение является изотермическим. Расширение газа происходит за счет поглощения тепловой энергии. Q1 и энтропии из высокотемпературного резервуара.
- Изэнтропический (обратимая адиабатическая) расширение газа (выход изоэнтропической работы). Для этого шага (2–3 на рис. 1, B к C на Рисунке 2) предполагается, что поршень и цилиндр имеют теплоизоляцию, поэтому они не получают и не теряют тепло. Газ продолжает расширяться, воздействуя на окружающую среду и теряя эквивалентное количество внутренней энергии. Расширение газа заставляет его охлаждаться до «холодной» температуры, ТC. Энтропия остается неизменной.
- Обратимое изотермическое сжатие газа при «холодной» температуре, ТC. (отвод изотермического тепла) (3-4 на рисунке 1, C к D на рисунке 2) Теперь газ подвергается воздействию холодного температурного резервуара, в то время как окружающая среда воздействует на газ, сжимая его (например, посредством обратного сжатия поршня), вызывая при этом некоторое количество тепловой энергии. Q2 и энтропии стечь из газа в низкотемпературный резервуар. (Это такое же количество энтропии, поглощенное на этапе 1.) Эта работа меньше, чем работа, выполняемая с окружающей средой на этапе 1, потому что она происходит при более низком давлении, учитывая отвод тепла в холодный резервуар, когда происходит сжатие (т. Е. сопротивление сжатию ниже на этапе 3, чем сила расширения на этапе 1).
- Изэнтропическое сжатие газа (ввод изэнтропической работы). (4 к 1 на Рисунке 1, D к А на рис. 2). Опять же предполагается, что поршень и цилиндр имеют теплоизоляцию, а резервуар с холодной температурой удален. Во время этого этапа окружающая среда продолжает работать над дальнейшим сжатием газа, при этом температура и давление повышаются теперь, когда радиатор удален. Эта дополнительная работа увеличивает внутреннюю энергию газа, сжимая его и вызывая повышение температуры до ТЧАС. Энтропия остается неизменной. В этот момент газ находится в том же состоянии, что и в начале шага 1.
Теорема Карно
Теорема Карно является формальным утверждением этого факта: Ни один двигатель, работающий между двумя тепловыми резервуарами, не может быть более эффективным, чем двигатель Карно, работающий между одними и теми же резервуарами.
(1)
Объяснение
Эта максимальная эффективность определяется, как указано выше:
- W это работа, выполняемая системой (энергия, выходящая из системы как работа),
- тепло, поступающее в систему (тепловая энергия, поступающая в систему),
- это абсолютная температура холодного резервуара, и
- это абсолютная температура горячего резервуара.
Следствие теоремы Карно утверждает, что: Все реверсивные двигатели, работающие между одними и теми же тепловыми резервуарами, одинаково эффективны.
Легко показать, что эффективность η максимальна, когда весь циклический процесс является обратимый процесс. Это означает общую энтропия чистой системы (энтропии горячей печи, «рабочего тела» теплового двигателя и холодного стока) остаются постоянными, когда «рабочее тело» завершает один цикл и возвращается в исходное состояние. (В общем случае полная энтропия этой комбинированной системы увеличилась бы в общем необратимом процессе).
Поскольку «рабочая жидкость» возвращается в то же состояние после одного цикла, а энтропия системы является функцией состояния; изменение энтропии системы «рабочая жидкость» равно 0. Таким образом, это означает, что полное изменение энтропии печи и приемника равно нулю, чтобы процесс был обратимым, а эффективность двигателя была максимальной. Этот вывод проводится в следующем разделе.
В коэффициент производительности (COP) теплового двигателя обратно пропорциональна его эффективности.
КПД реальных тепловых машин
Для настоящего теплового двигателя полный термодинамический процесс обычно необратим. Рабочая жидкость возвращается в исходное состояние после одного цикла, и, таким образом, изменение энтропии жидкой системы равно 0, но сумма изменений энтропии в горячем и холодном резервуаре в этом циклическом процессе больше 0.
Внутренняя энергия жидкости также является переменной состояния, поэтому ее полное изменение за один цикл равно 0. Таким образом, общая работа, выполняемая системой. W, равна теплу, подводимому к системе минус выносимое тепло .
(2)
Для реальных двигателей - разделы 1 и 3 цикла Карно; в котором тепло поглощается «рабочей жидкостью» из горячего резервуара и передается им соответственно в холодный резервуар; больше не остаются идеально обратимыми, и существует разница температур между температурой резервуара и температурой жидкости во время теплообмена.
При передаче тепла от горячего резервуара при к жидкости, жидкость будет иметь немного более низкую температуру, чем , и процесс для жидкости не обязательно может оставаться изотермическим. Позволять быть полным изменением энтропии жидкости в процессе приема тепла.
(3)
где температура жидкости Т всегда немного меньше чем , в этом процессе.
Итак, получится
(4)
Точно так же во время закачки тепла из текучей среды в холодный резервуар для величины изменения общей энтропии жидкости в процессе отвода тепла:
- ,
(5)
где во время этого процесса передачи тепла к холодному резервуару температура жидкости Т всегда немного больше, чем .
Мы рассмотрели здесь только величину изменения энтропии. Поскольку полное изменение энтропии жидкостной системы для циклического процесса равно 0, мы должны иметь
(6)
Предыдущие три уравнения в совокупности дают:
(7)
Уравнения (2) и (7) объединить, чтобы дать
(8)
Следовательно,
(9)
куда - КПД реального двигателя, а - КПД двигателя Карно, работающего между одними и теми же двумя резервуарами при температурах и . Для двигателя Карно весь процесс является обратимым, и уравнение (7) является равенством.
Следовательно, эффективность реального двигателя всегда ниже, чем у идеального двигателя Карно.
Уравнение (7) означает, что полная энтропия всей системы (два резервуара + жидкость) увеличивается для реального двигателя, потому что прирост энтропии холодного резервуара как втекает в него при фиксированной температуре , больше, чем потеря энтропии горячего резервуара, поскольку оставляет его при фиксированной температуре . Неравенство в уравнении (7) по сути является утверждением Теорема Клаузиуса.
Согласно второй теореме «КПД двигателя Карно не зависит от природы рабочего тела».
Примечания
- ^ Рисунок 1 у Карно (1824, с. 17) и Карно (1890, с. 63). На схеме диаметр сосуда достаточно велик, чтобы перекрыть пространство между двумя телами, но в модели сосуд никогда не контактирует с обоими телами одновременно. Кроме того, на схеме показан осевой шток без маркировки, прикрепленный к поршню снаружи.
- ^ Во французском Карно использует машина à feu, который Терстон переводит как Тепловой двигатель или же паровой двигатель. В сноске Карно выделяет паровую машину (машина à vapeur) от теплового двигателя в целом. (Карно, 1824, с. 5 и Карно, 1890, с. 43)
- ^ Иногда переводится как Размышления о движущей силе тепла
- ^ Английский перевод Терстона (Карно, 1890, стр. 51-52).
Рекомендации
- Карно, Сади (1824). Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance (На французском). Париж: Башелье. (Издание первое 1824 г.) и (Переиздание 1878 г.)
- Карно, Сади (1890). Терстон, Роберт Генри (ред.). Размышления о движущей силе тепла и машинах, способных развивать эту силу. Нью-Йорк: J. Wiley & Sons. (полный текст 1897 г. изд.) (Архивная HTML-версия)



















