WikiDer > Составная кривая Безье

Composite Bézier curve

Безьергон - красный безьергон проходит через синие вершины, зеленые точки являются контрольными точками, которые определяют форму соединяющихся кривых Безье.

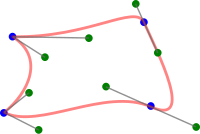
В геометрическое моделирование И в компьютерная графика, а составная кривая Безье кусочно Кривая Безье это по крайней мере непрерывный. Другими словами, составная кривая Безье - это серия кривых Безье, соединенных конец в конец, где последняя точка одной кривой совпадает с начальной точкой следующей кривой. В зависимости от приложения могут быть добавлены дополнительные требования к гладкости (например, непрерывность C1 или C2).^[1]

Непрерывный составной Безье также называется полибезье, по сходству с ломаная линия, но в то время как в полилиниях точки соединяются прямыми линиями, в полибезье точки соединяются кривыми Безье. А Безьергон (также называемый Безигон) - замкнутый путь, состоящий из Кривые Безье. Это похоже на многоугольник в том, что он соединяет набор вершины линиями, но если в многоугольниках вершины соединяются прямыми линиями, то в безьергоне вершины соединяются кривыми Безье.^[2]^[3]^[4] Некоторые авторы даже называют составную кривую Безье C0 «сплайном Безье»;^[5] последний термин, однако, используется другими авторами как синоним (несоставной) кривой Безье, и они добавляют слово «составной» перед «сплайном Безье» для обозначения составного случая.^[6]

Возможно, наиболее частым использованием составного Безье является описание контура каждой буквы в PostScript или PDF файл. Такие очертания состоят из одного безьергона для открытые письма, или несколько безьергонов для закрытых писем. Современное векторная графика и компьютерный шрифт такие системы, как PostScript, Асимптота, Метафонт, OpenType, и SVG используйте составные кривые Безье, состоящие из кубических кривых Безье (кривые 3-го порядка) для рисования изогнутых форм.

Sinc функция, аппроксимированная с помощью гладкого сплайна Безье, то есть серии гладко соединенных кривых Безье

Плавное соединение

Составные кривые Безье можно сглаживать до любой желаемой степени гладкость используя конструкцию Штэрка.^[7]

C2 непрерывные составные кубические кривые Безье на самом деле кубические B-шлицы,^[8] и наоборот.^[9]

Отдельные кривые по определению непрерывны C1 и C2. Геометрическим условием непрерывности C1 при переходе через конечную точку, соединяющую две кривые, является то, что связанные контрольные точки взаимно противоположны и коллинеарен с конечной точкой. Геометрическим условием непрерывности C2 является непрерывность C1 с дополнительным ограничением, что контрольные точки эквидистантны от конечной точки.

Аппроксимирующие дуги окружности

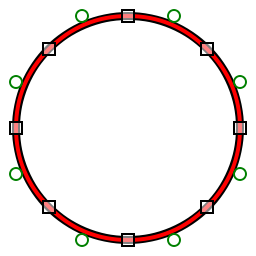
В случае, если примитивы дуги окружности не поддерживаются в конкретной среде, они могут быть аппроксимированы Кривые Безье.^[10] Обычно восемь квадратичных сегментов^[11] или четыре кубических сегмента используются для аппроксимации круга. Желательно подобрать длину ${ displaystyle mathbf {k}}$ контрольных точек, которые дают наименьшую ошибку аппроксимации для данного количества кубических сегментов.

Использование четырех кривых

Учитывая только 90-градусный блок-круговой дуга в первый квадрант, мы определяем конечные точки ${ displaystyle mathbf {A}}$ и ${ displaystyle mathbf {B}}$ с контрольными точками ${ displaystyle mathbf {A '}}$ и ${ displaystyle mathbf {B '}}$ соответственно как:

{ displaystyle { begin {align} mathbf {A} & = [0,1] mathbf {A '} & = [ mathbf {k}, 1] mathbf {B'} & = [1, mathbf {k}] mathbf {B} & = [1,0] конец {выровнено}}}

Из определения кубической кривой Безье имеем:

{ displaystyle mathbf {C} (t) = (1-t) ^ {3} mathbf {A} +3 (1-t) ^ {2} t mathbf {A '} +3 (1-t ) t ^ {2} mathbf {B '} + t ^ {3} mathbf {B}}

С точкой ${ displaystyle mathbf {C} (t = 0,5)}$ в качестве середины дуги мы можем записать следующие два уравнения:

{ displaystyle { begin {align} mathbf {C} & = { frac {1} {8}} mathbf {A} + { frac {3} {8}} mathbf {A '} + { frac {3} {8}} mathbf {B '} + { frac {1} {8}} mathbf {B} mathbf {C} & = { sqrt {1/2}} = { sqrt {2}} / 2 конец {выровнено}}}

Решение этих уравнений для координаты x (и аналогично для координаты y) дает:

{ displaystyle { frac {0} {8}} mathbf {+} { frac {3} {8}} mathbf {k} + { frac {3} {8}} + { frac {1 } {8}} = { sqrt {2}} / 2}

{ displaystyle mathbf {k} = { frac {4} {3}} ({ sqrt {2}} - 1) приблизительно 0,5522847498}

Общий случай

Мы можем составить круг радиуса ${ displaystyle R}$ из произвольного числа кубических кривых Безье.^[12]Пусть дуга начинается в точке ${ displaystyle mathbf {A}}$ и закончить в точке ${ displaystyle mathbf {B}}$ , размещенный на равных расстояниях выше и ниже оси x, охватывающий дугу угла ${ displaystyle theta = 2 phi}$ :

{ Displaystyle { begin {align} mathbf {A} _ {x} & = R cos ( phi) mathbf {A} _ {y} & = R sin ( phi) mathbf {B} _ {x} & = mathbf {A} _ {x} mathbf {B} _ {y} & = - mathbf {A} _ {y} end {выровнено}}}

Контрольные точки могут быть записаны как:^[13]

{ displaystyle { begin {align} mathbf {A '} _ {x} & = { frac {4R- mathbf {A} _ {x}} {3}} mathbf {A'} _ {y} & = { frac {(R- mathbf {A} _ {x}) (3R- mathbf {A} _ {x})} {3 mathbf {A} _ {y}}} mathbf {B '} _ {x} & = mathbf {A'} _ {x} mathbf {B '} _ {y} & = - mathbf {A'} _ {y} end {выровнено}}}

Примеры

Восьмисегментный квадратичный поливизье (красный), аппроксимирующий круг (черный) с контрольными точками
Четырехсегментный кубический поливизье (красный), аппроксимирующий круг (черный) с контрольными точками

Шрифты

TrueType шрифты используют составной Безье, состоящий из квадратичный Кривые Безье (кривые 2-го порядка). Чтобы описать типичный шрифтовой дизайн как компьютерный шрифт с любой заданной точностью Безье 3-го порядка требует меньше данных, чем Безье 2-го порядка; а это, в свою очередь, требует меньше данных, чем серия прямых линий. Это верно, даже несмотря на то, что для любого одного сегмента прямой линии требуется меньше данных, чем для любого одного сегмента параболы; и этот параболический сегмент, в свою очередь, требует меньше данных, чем любой сегмент кривой 3-го порядка.

Смотрите также

B-шлиц

Рекомендации

^ Евгений В. Шикин; Александр И. Плис (14 июля 1995 г.). Справочник по шлицам для пользователя. CRC Press. С. 96–. ISBN 978-0-8493-9404-1.
^ Microsoft polybezier API
^ Справочник по API Papyrus Beziergon
^ "Лучшая коробка мелков".InfoWorld.1991.
^ Ребаза, Хорхе (24 апреля 2012 г.). Первый курс прикладной математики. Джон Вили и сыновья. ISBN 9781118277157.
^ (Фирма), Wolfram Research (13 сентября 1996 г.). Стандартные дополнительные пакеты Mathematica ® 3.0. Издательство Кембриджского университета. ISBN 9780521585859.
^ Prautzsch, Hartmut; Бем, Вольфганг; Палушны, Марко (6 августа 2002 г.). Безье и методы B-сплайна. Springer Science & Business Media. ISBN 9783540437611.
^ Бартельс, Ричард Х .; Битти, Джон С .; Барский, Брайан А. (1 января 1987 г.). Введение в сплайны для использования в компьютерной графике и геометрическом моделировании. Морган Кауфманн. ISBN 9781558604001.
^ Агостон, Макс К. (6 декабря 2005 г.). Компьютерная графика и геометрическое моделирование: реализация и алгоритмы. Springer Science & Business Media. ISBN 9781846281082.
^ Станислав, Г. Адам. "Рисование круга кривыми Безье". Получено 10 апреля 2010.
^ «Оцифровка дизайна букв». яблоко. Получено 26 июля 2014.
^ Ришкус, Алексас (октябрь 2006 г.). «АППРОКСИМАЦИЯ КУБИЧЕСКОЙ КРИВОЙ Безье круговыми дугами и токовой версией» (PDF). ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ И КОНТРОЛЬ. Каунасский технологический университет, факультет мультимедийной инженерии. 35 (4): 371–378. ISSN 1392–124X.^{[постоянная мертвая ссылка]}
^ ДеВенеза, Ричард. "Рисование круга кривыми Безье" (PDF). Получено 10 апреля 2010.

[ShikinPlis1995-1] Евгений В. Шикин; Александр И. Плис (14 июля 1995 г.). Справочник по шлицам для пользователя. CRC Press. С. 96–. ISBN 978-0-8493-9404-1.

[2] Microsoft polybezier API

[3] Справочник по API Papyrus Beziergon

[4] "Лучшая коробка мелков".InfoWorld.1991.

[5] Ребаза, Хорхе (24 апреля 2012 г.). Первый курс прикладной математики. Джон Вили и сыновья. ISBN 9781118277157.

[6] (Фирма), Wolfram Research (13 сентября 1996 г.). Стандартные дополнительные пакеты Mathematica ® 3.0. Издательство Кембриджского университета. ISBN 9780521585859.

[7] Prautzsch, Hartmut; Бем, Вольфганг; Палушны, Марко (6 августа 2002 г.). Безье и методы B-сплайна. Springer Science & Business Media. ISBN 9783540437611.

[8] Бартельс, Ричард Х .; Битти, Джон С .; Барский, Брайан А. (1 января 1987 г.). Введение в сплайны для использования в компьютерной графике и геометрическом моделировании. Морган Кауфманн. ISBN 9781558604001.

[9] Агостон, Макс К. (6 декабря 2005 г.). Компьютерная графика и геометрическое моделирование: реализация и алгоритмы. Springer Science & Business Media. ISBN 9781846281082.

[10] Станислав, Г. Адам. "Рисование круга кривыми Безье". Получено 10 апреля 2010.

[11] «Оцифровка дизайна букв». яблоко. Получено 26 июля 2014.

[12] Ришкус, Алексас (октябрь 2006 г.). «АППРОКСИМАЦИЯ КУБИЧЕСКОЙ КРИВОЙ Безье круговыми дугами и токовой версией» (PDF). ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ И КОНТРОЛЬ. Каунасский технологический университет, факультет мультимедийной инженерии. 35 (4): 371–378. ISSN 1392–124X.^{[постоянная мертвая ссылка]}

[13] ДеВенеза, Ричард. "Рисование круга кривыми Безье" (PDF). Получено 10 апреля 2010.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

Navigation