WikiDer > Кривая Безье

А Кривая Безье (/ˈбɛz.я.eɪ/ BEH-зи-ай)[1] это параметрическая кривая используется в компьютерная графика и связанные области.[2] Кривая, относящаяся к Полином Бернштейна, назван в честь Пьер Безье, который использовал его в 1960-х годах для разработки кривых кузова Renault легковые автомобили.[3] Другие варианты использования включают дизайн компьютера шрифты и анимация.[3] Кривые Безье можно объединить, чтобы образовать Сплайн Безье, или обобщить на более высокие измерения, чтобы сформировать Поверхности Безье.[3] В Треугольник Безье является частным случаем последнего.
В векторная графика, Кривые Безье используются для моделирования гладких кривых, которые можно масштабировать до бесконечности. "Пути", как их обычно называют в программах обработки изображений,[примечание 1] представляют собой комбинации связанных кривых Безье. Пути не ограничены пределами растеризованный изображения и интуитивно понятны для изменения.
Кривые Безье также используются во временной области, особенно в анимация, пользовательский интерфейс[заметка 2] проектирование и сглаживание траектории курсора в интерфейсах, управляемых взглядом.[4] Например, кривую Безье можно использовать для определения скорости движения объекта, такого как значок, с течением времени из точки A в точку B, вместо того, чтобы просто перемещаться с фиксированным числом пикселей за шаг. Когда аниматоры или интерфейс дизайнеры говорят о «физике» или «ощущении» операции, они могут иметь в виду конкретную кривую Безье, используемую для управления скоростью во времени рассматриваемого движения.
Это также относится к робототехнике, где, например, движение сварочного рычага должно быть плавным, чтобы избежать ненужного износа.
Изобретение
Математическая основа кривых Безье - Многочлены Бернштейна- была создана в 1912 году, но полиномы не применялись в графике до 50 лет спустя, когда математик Поль де Кастельжау в 1959 г. алгоритм де Кастельжау, а численно стабильный метод оценки кривых, и стал первым, кто применил их для автоматизированного проектирования на французском автопроизводителе. Citroën.[5] Многочлены были широко известны в 1960-х годах. Французский инженер Пьер Безье, кто использовал их для дизайна автомобиль тела в Renault.
Конкретные случаи
Кривая Безье определяется набором контрольные точки п0 через пп, куда п называется его порядком (п = 1 для линейного, 2 для квадратичного и т. Д.). Первая и последняя контрольные точки всегда являются конечными точками кривой; однако промежуточные контрольные точки (если они есть) обычно не лежат на кривой. Суммы в следующих разделах следует понимать как аффинные комбинации, сумма коэффициентов равна 1.
Линейные кривые Безье
Учитывая разные точки п0 и п1, линейная кривая Безье - это просто прямая линия между этими двумя точками. Кривая задается
и эквивалентен линейная интерполяция.
Квадратичные кривые Безье

Квадратичная кривая Безье - это путь, пройденный функцией B(т), учитывая баллы п0, п1, и п2,
- ,
который можно интерпретировать как линейный интерполянт соответствующих точек на линейных кривых Безье из п0 к п1 и из п1 к п2 соответственно. Преобразование предыдущего уравнения дает:
Это можно записать таким образом, чтобы подчеркнуть симметрию относительно п1:
Что сразу дает производную кривой Безье по т:
из чего можно сделать вывод, что касательные к кривой при п0 и п2 пересекаться в п1. В качестве т возрастает от 0 до 1, кривая отходит от п0 в направлении п1, затем изгибается, чтобы достичь п2 со стороны п1.
Вторая производная кривой Безье по т является
Кубические кривые Безье
Четыре балла п0, п1, п2 и п3 на плоскости или в многомерном пространстве определяют кубическую кривую Безье. Кривая начинается в п0 идущий к п1 и прибывает в п3 идущий со стороны п2. Обычно он не проходит п1 или же п2; эти точки служат только для получения информации о направлении. Расстояние между п1 и п2 определяет «как далеко» и «насколько быстро» кривая движется в сторону п1 прежде чем повернуться к п2.
Письмо Bпя,пj,пk(т) квадратичной кривой Безье, определяемой точками пя, пj, и пkкубическая кривая Безье может быть определена как аффинная комбинация двух квадратичных кривых Безье:
Явный вид кривой:
Для некоторых вариантов п1 и п2 кривая может пересекаться сама с собой или содержать куспид.
Любую серию из 4 различных точек можно преобразовать в кубическую кривую Безье, которая проходит через все 4 точки по порядку. Задав начальную и конечную точки некоторой кубической кривой Безье, а также точки вдоль кривой, соответствующие т = 1/3 и т = 2/3, можно восстановить контрольные точки исходной кривой Безье.[6]
Производная кубической кривой Безье по т является
Вторая производная кривой Безье по т является
Общее определение
Кривые Безье могут быть определены для любой степени п.
Рекурсивное определение
Рекурсивное определение кривой Безье степени п выражает это как точка-точка линейная комбинация (линейная интерполяция) пары соответствующих точек двух кривых Безье степени п − 1.
Позволять обозначают кривую Безье, определяемую любым выбором точек п0, п1, ..., пп. Затем, чтобы начать,
Эта рекурсия поясняется в анимации ниже.
Явное определение
Формула может быть выражена явно следующим образом:
куда являются биномиальные коэффициенты.
Например, для п = 5:
Терминология
С этими параметрическими кривыми связана некоторая терминология. У нас есть
где многочлены
известны как Базисные полиномы Бернштейна степени п.
Обратите внимание, что т0 = 1, (1 − т)0 = 1, и что биномиальный коэффициент, , является:
Точки пя называются контрольные точки для кривой Безье. В многоугольник образованный соединением точек Безье с линии, начиная с п0 и заканчивая пп, называется Многоугольник Безье (или же контрольный многоугольник). В выпуклый корпус многоугольника Безье содержит кривую Безье.
Полиномиальная форма
Иногда желательно выразить кривую Безье в виде многочлен вместо суммы менее простых Многочлены Бернштейна. Применение биномиальная теорема к определению кривой с последующей некоторой перестановкой даст:
куда
Это может быть практично, если могут быть вычислены до многих оценок ; однако следует проявлять осторожность, поскольку кривые высокого порядка могут не иметь числовая стабильность (алгоритм де Кастельжау следует использовать, если это произойдет). Обратите внимание, что пустой продукт равно 1.
Характеристики
- Кривая начинается в п0 и заканчивается в пп; это так называемый конечная интерполяция свойство.
- Кривая является прямой, если и только если все контрольные точки коллинеарен.
- Начало и конец кривой касательная к первому и последнему участку многоугольника Безье соответственно.
- Кривая может быть разделена в любой точке на две подкривые или на произвольное количество подкривых, каждая из которых также является кривой Безье.
- Некоторые кривые, которые кажутся простыми, например круг, не может быть точно описан Безье или кусочно Кривая Безье; хотя кубическая кривая Безье из четырех частей может аппроксимировать круг (см. составная кривая Безье) с максимальной радиальной погрешностью менее одной части из тысячи, когда каждая внутренняя контрольная точка (или автономная точка) представляет собой расстояние горизонтально или вертикально от внешней контрольной точки на единичной окружности. В более общем плане пкубическая кривая Безье может приближаться к окружности, когда каждая внутренняя контрольная точка - это расстояние из внешней контрольной точки на единичной окружности, где т составляет 360 /п градусы и п > 2.
- Каждая квадратичная кривая Безье также является кубической кривой Безье и, в более общем смысле, каждая степень п Кривая Безье - это тоже степень м кривая для любого м > п. В частности, степень п кривая с контрольными точками п0, ..., пп эквивалентно (включая параметризацию) степени п + 1 кривая с контрольными точками П'0, ..., П'п + 1, куда .
- Кривые Безье имеют свойство уменьшения вариации. Интуитивно это означает, что кривая Безье не «волнообразна» больше, чем многоугольник ее контрольных точек, и на самом деле может «волнообразно» меньше.[7]
- Здесь нет местное управление в степени п Кривые Безье - это означает, что любое изменение контрольной точки требует перерасчета и, таким образом, влияет на аспект всей кривой, «хотя чем дальше от контрольной точки, которая была изменена, тем меньше изменение кривой».[8]
- Кривая Безье более высокого порядка, чем два, может пересекаться сама с собой или иметь острие для определенного выбора контрольных точек.
Кривая второго порядка - параболический отрезок
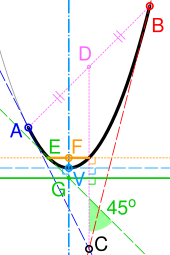
Квадратичная кривая Безье также является отрезком кривой парабола. Поскольку парабола - это коническая секция, некоторые источники называют квадратичные Безье «коническими дугами».[9] Со ссылкой на рисунок справа, важные характеристики параболы могут быть получены следующим образом:[10]
- Касательные к параболе в конечных точках кривой (A и B) пересекаются в ее контрольной точке (C).
- Если D - середина AB, касательная к кривой, перпендикулярной CD (пунктирная голубая линия), определяет ее вершину (V). Его ось симметрии (голубой штрих-пунктир) проходит через V и перпендикулярна касательной.
- E - любая точка на кривой с касательной под углом 45 ° к CD (пунктирная зеленая линия). Если G является пересечением этой касательной и оси, прямая, проходящая через G и перпендикулярная CD, является директрисой (сплошной зеленый цвет).
- Фокус (F) находится на пересечении оси и линии, проходящей через E и перпендикулярной CD (желтая пунктирная линия). Прямая кишка - это линейный сегмент внутри кривой (сплошной желтый).
Производная
Производная для кривой порядка п является
Построение кривых Безье
Линейные кривые
В т в функции для линейной кривой Безье можно рассматривать как описание того, насколько далеко B(т) из п0 к п1. Например, когда t = 0,25, B(т) находится в четверти пути от точки п0 к п1. В качестве т варьируется от 0 до 1, B(т) описывает прямую из п0 к п1.
![Анимация линейной кривой Безье, t в [0,1]](http://upload.wikimedia.org/wikipedia/commons/thumb/0/00/B%C3%A9zier_1_big.gif/240px-B%C3%A9zier_1_big.gif) |
| Анимация линейной кривой Безье, т в [0,1] |
Квадратичные кривые
Для квадратичных кривых Безье можно построить промежуточные точки Q0 и Q1 так что как т варьируется от 0 до 1:
- Точка Q0(т) варьируется от п0 к п1 и описывает линейную кривую Безье.
- Точка Q1(т) варьируется от п1 к п2 и описывает линейную кривую Безье.
- Точка B(т) линейно интерполируется между Q0(т) к Q1(т) и описывает квадратичную кривую Безье.
 | ![Анимация квадратичной кривой Безье, t в [0,1]](http://upload.wikimedia.org/wikipedia/commons/thumb/3/3d/B%C3%A9zier_2_big.gif/240px-B%C3%A9zier_2_big.gif) | |
| Построение квадратичной кривой Безье | Анимация квадратичной кривой Безье, т в [0,1] |
Кривые высшего порядка
Соответственно, для кривых более высокого порядка требуется больше промежуточных точек. Для кубических кривых можно построить промежуточные точки Q0, Q1, и Q2 описывающие линейные кривые Безье и точки р0 & р1 описывающие квадратичные кривые Безье:
 | ![Анимация кубической кривой Безье, t в [0,1]](http://upload.wikimedia.org/wikipedia/commons/thumb/d/db/B%C3%A9zier_3_big.gif/240px-B%C3%A9zier_3_big.gif) | |
| Построение кубической кривой Безье | Анимация кубической кривой Безье, т в [0,1] |
Для кривых четвертого порядка можно построить промежуточные точки Q0, Q1, Q2 & Q3 описывающие линейные кривые Безье, точки р0, р1 & р2 описывающие квадратичные кривые Безье, и точки S0 & S1 которые описывают кубические кривые Безье:
 | ![Анимация кривой Безье четвертой степени, t в [0,1]](http://upload.wikimedia.org/wikipedia/commons/thumb/a/a4/B%C3%A9zier_4_big.gif/240px-B%C3%A9zier_4_big.gif) | |
| Построение кривой Безье четвертой степени | Анимация кривой Безье четвертой степени, т в [0,1] |
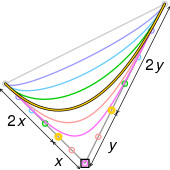
Для кривых пятого порядка можно построить аналогичные промежуточные точки.
 |
| Анимация кривой Безье пятого порядка, т в [0,1] красным. Также показаны кривые Безье для каждого из нижних порядков. |
Эти представления основаны на процессе, используемом в Алгоритм де Кастельжау для расчета кривых Безье.[11]
Смещения (также известные как обводка) кривых Безье
Кривая с фиксированным смещением от заданной кривой Безье, называемая смещение или параллельная кривая по математике (лежать «параллельно» исходной кривой, как смещение между рельсами в железнодорожные пути), не может быть точно образована кривой Безье (за исключением некоторых тривиальных случаев). В общем, двусторонняя кривая смещения кубической кривой Безье - это 10-й порядок алгебраическая кривая[12] и вообще для степени Безье п кривая двустороннего смещения представляет собой алгебраическую кривую степени 4п-2.[13] Однако есть эвристический методы, которые обычно дают адекватное приближение для практических целей.[14]
В области векторная графика, рисование двух симметрично расположенных кривых смещения называется поглаживание (кривая Безье или вообще путь из нескольких отрезков Безье).[12] Преобразование из кривых смещения в контуры Безье с заливкой имеет практическое значение при преобразовании шрифты определено в Метафонт, позволяющий обводить кривые Безье до более широко используемых Шрифты PostScript типа 1, которые позволяют (в целях повышения эффективности) только математически более простую операцию заполнения контура, определенного (несамопересекающимися) кривыми Безье.[15]
Степень возвышения
Кривая Безье степени п можно преобразовать в кривую Безье степени п + 1 с такой же формой. Это полезно, если программное обеспечение поддерживает кривые Безье только определенной степени. Например, системы, которые могут работать только с кубическими кривыми Безье, могут неявно работать с квадратичными кривыми, используя их эквивалентное кубическое представление.
Для повышения степени мы используем равенство Каждый компонент умножается на (1 -т) ит, таким образом увеличивая градус на единицу без изменения значения. Вот пример увеличения степени от 2 до 3.
Для произвольных п мы используем равенства
Следовательно:
введение произвольных и .
Следовательно, новые контрольные точки [16]
Повторное повышение градуса
Концепция градусного повышения может быть повторена на контрольном многоугольнике. р получить последовательность управляющих полигонов р,р1,р2, и так далее. После р градус высот, многоугольник рр имеет вершины п0, г,п1, г,п2, г,...,пп + г, г данный [16]
Также можно показать, что для базовой кривой Безье B,
Рациональные кривые Безье
Рациональная кривая Безье добавляет регулируемые веса, чтобы обеспечить более точное приближение к произвольным формам. Числитель - это взвешенная кривая Безье в форме Бернштейна, а знаменатель - взвешенная сумма Многочлены Бернштейна. Рациональные кривые Безье могут, среди прочего, использоваться для представления сегментов конические секции ровно, включая дуги окружности.[17]
Данный п + 1 контрольная точка пя, рациональную кривую Безье можно описать следующим образом:
или просто
Выражение может быть расширено за счет использования числовых систем помимо действительных чисел для весов. На комплексной плоскости точки {1}, {-1} и {1} с весами { }, {1} и {} создать полный круг с радиусом один. Для кривых с точками и весами на окружности веса можно масштабировать без изменения формы кривой. [18] Масштабирование центрального веса приведенной выше кривой на 1,35508 дает более однородную параметризацию.
Приложения
Компьютерная графика

Кривые Безье широко используются в компьютерной графике для моделирования плавных кривых. Поскольку кривая полностью содержится в выпуклый корпус своего контрольные точки, точки могут отображаться графически и использоваться для интуитивного управления кривой. Аффинные преобразования Такие как перевод и вращение можно применить к кривой, применив соответствующее преобразование к контрольным точкам кривой.
Квадратичный и кубический Кривые Безье наиболее распространены. Кривые более высокой степени больше вычислительно дорогой оценить. Когда требуются более сложные формы, кривые Безье низкого порядка соединяются вместе, образуя составная кривая Безье. Составная кривая Безье обычно называется «траекторией» в векторная графика языки (например, PostScript), стандарты векторной графики (например, SVG) и программы векторной графики (например, Artline, Издатель Timeworks, Adobe Illustrator, CorelDraw, Inkscape, и Аллегро). Чтобы объединить кривые Безье в составную кривую Безье без перегибов, необходимо свойство, называемое G1 непрерывный, достаточно заставить контрольную точку, в которой встречаются две составляющие кривые Безье, лежать на линии, определяемой двумя контрольными точками с каждой стороны.

Самый простой способ преобразования скана (растеризация) кривая Безье состоит в том, чтобы оценить ее во многих близко расположенных точках и преобразовать сканирование в аппроксимирующую последовательность отрезков линии. Однако это не гарантирует, что растеризованный результат будет выглядеть достаточно гладким, поскольку точки могут быть расположены слишком далеко друг от друга. И наоборот, это может создать слишком много точек в областях, где кривая близка к линейной. Распространенным адаптивным методом является рекурсивное подразделение, при котором контрольные точки кривой проверяются, чтобы увидеть, приближается ли кривая к прямой с небольшим допуском. Если нет, кривая параметрически разделяется на два сегмента, 0 ≤ т ≤ 0,5 и 0,5 ≤ т ≤ 1, и та же процедура применяется рекурсивно к каждой половине. Существуют также методы прямого дифференцирования, но при анализе распространения ошибок необходимо проявлять особую осторожность.[20]
Аналитические методы, при которых линия Безье пересекается с каждой линией сканирования, включают поиск корней кубических многочленов (для кубических Безье) и работу с несколькими корнями, поэтому они не часто используются на практике.[20]
Алгоритм растеризации, используемый в Метафонт основан на дискретизации кривой, чтобы она была аппроксимирована последовательностью "ладья перемещается ", которые являются чисто вертикальными или чисто горизонтальными, вдоль границ пикселей. Для этого плоскость сначала разбивается на восемь секторов под углом 45 ° (осями координат и двумя линиями ), то кривая разбивается на более мелкие отрезки, так что направление сегмента кривой остается в пределах одного сектора; так как скорость кривой является полиномом второй степени, нахождение значения, когда она параллельна одной из этих линий, могут быть получены путем решения квадратных уравнений. Внутри каждого сегмента преобладает горизонтальное или вертикальное движение, и общее количество шагов в любом направлении можно считать по координатам конечной точки; например, в этом случае преобладает горизонтальное движение вправо в секторе 0–45 °, поэтому остается только решить, между какими шагами вправо кривая должна сделать шаг вверх.[21]
Анимация
В анимационных приложениях, таких как Adobe Flash и Synfig, Кривые Безье используются для обозначения, например, движения. Пользователи намечают желаемый путь в кривых Безье, и приложение создает необходимые рамки для перемещения объекта по контуру.[22][23]
В трехмерной анимации кривые Безье часто используются для определения трехмерных путей, а также двумерных кривых для интерполяции ключевых кадров.[24] Кривые Безье теперь очень часто используются для управления замедлением анимации в CSS, JavaScript и JavaFx.
Шрифты
TrueType шрифты используют составные кривые Безье, состоящие из квадратичный Кривые Безье. Другие языки и инструменты обработки изображений (например, PostScript, Асимптота, Метафонт, и SVG) использовать составной Безье, состоящий из кубический Кривые Безье для рисования изогнутых форм. OpenType шрифты могут использовать любой вид, в зависимости от разновидности шрифта.[25]
Внутренний рендеринг всех кривых Безье в средствах рендеринга шрифтов или векторной графики будет рекурсивно разделить их до точки, в которой кривая будет достаточно плоской, чтобы ее можно было нарисовать как серию линейных или круговых сегментов. Точный алгоритм разделения зависит от реализации, должны соблюдаться только критерии плоскостности, чтобы достичь необходимой точности и избежать немонотонных локальных изменений кривизны. Функция «плавной кривой» графиков в Майкрософт Эксель также использует этот алгоритм.[26]
Поскольку дуги окружностей и эллипсов не могут быть точно представлены кривыми Безье, они сначала аппроксимируются кривыми Безье, которые, в свою очередь, аппроксимируются дугами окружностей. Это неэффективно, поскольку существуют также аппроксимации всех кривых Безье с использованием дуг окружностей или эллипсов, которые могут отображаться постепенно с произвольной точностью. Другой подход, используемый современными аппаратными графическими адаптерами с ускоренной геометрией, может преобразовывать точно все кривые Безье и конические кривые (или поверхности) в NURBS, который можно визуализировать постепенно, без предварительного рекурсивного разделения кривой для достижения необходимого условия плоскостности. Этот подход также позволяет сохранить определение кривой при всех линейных или перспективных 2D и 3D преобразованиях и проекциях.[нужна цитата]
Двигатели шрифтов, например FreeType, нарисуйте кривые (и линии) шрифта на пиксельной поверхности, используя процесс, известный как растеризация шрифтов.[9]
Смотрите также
- Безье поверхность
- B-шлиц
- GEM / 4 & GEM / 5
- Кривая Эрмита
- NURBS
- Струнное искусство - Кривые Безье также образованы многими распространенными формами струнного искусства, где струны наматываются на гвоздь.[27]
- Свойство уменьшения вариации кривых Безье
Примечания
- ^ Программы обработки изображений, такие как Inkscape, Adobe Photoshop, и GIMP.
- ^ В анимационных приложениях, таких как Adobe Flash, Adobe After Effects, Смесь Microsoft Expression, Блендер, Autodesk Maya и Autodesk 3ds max.
Рекомендации
Цитаты
- ^ Уэллс, Джон (3 апреля 2008 г.). Словарь произношения Longman (3-е изд.). Пирсон Лонгман. ISBN 978-1-4058-8118-0.
- ^ Мортенсон, Майкл Э. (1999). Математика для приложений компьютерной графики. Industrial Press Inc. стр. 264. ISBN 9780831131111.
- ^ а б c Hazewinkel, Michiel (1997). Энциклопедия математики: Приложение. 1. Springer Science & Business Media. п. 119. ISBN 9780792347095.
- ^ Бисвас, Прадипта; Лэнгдон, Пэт (2015-04-03). «Мультимодальная интеллектуальная система отслеживания взгляда». Международный журнал взаимодействия человека и компьютера. 31 (4): 277–294. Дои:10.1080/10447318.2014.1001301. ISSN 1044-7318. S2CID 36347027.
- ^ Джеральд Э. Фарин; Йозеф Хошек; Мён Су Ким (2002). Справочник по компьютерному геометрическому дизайну. Эльзевир. С. 4–6. ISBN 978-0-444-51104-1.
- ^ Джон Буркардт. "Принуждение к интерполяции Безье". Архивировано из оригинал на 2013-12-25.
- ^ Теофило Гонсалес; Хорхе Диас-Эррера; Аллен Такер (2014). Справочник по вычислениям, третье издание: компьютерные науки и программная инженерия. CRC Press. стр. 32-14. ISBN 978-1-4398-9852-9.
- ^ Макс К. Агостон (2005). Компьютерная графика и геометрическое моделирование: реализация и алгоритмы. Springer Science & Business Media. п. 404. ISBN 978-1-84628-108-2.
- ^ а б «Условные обозначения FreeType для глифов / VI. Основные положения FreeType». Проект свободного типа. 13 февраля 2018.
«Соглашения о символах FreeType - Версия 2.1 / VI. Общие сведения о FreeType». 6 марта 2011. Архивировано с оригинал 29 сентября 2011 г. - ^ Дункан Марш (2005). Прикладная геометрия для компьютерной графики и САПР. Серия «Математика бакалавриата Springer» (2-е изд.). ISBN 978-1-85233-801-5. КАК В 1852338016.
- ^ Шене, К.К. «Нахождение точки на кривой Безье: алгоритм де Кастельжау». Получено 6 сентября 2012.
- ^ а б Марк Килгард (10 апреля 2012 г.). "CS 354 Векторная графика и рендеринг контуров". п. 28.
- ^ Рида Т. Фаруки. «Введение в кривые Пифагора-годографа» (PDF)., в частности стр. 16 «Таксономия офсетных кривых».
- ^ Например: [1] или же [2]. Для обзора см. [3].
- ^ Ричард Дж. Кинч (1995). «MetaFog: преобразование форм Metafont в контуры» (PDF). ТУГбоат. 16 (3 – Материалы годового собрания 1995 г.).
- ^ а б Фарин, Джеральд (1997). Кривые и поверхности для компьютерного геометрического проектирования (4-е изд.). Эльзевир Книги по науке и технологиям. ISBN 978-0-12-249054-5.
- ^ Нил Доджсон (2000-09-25). «Некоторые математические элементы графики: рациональные B-сплайны». Получено 2009-02-23.
- ^ Х. Санчес-Рейес (ноябрь 2009 г.). «Комплексные рациональные кривые Безье». Компьютерный геометрический дизайн. 26 (8): 865–876. Дои:10.1016 / j.cagd.2009.06.003.
- ^ Александр Решетов и Дэвид Любке, Intersector Phantom Ray-Hair. В материалах ACM по компьютерной графике и интерактивным методам (1 августа 2018 г.). [4]
- ^ а б Сюэсян Ли и Цзюньсяо Сюэ. «Комплексная квадратичная кривая Безье на единичной окружности». Чжэнчжоу, Китай: Школа программного обеспечения Университета Чжэнчжоу.
- ^ Части 19–22 Кнут, Дональд Э. (1986). Метафонт: Программа. Эддисон-Уэсли. ISBN 0-201-13438-1.
- ^ «Использование траекторий движения в анимации». Adobe. Получено 2019-04-11.
- ^ "Следование по сплайну". Synfig Вики. Получено 2019-04-11.
- ^ Доджсон, Нил А. (1999). «Конспект лекций по продвинутой графике» (PDF). cl.cam.ac.uk. Компьютерная лаборатория Кембриджского университета.
- ^ «Разница между CFF и TTF». Секрет производства. Линотип. Архивировано из оригинал на 2017-07-03. Получено 3 июля 2018.
Формат OpenType был сформулирован в 1996 году. К 2003 году он начал заменять два конкурирующих формата: шрифты Type1, разработанные Adobe и основанные на скрипте [P] ost [S], и шрифты TrueType, определенные Microsoft и Apple. (...) TTF означает TrueTypeFont и указывает, что данные шрифта такие же, как и в шрифтах TrueType. CFF означает формат шрифта Type1. Строго говоря, это относится к компактному формату шрифтов, который используется в процессах сжатия для шрифтов Type2. (...) кубический формат Безье шрифтов Type1 более экономит место по сравнению с квадратичным форматом шрифтов TrueType. Некоторые килобайты можно сэкономить в больших сложных шрифтах, что может дать преимущество в Интернете. С другой стороны, более подробная информация о подсказках шрифтов TrueType позволяет значительно оптимизировать использование экрана.
- ^ "smooth_curve_bezier_example_file.xls". Rotating Machinery Analysis, Inc. Архивировано из оригинал на 2011-07-18. Получено 2011-02-05.
- ^ Гросс, Р. (2014). «Мосты, струнное искусство и кривые Безье». В Питичи, Мирча (ред.). Лучшая работа по математике 2013 г.. Лучшая работа по математике 2013 г.. Пенроуз Р. (Автор) и Питичи М. (Ред.). Издательство Принстонского университета. С. 77–89. Дои:10.1515/9781400847990-011. ISBN 9780691160412. JSTOR j.ctt4cgb74.13.
Источники
- Рида Т. Фаруки (август 2012 г.). "Основание полиномов Бернштейна: столетняя ретроспектива" (PDF). Компьютерный геометрический дизайн. 29 (6): 379–419. Дои:10.1016 / j.cagd.2012.03.001.
- Пол Бурк (19 июля 2009 г.). Поверхности Безье (в 3D). Архивировано из оригинал 19 июля 2009 г.
- Дональд Кнут (1986). Метафонт: Программа. Эддисон-Уэсли. С. 123–131. Отличное обсуждение деталей реализации; доступен бесплатно как часть дистрибутива TeX.
- Томас Седерберг. Кривые Безье (PDF). Архивировано из оригинал (PDF) 21 февраля 2006 г.. Получено 2005-09-14.
- Дж. Д. Фоли; и другие. (1992). Компьютерная графика: принципы и практика на C (2-е изд.). Эддисон Уэсли.
- Раджив Чандель (2014-03-20). «Применение кривых Безье в играх».
дальнейшее чтение
- Учебник по кривым Безье—Онлайн-книга с открытым исходным кодом, объясняющая кривые Безье и связанные с ними графические алгоритмы с интерактивной графикой.
- Кубические кривые Безье - Под капотом (видео) Видео показывает, как компьютеры визуализируют кубическую кривую Безье, автор Питер Новелл.
- От Безье до Бернштейна Столбец функций из Американское математическое общество
- «Кривая Безье», Энциклопедия математики, EMS Press, 2001 [1994]
- Prautzsch, Hartmut; Бем, Вольфганг; Палушны, Марко (2002). Безье и методы B-сплайна. Springer Science & Business Media. ISBN 978-3-540-43761-1.
- Галье, Жан (1999). "Глава 5. Полиномиальные кривые как кривые Безье". Кривые и поверхности в геометрическом моделировании: теория и алгоритмы. Морган Кауфманн. Эта книга больше не издается и находится в свободном доступе у автора.
- Фарин, Джеральд Э. (2002). Кривые и поверхности для CAGD: Практическое руководство (5-е изд.). Морган Кауфманн. ISBN 978-1-55860-737-8.
- Вайсштейн, Эрик В. «Кривая Безье». MathWorld.
- Гофман, Гернот. "Кривые Безье" (PDF). Архивировано из оригинал (PDF) на 2006-12-02. (60 страниц)
- Ан, Ён Джун (2004). «Аппроксимация дуг окружности и кривых смещения кривыми Безье высокой степени». Журнал вычислительной и прикладной математики. 167 (2): 405–416. Bibcode:2004JCoAM.167..405A. Дои:10.1016 / j.cam.2003.10.008.
- Дэвис, Джейсон. «Анимированные кривые Безье».
внешняя ссылка
- Компьютерный код


![mathbf {B} (t) = (1-t) [(1-t) mathbf {P} _ {0} + tmathbf {P} _ {1}] + t [(1-t) mathbf {P} _ {1} + tmathbf {P} _ {2}] {mbox {,}} 0leq tleq 1](https://wikimedia.org/api/rest_v1/media/math/render/svg/d198fcc2309af8ef4d56a45b3b4a9eefde048635)