WikiDer > Граф Дюрера
в математический поле теория графов, то Граф Дюрера является неориентированный граф с 12 вершинами и 18 ребрами. Он назван в честь Альбрехт Дюрер, чья 1514 гравировка Меленколия I включает изображение Твердое тело Дюрера, а выпуклый многогранник имея граф Дюрера в качестве скелет. Твердость Дюрера - одна из четырех хорошо покрытый просто выпуклые многогранники.
Твердое тело Дюрера
Тело Дюрера комбинаторно эквивалентно телу куб с двумя противоположными вершинами усеченный,[1] хотя Дюрер описывает его не в этой форме, а как усеченный ромбоэдр или треугольный усеченный трапецоэдр.[2] Точная геометрия твердого тела, изображенного Дюрером, является предметом некоторых академических дебатов с различными гипотетическими значениями для его острых углов в диапазоне от 72 ° до 82 °.[3]
Теоретико-графические свойства
| Граф Дюрера | |
|---|---|
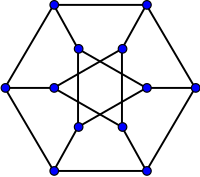 Граф Дюрера | |
| Названный в честь | Альбрехт Дюрер |
| Вершины | 12 |
| Края | 18 |
| Радиус | 3 |
| Диаметр | 4 |
| Обхват | 3 |
| Автоморфизмы | 12 (D6) |
| Хроматическое число | 3 |
| Хроматический индекс | 3 |
| Свойства | Кубический Планарный хорошо покрытый |
| Таблица графиков и параметров | |
Граф Дюрера - это граф, образованный вершинами и ребрами тела Дюрера. Это кубический граф из обхват 3 и диаметр 4. Так же как его конструкция, как каркас тела Дюрера, его можно получить, применяя Y-Δ преобразование в противоположные вершины куб граф, или как обобщенный граф Петерсена г(6,2). Как и любой график выпуклого многогранника, граф Дюрера является 3-вершинно-связанный просто планарный граф.
Граф Дюрера - это хорошо покрытый граф, что означает, что все его максимальные независимые множества имеют одинаковое количество вершин, четыре. Это один из четырех хорошо покрытых кубических многогранных графов и один из семи хорошо покрытых 3-связных кубических графов. Только остальные три хорошо прикрыты просто выпуклые многогранники тетраэдр, треугольная призма, и пятиугольная призма.[4]
Граф Дюрера есть Гамильтониан, с участием Обозначение LCF [-4,5,2,-4,-2,5;-].[5] Точнее, он имеет ровно шесть гамильтоновых циклов, каждая пара из которых может отображаться друг в друга с помощью симметрии графа.[6]
Симметрии
В группа автоморфизмов как граф Дюрера, так и твердое тело Дюрера (либо в форме усеченного куба, либо в форме, показанной Дюрером) изоморфны группа диэдра порядка 12: D6.
Галерея
Хроматический индекс графа Дюрера равен 3.
Хроматическое число графа Дюрера равно 3.
Граф Дюрера есть Гамильтониан.
 | Викискладе есть медиафайлы по теме Граф Дюрера. |
Примечания
- ^ Вайсштейн, Эрик В. «Твердое тело Дюрера». MathWorld.
- ^ Вебер (1900).
- ^ Вайцель (2004).
- ^ Кэмпбелл и Пламмер (1988); Кэмпбелл, Эллингем и Ройл (1993).
- ^ Кастанья и Принс (1972) приписывают доказательство гамильтоничности класса обобщенных графов Петерсена, который включает граф Дюрера, докторской диссертации 1968 г. диссертация Г. Н. Робертсона в Университете Ватерлоо.
- ^ Швенк (1989).
Рекомендации
- Кэмпбелл, S. R .; Эллингем, М.Н.; Ройл, Гордон Ф. (1993), "Характеристика хорошо покрытых кубических графов", Журнал комбинаторной математики и комбинаторных вычислений, 13: 193–212, Г-Н 1220613.
- Кэмпбелл, Стивен Р .; Пламмер, Майкл Д. (1988), "О хорошо покрытых 3-многогранниках", Ars Combinatoria, 25 (А): 215–242, Г-Н 0942505.
- Кастанья, Франк; Принс, Герт (1972), "Каждый обобщенный граф Петерсена имеет окраску тайта", Тихоокеанский математический журнал, 40: 53–58, Дои:10.2140 / pjm.1972.40.53.
- Швенк, Аллен Дж. (1989), "Перечисление гамильтоновых циклов в некоторых обобщенных графах Петерсена", Журнал комбинаторной теории, Серия B, 47 (1): 53–59, Дои:10.1016/0095-8956(89)90064-6, Г-Н 1007713.
- Вебер, П. (1900), Beiträge zu Dürers Weltanschauung — Eine Studie über die drei Stiche Ritter, Tod und Teufel, Melancholie und Hieronymus im Gehäus, Страсбург. Как цитирует Вайцель (2004).
- Weitzel, Hans (2004), "Еще одна гипотеза о многограннике на гравюре А. Дюрера Melencolia I", Historia Mathematica, 31 (1): 11–14, Дои:10.1016 / S0315-0860 (03) 00029-6.