WikiDer > Электронная плотность
В квантовая химия электронная плотность или же электронная плотность это мера вероятность из электрон присутствовать в бесконечно малом элементе пространства, окружающем любую данную точку. Это скалярная величина, зависящая от трех пространственных переменных, и обычно обозначается как или же . Плотность определяется путем определения нормированным -электрон волновая функция который сам зависит от переменные ( пространственные и вращение координаты). И наоборот, плотность определяет волновую функцию по модулю с точностью до фазового множителя, обеспечивая формальную основу для теория функционала плотности.
В соответствии с квантовая механика, из-за принцип неопределенности в атомном масштабе невозможно предсказать точное местоположение электрона, только вероятность его нахождения в данном положении; поэтому электроны в атомах и молекулах действуют так, как будто они «размазаны» в пространстве. Для одноэлектронных систем концентрация электронов в любой точке пропорциональна квадрату величины волновая функция.
Определение
Электронная плотность, соответствующая нормированной -электрон волновая функция (с и обозначающие пространственные и спиновые переменные соответственно) определяется как[1]
где оператор, соответствующий наблюдаемой плотности, есть
Вычисление как определено выше, мы можем упростить выражение следующим образом.
Проще говоря: удерживая единственный электрон на месте мы суммируем все возможные варианты расположения других электронов.
В Хартри – Фок и функционал плотности теории волновую функцию обычно представляют как Определитель Слейтера построен из орбитали , с соответствующими профессиями . В этих ситуациях плотность упрощается до
Общие свойства
По определению, электронная плотность - это неотрицательная функция, интегрируемая с общим числом электронов. Далее, для системы с кинетической энергией Т, плотность удовлетворяет неравенствам[2]
Для конечных кинетических энергий первое (более сильное) неравенство помещает квадратный корень из плотности в Соболевское пространство . Вместе с нормализацией и неотрицательностью это определяет пространство, содержащее физически приемлемые плотности, как
Второе неравенство помещает плотность в L3 Космос. Вместе со свойством нормализации допускает допустимую плотность в пределах пересечения L1 и L3 - расширенный набор .
Топология
В основное состояние электронная плотность атом предполагается, что это монотонно убывающая функция расстояния от ядро.[3]
Состояние ядерного острия
Электронная плотность показывает каспы на каждом ядре в молекуле в результате неограниченного электрон-ядерного кулоновского потенциала. Это поведение количественно выражается условием возврата Като, сформулированным в терминах сферически усредненной плотности, , о любом заданном ядре как[4]
То есть, радиальная производная сферически усредненной плотности, вычисленная в любом ядре, равна удвоенной плотности в этом ядре, умноженной на отрицательное значение атомный номер ().
Асимптотическое поведение
Условие ядерного возврата обеспечивает околоядерную (малую ) поведение плотности как
Дальний (большой ) также известно поведение плотности, имеющее вид[5]
где я энергия ионизации системы.
Плотность отклика
Другое более общее определение плотности - это «плотность линейного отклика».[6][7] Это плотность, которая при сжатии с любым одноэлектронным свободным от спина оператором дает соответствующее свойство, определяемое как производная энергии. Например, дипольный момент является производной энергии по внешнему магнитному полю, а не математическое ожидание оператора над волновой функцией. Для некоторых теорий они одинаковы, когда волновая функция сходится. Числа заполнения не ограничиваются диапазоном от нуля до двух, и поэтому иногда даже плотность отклика может быть отрицательной в определенных областях пространства.[8]
Обзор
В молекулы, области с большой электронной концентрацией обычно находятся вокруг атом, и его облигации. В де-локализованном или сопряженные системы, Такие как фенол, бензол и такие соединения, как гемоглобин и хлорофиллэлектронная плотность значительна во всей области, т.е. в бензоле они находятся выше и ниже плоского кольца. Иногда это изображают схематически как серию чередующихся одинарных и двойных связей. В случае фенола и бензола кружок внутри шестиугольник показывает делокализованную природу соединения. Это показано ниже:
В соединениях с множественными кольцевыми системами, которые связаны между собой, это уже неточно, поэтому используются чередующиеся одинарные и двойные связи. В таких соединениях, как хлорофилл и фенол, на некоторых диаграммах показана пунктирная или пунктирная линия, обозначающая делокализацию областей, где электронная плотность выше рядом с одинарными связями.[9] Сопряженные системы иногда могут представлять регионы, где электромагнитное излучение поглощается на разных длинах волн, что приводит к окрашиванию соединений. В полимеры, эти области известны как хромофоры.
В квантово-химические расчеты, электронная плотность ρ (р), является функцией координат р, определенную так ρ (р) dр - количество электронов в малом объеме dр. За закрытая оболочка молекулы можно записать в виде суммы произведений базисных функций φ:
где P - матрица плотности. Плотность электронов часто выражается в терминах изоповерхности (поверхности изоплотности) с размером и формой поверхности, определяемыми значением выбранной плотности или в терминах процента от общего количества заключенных электронов.
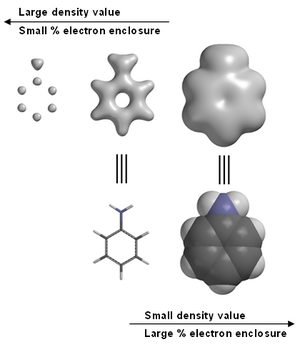
Программное обеспечение для молекулярного моделирования часто предоставляет графические изображения электронной плотности. Например, в анилин (см. изображение справа). Графические модели, в том числе электронная плотность, широко используются в химическом образовании.[10] Обратите внимание, что на крайнем левом изображении анилина высокие концентрации электронов связаны с угли и азот, но водород с одним протоном в ядрах не видны. Это причина того, что дифракция рентгеновских лучей испытывает трудности с поиском позиций водорода.
Большинство пакетов программного обеспечения для молекулярного моделирования позволяют пользователю выбирать значение электронной плотности, часто называемое изозначением. Некоторое программное обеспечение[11] также позволяет указать электронную плотность в процентах от общего количества заключенных электронов. В зависимости от значения (типичные единицы - электроны на куб. Бор), или процент от общего количества заключенных электронов, поверхность электронной плотности может быть использована для определения местоположения атомов, подчеркивая электронную плотность, связанную с химические связи или для обозначения общего размера и формы молекулы.[12]
Графически поверхность электронной плотности также служит холстом, на котором могут отображаться другие электронные свойства. Карта электростатического потенциала (свойство электростатический потенциал отображается на электронной плотности) является индикатором распределения заряда в молекуле. Карта локального ионизационного потенциала (свойство потенциал локальной ионизации нанесенная на карту по электронной плотности) обеспечивает индикатор электрофильности. И карта LUMO (самая низкая незанятая молекулярная орбиталь нанесенная на карту электронной плотности) может указывать на нуклеофильность.[13]
Эксперименты
Многие экспериментальные методы позволяют измерять электронную плотность. Например, квантовая кристаллография через дифракция рентгеновских лучей сканирование, при котором рентгеновские лучи подходящей длины волны направляются на образец, а измерения производятся с течением времени, дает вероятностное представление о местонахождении электронов. С этих позиций часто можно определить молекулярные структуры, а также точное распределение плотности заряда кристаллизованных систем. Квантовая электродинамика и некоторые отрасли квантовая теория также изучать и анализировать электрон суперпозиция и другие связанные явления, такие как Индекс NCI что позволяет изучать нековалентные взаимодействия с использованием электронной плотности. Анализ населения Малликена основан на плотности электронов в молекулах и представляет собой способ деления плотности между атомами, чтобы дать оценку атомных зарядов.
В просвечивающая электронная микроскопия (ТЕА) и глубоконеупругое рассеяние, а также другие частица высокой энергии В экспериментах электроны высоких энергий взаимодействуют с электронным облаком, чтобы дать прямое представление о плотности электронов. ТЕМ, сканирующая туннельная микроскопия (СТМ) и атомно-силовая микроскопия (AFM) можно использовать для исследования электронной плотности отдельных атомов.[нужна цитата]
Плотность отжима
Плотность отжима электронная плотность, приложенная к свободные радикалы. Он определяется как полная электронная плотность электронов одного спина за вычетом общей электронной плотности электронов другого спина. Один из способов экспериментального измерения - электронный спиновой резонанс,[14] Дифракция нейтронов позволяет напрямую отображать спиновую плотность в 3D-пространстве.
Смотрите также
- Карта разницы плотности
- Электронное облако
- Электронная конфигурация
- Разрешение (электронная плотность)
- Плотность заряда
- Функциональная теория плотности
- Вероятность тока
Рекомендации
- ^ Парр, Роберт Дж .; Ян, Вэйтао (1989). Плотностно-функциональная теория атомов и молекул. Нью-Йорк: Издательство Оксфордского университета. ISBN 978-0-19-509276-9.
- ^ Либ, Эллиотт Х. (1983). «Функционалы плотности для кулоновских систем». Международный журнал квантовой химии. 24 (3): 243–277. Дои:10.1002 / qua.560240302.
- ^ Эйерс, Пол У .; Парр, Роберт Г. (2003). «Достаточное условие монотонного спада электронной плотности в многоэлектронных системах». Международный журнал квантовой химии. 95 (6): 877–881. Дои:10.1002 / qua.10622.
- ^ Като, Тосио (1957). «О собственных функциях систем многих частиц в квантовой механике». Сообщения по чистой и прикладной математике. 10 (2): 151–177. Дои:10.1002 / cpa.3160100201.
- ^ Моррелл, Мэрилин М .; Парр, Роберт. ГРАММ.; Леви, Мел (1975). «Расчет потенциалов ионизации по матрицам плотности и естественным функциям, а также дальнодействию естественных орбиталей и электронной плотности». Журнал химической физики. 62 (2): 549–554. Bibcode:1975ЖЧФ..62..549М. Дои:10.1063/1.430509.
- ^ Хэнди, Николас С .; Шефер, Генри Ф. (1984). «Об оценке аналитических производных энергии для коррелированных волновых функций». Журнал химической физики. 81 (11): 5031–5033. Bibcode:1984ЖЧФ..81.5031Н. Дои:10.1063/1.447489.
- ^ Wiberg, Kenneth B .; Хадад, Кристофер М .; Лепаж, Тереза Дж .; Бренеман, Курт М .; Фриш, Майкл Дж. (1992). «Анализ влияния электронной корреляции на распределение плотности заряда». Журнал физической химии. 96 (2): 671–679. Дои:10.1021 / j100181a030.
- ^ Гордон, Марк С .; Шмидт, Майкл В .; Чабан, Галина М .; Glaesemann, Kurt R .; Стивенс, Уолтер Дж .; Гонсалес, Карлос (1999). «Естественная орбитальная диагностика многоконфигурации в коррелированных волновых функциях». J. Chem. Phys. 110 (9): 4199–4207. Bibcode:1999ЖЧФ.110.4199Г. Дои:10.1063/1.478301.
- ^ например, белая линия на диаграмме на Хлорофиллы и каротиноиды В архиве 2017-08-09 в Wayback Machine
- ^ Алан Дж. Шустерман и Гвендолин П. Шустерман (1997). «Преподавание химии с использованием моделей электронной плотности». Журнал химического образования. 74 (7): 771–775. Bibcode:1997JChEd..74..771S. Дои:10.1021 / ed074p771.CS1 maint: использует параметр авторов (связь)
- ^ или, например, программа Spartan от Wavefunction, Inc.
- ^ Уоррен Дж. Хере, Алан Дж. Шустерман, Джанет Э. Нельсон (1998). Рабочая тетрадь молекулярного моделирования для органической химии. Ирвин, Калифорния: Wavefunction, Inc., стр. 61–86. ISBN 978-1-890661-18-2.CS1 maint: использует параметр авторов (связь)
- ^ Хере, Уоррен Дж. (2003). Руководство по молекулярной механике и квантово-химическим расчетам. Ирвин, Калифорния: Wavefunction, Inc., стр. 85–100. ISBN 978-1-890661-06-9.
- ^ ИЮПАК, Сборник химической терминологии, 2-е изд. («Золотая книга») (1997). Исправленная онлайн-версия: (2006–) "плотность вращения". Дои:10.1351 / goldbook.S05864