WikiDer > F-число
Эта статья ведущий раздел не адекватно подвести итог ключевые моменты его содержания. Пожалуйста, подумайте о расширении интереса до предоставить доступный обзор обо всех важных аспектах статьи. (Декабрь 2018 г.) |
В оптика, то f-число оптической системы, такой как объектив это соотношение системы фокусное расстояние к диаметру вступительный ученик ("Чисто отверстие").[1][2][3] Он также известен как фокусное отношение, f-соотношение, или f-stop, и это очень важно в фотография.[4] Это безразмерное число это количественная мера светосила; увеличение числа f называется остановка. Число f обычно указывается в нижнем регистре. на крючке f с форматом ж/N, где N это f-число.
Число f - это взаимный из относительная апертура (диаметр апертуры, деленный на фокусное расстояние).[5]
Обозначение
Число f N дан кем-то:
где это фокусное расстояние, и диаметр входного зрачка (эффективная апертура). Принято писать f-числа перед ж/, который формирует математическое выражение диаметра входного зрачка через ж и N.[1] Например, если линза ' фокусное расстояние - 10 мм, диаметр входного зрачка - 5 мм, f-число - 2. Это будет выражаться как "ж/ 2 "в системе линз. Диаметр апертуры будет равен .
Большинство линз имеют регулируемый диафрагма, который изменяет размер диафрагма и, следовательно, размер входного зрачка. Это позволяет практикующему изменять число f в соответствии с потребностями. Следует понимать, что диаметр входного зрачка не обязательно равен диаметру диафрагмы из-за увеличивающего эффекта линзовых элементов перед апертурой.
Игнорируя различия в эффективности светопропускания, объектив с большим числом f проецирует более темные изображения. Яркость проецируемого изображения (освещенность) относительно яркости сцены в поле зрения объектива (яркость) убывает пропорционально квадрату f-числа. Фокусное расстояние 100 мм ж/ 4 имеет диаметр входного зрачка 25 мм. Фокусное расстояние 100 мм ж/ 2 имеет диаметр входного зрачка 50 мм. Поскольку площадь изменяется пропорционально квадрату диаметра зрачка,[6] количество света, допускаемого ж/ 2 в четыре раза больше, чем у ж/ 4 линзы. Чтобы получить такой же фотографическая экспозиция, время экспозиции должно быть уменьшено в четыре раза.
Фокусное расстояние 200 мм ж/ 4 имеет диаметр входного зрачка 50 мм. Входной зрачок объектива 200 мм в четыре раза больше, чем 100 мм. ж/ 4 входного зрачка объектива и, таким образом, собирает в четыре раза больше света от каждого объекта в поле зрения объектива. Но по сравнению со 100-миллиметровым объективом, 200-миллиметровый объектив проецирует изображение каждого объекта в два раза выше и в два раза шире, покрывая в четыре раза большую площадь, и поэтому обе линзы производят одинаковую освещенность в фокальной плоскости при отображении сцены заданная яркость.
А Т-стоп - f-число, скорректированное с учетом эффективности пропускания света.
Остановки, условные значения диафрагмы и выдержка
Слово Стоп иногда сбивает с толку из-за множества значений. Остановка может быть физическим объектом: непрозрачной частью оптической системы, которая блокирует определенные лучи. В диафрагма это настройка диафрагмы, которая ограничивает яркость изображения, ограничивая размер входного зрачка, в то время как полевая остановка это ограничитель, предназначенный для отключения света, который находится за пределами желаемого поля зрения и может вызвать блики или другие проблемы, если его не остановить.
В фотографии остановки также единица измерения используется для количественной оценки соотношений света или экспозиции, при этом каждая добавленная ступень означает коэффициент два, а каждая вычтенная ступень означает коэффициент 1/2. Универсальное устройство также известно как EV (значение экспозиции) единица измерения. На фотоаппарате установка диафрагмы традиционно регулируется дискретными шагами, известными как f-стопы. Каждый "Стоп"отмечен соответствующим числом f и представляет собой уменьшение наполовину интенсивности света по сравнению с предыдущей остановкой. Это соответствует уменьшению диаметра зрачка и диафрагмы в раз или около 0,7071, и, следовательно, уменьшение площади зрачка вдвое.
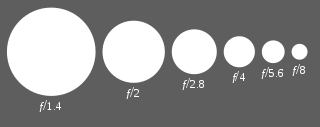
В большинстве современных объективов используется стандартная шкала диафрагмы, которая составляет примерно геометрическая последовательность чисел, что соответствует последовательности полномочия из квадратный корень из 2: ж/1, ж/1.4, ж/2, ж/2.8, ж/4, ж/5.6, ж/8, ж/11, ж/16, ж/22, ж/32, ж/45, ж/64, ж/90, ж/ 128 и т. Д. Каждый элемент в последовательности на одну ступень ниже, чем элемент слева от него, и на одну ступень выше, чем элемент справа. Значения соотношений округлены до этих конкретных условных чисел, чтобы их было легче запомнить и записать. Последовательность, указанная выше, получается путем аппроксимации следующей точной геометрической последовательности:
Точно так же, как одна диафрагма соответствует двукратному значению силы света, выдержка расположены так, что каждая настройка отличается по продолжительности примерно в два раза от своей соседней. Открытие линзы на одну ступень позволяет вдвое больше света попадать на пленку за определенный период времени. Следовательно, чтобы получить такую же экспозицию на этой большей диафрагме, что и на предыдущей диафрагме, затвор будет открыт на половину меньшего времени (т. Е. С удвоенной скоростью). Пленка будет одинаково реагировать на это равное количество света, поскольку она обладает свойством взаимность. Это менее верно для очень длинных или коротких выдержек, когда у нас нарушение взаимности. Диафрагма, выдержка и чувствительность пленки связаны: для постоянной яркости сцены удвоение области диафрагмы (одна ступень), уменьшение вдвое скорости затвора (удвоение времени открытия) или использование пленки в два раза более чувствительной, оказывает такое же влияние на экспонированное изображение. Для всех практических целей особая точность не требуется (механические выдержки были заведомо неточными, поскольку износ и смазка менялись, не влияя на экспозицию). Неважно, что площади диафрагмы и выдержка не различаются ровно в два раза.
Фотографы иногда высказывают другое воздействие отношения в терминах «стопов». Игнорируя маркировку числа f, диафрагма делает логарифмическая шкала интенсивности воздействия. Учитывая эту интерпретацию, можно подумать о том, чтобы сделать полшага по этой шкале, чтобы сделать разницу в экспозиции «полустопа».
Дробные остановки
Большинство фотоаппаратов двадцатого века имели непрерывно изменяемую диафрагму, используя ирисовая диафрагма, с каждой отмеченной точкой. Апертура с остановкой щелчка стала широко использоваться в 1960-х годах; шкала диафрагмы обычно имела щелчок через каждые полторы ступени.
В современных камерах, особенно когда диафрагма установлена на корпусе камеры, f-число часто делится более точно, чем шаги в одну ступень. Шаги 1/3 остановки (1⁄3 EV) являются наиболее распространенными, так как это соответствует системе ISO скорость пленки. На некоторых камерах используются ступени с полустопом. Обычно отмечаются точки и щелкаются промежуточные позиции. Например, апертура на треть меньше, чем ж/2,8 равно ж/3.2, на две трети меньше ж/3.5, а на целую ступень меньше ж/ 4. Следующие несколько диафрагм в этой последовательности:
- ж/4.5, ж/5, ж/5.6, ж/6.3, ж/7.1, ж/ 8 и др.
Для расчета шагов с полной остановкой (1 EV) можно использовать
- 20×0.5, 21×0.5, 22×0.5, 23×0.5, 24×0.5 и т.п.
Шаги в полустоп (1⁄2 EV) будет
- 20/2×0.5, 21/2×0.5, 22/2×0.5, 23/2×0.5, 24/2×0.5 и т.п.
Шаги на третьей остановке (1⁄3 EV) будет
- 20/3×0.5, 21/3×0.5, 22/3×0.5, 23/3×0.5, 24/3×0.5 и т.п.
Как и в более ранних стандартах светочувствительности пленки DIN и ASA, чувствительность ISO определяется только с шагом в одну треть ступени, а выдержки цифровых камер обычно находятся в одном масштабе в обратных секундах. Часть диапазона ISO - это последовательность
- ... 16/13°, 20/14°, 25/15°, 32/16°, 40/17°, 50/18°, 64/19°, 80/20°, 100/21°, 125/22°...
в то время как выдержки в обратных секундах имеют несколько условных различий в своих числах (1⁄15, 1⁄30, и1⁄60 второй вместо1⁄16, 1⁄32, и1⁄64).
На практике максимальная диафрагма объектива часто не соответствует действительности. интеграл сила √2 (т.е. √2 в степени целого числа), и в этом случае это обычно половина или треть ступени выше или ниже целой степени √2.
Современные сменные объективы с электронным управлением, такие как те, что используются для зеркальных фотоаппаратов, имеют внутреннее значение диафрагмы1⁄8-остановить приращения, поэтому камеры1⁄3-установки остановок приблизительны1⁄8-остановка установки в объектив.
Стандартная шкала f-числа с полной остановкой
В том числе значение диафрагмы СРЕДНИЙ:
Обычные и рассчитанные f-числа, точные серии:
| средний | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 0.5 | 0.7 | 1.0 | 1.4 | 2 | 2.8 | 4 | 5.6 | 8 | 11 | 16 | 22 | 32 | 45 | 64 | 90 | 128 | 180 | 256 |
| рассчитанный | 0.5 | 0.707... | 1.0 | 1.414... | 2.0 | 2.828... | 4.0 | 5.657... | 8.0 | 11.31... | 16.0 | 22.62... | 32.0 | 45.25... | 64.0 | 90.51... | 128.0 | 181.02... | 256.0 |
Типичная шкала f-числа с половиной ступени
| средний | −1 | −0.5 | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | 9 | 9.5 | 10 | 10.5 | 11 | 11.5 | 12 | 12.5 | 13 | 13.5 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 0.7 | 0.8 | 1.0 | 1.2 | 1.4 | 1.7 | 2 | 2.4 | 2.8 | 3.3 | 4 | 4.8 | 5.6 | 6.7 | 8 | 9.5 | 11 | 13 | 16 | 19 | 22 | 27 | 32 | 38 | 45 | 54 | 64 | 76 | 90 | 107 | 128 |
Типичная шкала f-числа с точностью до одной трети ступени
| средний | −1 | −0.7 | −0.3 | 0 | 0.3 | 0.7 | 1 | 1.3 | 1.7 | 2 | 2.3 | 2.7 | 3 | 3.3 | 3.7 | 4 | 4.3 | 4.7 | 5 | 5.3 | 5.7 | 6 | 6.3 | 6.7 | 7 | 7.3 | 7.7 | 8 | 8.3 | 8.7 | 9 | 9.3 | 9.7 | 10 | 10.3 | 10.7 | 11 | 11.3 | 11.7 | 12 | 12.3 | 12.7 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 0.7 | 0.8 | 0.9 | 1.0 | 1.1 | 1.2 | 1.4 | 1.6 | 1.8 | 2 | 2.2 | 2.5 | 2.8 | 3.2 | 3.5 | 4 | 4.5 | 5.0 | 5.6 | 6.3 | 7.1 | 8 | 9 | 10 | 11 | 13 | 14 | 16 | 18 | 20 | 22 | 25 | 29 | 32 | 36 | 40 | 45 | 51 | 57 | 64 | 72 | 80 | 90 |
Иногда одно и то же число входит в несколько шкал; например, апертура ж/1.2 может использоваться как в полустопе[7]или система 1/3 ступени;[8]иногда ж/1.3 и ж/3.2 и другие различия используются для шкалы в одну треть ступени.[9]
Типичная шкала f-числа с шагом 1/4 ступени
| средний | 0 | 0.25 | 0.5 | 0.75 | 1 | 1.25 | 1.5 | 1.75 | 2 | 2.25 | 2.5 | 2.75 | 3 | 3.25 | 3.5 | 3.75 | 4 | 4.25 | 4.5 | 4.75 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.7 | 1.8 | 2 | 2.2 | 2.4 | 2.6 | 2.8 | 3.1 | 3.3 | 3.7 | 4 | 4.4 | 4.8 | 5.2 | 5.6 |
| Минолта | 1.00 | 1.01 | 1.02 | 1.03 | 1.40 | 1.41 | 1.42 | 1.43 | 2.00 | 2.01 | 2.02 | 2.03 | 2.80 | 2.81 | 2.82 | 2.83 | 4.00 | 4.01 | 4.02 | 4.03 | 5.60 |
| средний | 5 | 5.25 | 5.5 | 5.75 | 6 | 6.25 | 6.5 | 6.75 | 7 | 7.25 | 7.5 | 7.75 | 8 | 8.25 | 8.5 | 8.75 | 9 | 9.25 | 9.5 | 9.75 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 5.6 | 6.2 | 6.7 | 7.3 | 8 | 8.7 | 9.5 | 10 | 11 | 12 | 14 | 15 | 16 | 17 | 19 | 21 | 22 | 25 | 27 | 29 | 32 |
| Минолта | 5.60 | 5.61 | 5.62 | 5.63 | 8.00 | 8.01 | 8.02 | 8.03 | 110 | 111 | 112 | 113 | 160 | 161 | 162 | 163 | 220 | 221 | 222 | 223 | 320 |
H-стоп
An H-стоп (для отверстия, по соглашению пишется с заглавной буквы H) - это эквивалент числа f для эффективной экспозиции, основанный на площади, покрытой отверстиями в диффузионные диски или отверстие сита нашел в Rodenstock Imagon линзы.
Т-стоп
А Т-стоп (для остановок передачи, по соглашению пишется с заглавной буквы T) - это f-число, скорректированное с учетом эффективности передачи света (коэффициент пропускания). Объектив с Т-стопом N проецирует изображение такой же яркости, как у идеального объектива, с коэффициентом пропускания 100% и f-числом N. Конкретный объектив T-stop, Т, получается делением числа f на квадратный корень из коэффициента пропускания этой линзы:
Например, жОбъектив /2.0 с коэффициентом пропускания 75% имеет Т-стоп 2.3:
Поскольку реальные линзы имеют коэффициент пропускания менее 100%, число Т-стопа всегда больше, чем его число f.[10]
С потерей 8% на поверхность воздушного стекла на линзах без покрытия, многослойное покрытие линз является ключевым моментом в конструкции линз для уменьшения потерь линз на пропускание. В некоторых обзорах объективов измеряется t-стоп или скорость передачи в своих тестах.[11][12]Т-стопы иногда используются вместо f-чисел для более точного определения экспозиции, особенно при использовании внешних световые метры.[13] Типичный коэффициент пропускания линз составляет 60–95%.[14] Т-стопы часто используются в кинематографии, где многие изображения просматриваются в быстрой последовательности и даже небольшие изменения в экспозиции будут заметны. Объективы кинокамер обычно калибруются по Т-ступеням, а не по диафрагмам.[13] В фотосъемке, без необходимости строгого согласования всех используемых объективов и камер, небольшие различия в экспозиции менее важны; однако Т-стопы все еще используются в некоторых типах объективов специального назначения, таких как Плавный трансфокус линзы от Минолта и Sony.
Солнечное 16 правило
Примером использования f-чисел в фотографии является солнечное правило 16: примерно правильная экспозиция будет получена в солнечный день при использовании диафрагмы ж/ 16 и выдержка, ближайшая к чувствительности ISO пленки; например, при использовании пленки ISO 200 диафрагма ж/ 16 и выдержка1⁄200 второй. Затем число f можно отрегулировать вниз для ситуаций с недостаточным освещением. Выбор меньшего числа f означает «раскрытие» объектива. Выбор большего числа f означает «закрытие» или «остановку» объектива.
Влияние на резкость изображения
Глубина резкости увеличивается с увеличением числа f, как показано на изображении здесь. Это означает, что фотографии, сделанные с малым числом f (большой диафрагмой), будут иметь тенденцию иметь объекты на одном расстоянии в фокусе, а остальная часть изображения (более близкие и дальние элементы) не в фокусе. Это часто используется для фотография природы и портретная живопись потому что размытие фона (эстетическое качество, известное как 'боке') может быть эстетически приятным и фокусирует внимание зрителя на главном объекте на переднем плане. В глубина резкости изображения, созданного с заданным f-числом, также зависит от других параметров, включая фокусное расстояние, расстояние до объекта и формат пленки или датчика, использованного для захвата изображения. Глубину резкости можно описать как зависящую только от угла зрения, расстояния до объекта и вступительный ученик диаметр (как в метод фон Рора). В результате меньшие форматы будут иметь более глубокое поле, чем большие форматы при том же диафрагменном числе, на том же расстоянии фокусировки и одинаковом расстоянии. угол обзора поскольку для меньшего формата требуется более короткое фокусное расстояние (более широкоугольный объектив) для получения того же угла обзора, а глубина резкости увеличивается с более короткими фокусными расстояниями. Следовательно, эффекты уменьшенной глубины резкости потребуют меньших значений диафрагмы (и, следовательно, потенциально более сложной или сложной оптики) при использовании камер малого формата, чем при использовании камер большего формата.
Резкость изображения связана с диафрагменным числом через два различных оптических эффекта: аберрация, из-за несовершенной конструкции линз, и дифракция что связано с волновой природой света.[15] Оптимальное значение диафрагмы для размытия зависит от конструкции объектива. Для современных стандартных объективов с 6 или 7 элементами самый острый изображение часто получается вокруг ж/5.6–ж/ 8, в то время как для старых стандартных объективов, имеющих только 4 элемента (Формула Тессара) останавливаясь ж/ 11 даст самое резкое изображение[нужна цитата]. Большее количество элементов в современных объективах позволяет дизайнеру компенсировать аберрации, позволяя объективу давать более качественные изображения при меньших числах f. Даже если аберрации сведены к минимуму с помощью лучших линз, дифракция создает некоторое распространение лучей, вызывая расфокусировку. Чтобы компенсировать это, используйте максимально возможный диаметр отверстия объектива (а не само диафрагменное число).
Ослабление света также чувствительно к диафрагме. Многие широкоугольные объективы демонстрируют значительное ослабление света (виньетирование) по краям для больших отверстий.
Фотожурналисты есть поговорка "ж/ 8 и будь там", что означает, что быть на месте происшествия важнее, чем беспокоиться о технических деталях. На практике ж/ 8 обеспечивает адекватную глубину резкости и достаточную светосилу для хорошей базовой экспозиции в большинстве дневных ситуаций.[16]
Человеческий глаз
Вычисление f-числа человеческий глаз включает в себя вычисление физической апертуры и фокусного расстояния глаза. Зрачок может достигать 6–7 мм в ширину, что соответствует максимальной физической апертуре.
F-число человеческого глаза варьируется от примерно ж/ 8,3 в очень ярко освещенном месте примерно до ж/2.1 в темноте.[17] Для вычисления фокусного расстояния необходимо учитывать светоотражающие свойства жидкости в глазу. Если рассматривать глаз как обычную камеру и объектив, заполненные воздухом, получается другое фокусное расстояние, что приводит к неправильному числу f.
Токсичные вещества и яды (подобно атропин) позволяет значительно сократить диапазон диафрагмы. Фармацевтические препараты, такие как глазные капли, также могут вызывать аналогичные побочные эффекты. Тропикамид и фенилэфрин используются в медицине как мидриатики для расширения зрачков при обследовании сетчатки и хрусталика. Эти лекарства начинают действовать примерно через 30–45 минут после закапывания и действуют примерно 8 часов. Атропин также используется таким образом, но его действие может длиться до 2 недель, наряду с мидриатическим эффектом; он производит циклоплегия (состояние, при котором хрусталик глаза не может фокусироваться на близких объектах). Этот эффект проходит через 8 часов. Другие лекарства дают обратный эффект. Пилокарпин - миотик (вызывает миоз); в зависимости от человека и его глазных характеристик зрачок может уменьшиться до 1 мм в диаметре. Такие капли используются в некоторых глаукома пациентам для предотвращения приступов острой глаукомы.
Фокусное отношение в телескопах

В астрономии число f обычно называют числом фокусное отношение (или f-соотношение) обозначенный как . Он по-прежнему определяется как фокусное расстояние из задача деленный на его диаметр или диаметром отверстие остановка в системе:
Несмотря на то, что принципы фокусного соотношения всегда одни и те же, применение этого принципа может отличаться. В фотография фокусное отношение изменяет освещенность в фокальной плоскости (или оптическую силу на единицу площади изображения) и используется для управления такими переменными, как глубина резкости. При использовании оптический телескоп В астрономии нет проблемы глубины резкости, а яркость точечных звездных источников в терминах полной оптической мощности (не деленной на площадь) является функцией только абсолютной площади апертуры, независимо от фокусного расстояния. Фокусное расстояние определяет поле зрения инструмента и масштаб изображения, которое отображается в фокальной плоскости до окуляр, пленочная пластина или CCD.
Например, SOAR 4-метровый телескоп имеет небольшое поле зрения (~ж/ 16), что полезно для изучения звезд. В LSST Телескоп длиной 8,4 м, который будет покрывать все небо каждые три дня, имеет очень большое поле зрения. Его короткое фокусное расстояние 10,3 м (ж/1.2) стало возможным благодаря системе коррекции ошибок, которая включает вторичные и третичные зеркала, трехэлементную рефракционную систему, активную опору и оптику.[18]
Уравнение камеры (G #)
Уравнение камеры или G # - это соотношение сияние достигнув датчика камеры к сияние в фокальной плоскости объектив.[19]
τ - коэффициент пропускания линзы, единицы - sr−1.
Рабочее число f
Число f точно описывает способность линзы собирать свет только для объектов, находящихся на бесконечном расстоянии.[20] Это ограничение обычно игнорируется в фотографии, где f-число часто используется независимо от расстояния до объекта. В оптический дизайн, альтернатива часто требуется для систем, в которых объект находится недалеко от объектива. В этих случаях рабочее f-число используется. Рабочее число f Nш дан кем-то:[20]
- ,
где N - нескорректированное f-число, NAя это изображение-пространство числовая апертура линзы, это абсолютная величина объектива увеличение для объекта на определенном расстоянии, и п это увеличение зрачка. Поскольку увеличение зрачка редко известно, его часто принимают равным 1, что является правильным значением для всех симметричных линз.
В фотографии это означает, что по мере приближения фокусировки эффективная диафрагма объектива становится меньше, что делает экспозицию темнее. Рабочее число f часто описывается в фотографии как число f, скорректированное с учетом удлинения объектива коэффициент сильфона. Это особенно важно в макросъемка.
История
Система f-чисел для указания относительной апертуры появилась в конце девятнадцатого века, конкурируя с несколькими другими системами обозначения апертуры.
Происхождение относительной апертуры
В 1867 году Саттон и Доусон определили «апертальное отношение» как величину, обратную современному f-числу. В следующей цитате "апертальное соотношение"1⁄24"рассчитывается как отношение 6 дюймов (150 мм) к 1⁄4 дюйма (6,4 мм), что соответствует ж/ 24 диафрагма:
В каждой линзе есть, соответствующая заданному апертальному отношению (то есть отношению диаметра диафрагмы к фокусному расстоянию), определенное расстояние от ближнего объекта от него, между которым и бесконечностью все объекты находятся в одинаковом хорошем состоянии. фокус. Например, в однообъективном объективе с фокусом 6 дюймов, с1⁄4 дюйм. стопа (апертальное отношение одна-двадцать четвертая), все объекты, расположенные на расстоянии между 20 футами от линзы и на бесконечном расстоянии от нее (например, неподвижная звезда), одинаково хорошо сфокусированы. Поэтому двадцать футов называются «фокусным диапазоном» объектива, когда используется этот стоп. Следовательно, диапазон фокусировки - это расстояние до ближайшего объекта, который будет хорошо сфокусирован, если матовое стекло настроено на очень удаленный объект. В одном и том же объективе диапазон фокусировки будет зависеть от размера используемой диафрагмы, в то время как в разных объективах с одинаковым апертальным отношением диапазоны фокусных расстояний будут больше при увеличении фокусного расстояния объектива. Термины «апертальное отношение» и «фокусное расстояние» не вошли в общий обиход, но очень желательно, чтобы они вошли в употребление, чтобы предотвратить двусмысленность и неопределенность при рассмотрении свойств фотографических линз.[21]
В 1874 г. Джон Генри Даллмейер называется отношением «коэффициент яркости» линзы:
В быстрота линзы зависит от отношения или отношения апертуры к эквивалентному фокусу. Чтобы убедиться в этом, разделите эквивалентный фокус по диаметру фактического рабочая апертура рассматриваемого объектива; и запишите частное как знаменатель с 1 или единицей для числителя. Таким образом, чтобы найти соотношение линзы диаметром 2 дюйма и фокусировки 6 дюймов, разделите фокус на диафрагму, или 6, разделенное на 2, равно 3; т.е.1⁄3 - соотношение интенсивностей.[22]
Хотя у него еще не было доступа к Эрнст Аббетеория остановок и учеников,[23] который был широко доступен Зигфрид Чапски в 1893 г.,[24] Даллмейер знал, что его рабочая апертура был не таким, как физический диаметр диафрагмы:
Однако следует отметить, что для нахождения настоящего соотношение интенсивностинеобходимо определить диаметр фактического рабочего отверстия. Это легко сделать в случае использования одинарных линз или двойных комбинированных линз, используемых с полным открытием, для этого просто требуется применение пары циркуля или линейки; но когда используются двойные или тройные комбинированные линзы со вставленными упорами между комбинации, это несколько хлопотнее; поскольку очевидно, что в этом случае диаметр используемого ограничителя не является мерой действительного пучка света, пропускаемого передней комбинацией. Чтобы в этом убедиться, сфокусируйтесь на удаленном объекте, снимите фокусирующий экран и замените его коллодиевым слайдом, предварительно вставив кусок картона вместо подготовленной пластины. Сделайте маленькое круглое отверстие в центре картона с помощью пирсера, а теперь переместите в затемненную комнату; поставьте свечу близко к отверстию и посмотрите на подсвеченный участок, видимый на передней комбинации; тщательно измеренный диаметр этого круга и есть фактическая рабочая апертура рассматриваемой линзы для конкретного используемого упора.[22]
Этот момент был дополнительно подчеркнут Чапским в 1893 году.[24] Согласно английскому обзору его книги в 1894 году, «настоятельно настаивает на необходимости четко различать эффективную апертуру и диаметр физического упора».[25]
Сын Дж. Х. Даллмейера, Томас Рудольфус Даллмейер, изобретатель телеобъектива, вслед за соотношение интенсивности терминологии в 1899 г.[26]
Системы нумерации апертур
В то же время был разработан ряд систем нумерации диафрагмы с целью заставить время экспозиции изменяться прямо или обратно пропорционально диафрагме, а не квадрату числа f или обратному квадрату апертального отношения или интенсивности. соотношение. Но все эти системы включают некоторую произвольную константу, в отличие от простого соотношения фокусного расстояния и диаметра.
Например, Единая система (США) апертур был принят в качестве стандарта Фотографическое общество Великобритании в 1880-х гг. Ботамли в 1891 году сказал, что «остановки всех лучших производителей теперь расположены по этой системе».[27] У US 16 такая же апертура, как у ж/ 16, но отверстия, которые больше или меньше на точку, используют удвоение или уменьшение вдвое номера США, например ж/ 11 - это США 8 и ж/ 8 - это США 4. Требуемое время экспонирования прямо пропорционально числу в США. Eastman Kodak использовали американские остановки на многих своих камерах, по крайней мере, в 1920-х годах.
К 1895 году Ходжес противоречит Ботамли, говоря, что система f-чисел взяла верх: «Это называется ж/Икс системы, и так отмечены диафрагмы всех современных объективов хорошей конструкции ».[28]
Вот ситуация, увиденная в 1899 году:
Пайпер в 1901 году[29] обсуждает пять различных систем маркировки диафрагмы: старая и новая Zeiss системы, основанные на фактической интенсивности (пропорциональной обратному квадрату f-числа); и системы США, C.I. и Даллмейера, основанные на экспозиции (пропорциональной квадрату числа f). Он называет f-число "числом", "числом светосилы" и "числом апертуры". Он называет такие выражения, как ж/ 8 «дробный диаметр» апертуры, хотя он буквально равен «абсолютному диаметру», который он выделяет как другой термин. Он также иногда использует такие выражения, как «апертура f 8» без деления, обозначенного косой чертой.
Бек и Эндрюс в 1902 году говорят о стандарте Королевского фотографического общества. ж/4, ж/5.6, ж/8, ж/11.3 и др.[30] R.P.S. сменили название и покинули американскую систему где-то между 1895 и 1902 годами.
Типографская стандартизация

К 1920 г. срок f-число появился в книгах как Номер F и f / число. В современных публикациях формы f-число и число f более распространены, хотя более ранние формы, а также F-число все еще встречаются в нескольких книгах; нередко начальные строчные буквы ж в f-число или f / число набирается курсивом с крючками: ж, или ж.[31]
Обозначения для f-чисел также были весьма разнообразными в начале двадцатого века. Иногда их писали с большой буквы,[32] иногда с точкой (точкой) вместо косой черты,[33] и иногда устанавливается как вертикальная дробь.[34]
1961 год КАК стандарт PH2.12-1961 Фотографические экспонометры общего назначения американского стандарта (фотоэлектрические) указывает, что «Обозначение относительных отверстий должно быть f / или ж : затем следует эффективный ж-число ". Они показывают курсивом с крючками. ж не только в символе, но и в термине f-число, который сегодня чаще выделяется обычным шрифтом без курсива.
Смотрите также
- Круг замешательства
- Группа f / 64
- Фотографический дизайн объектива
- Камеры-обскуры
- Предпочтительный номер
использованная литература
- ^ а б Смит, Уоррен Современная оптическая инженерия, 4-е изд., 2007 г., McGraw-Hill Professional, стр. 183.
- ^ Хехт, Юджин (1987). Оптика (2-е изд.). Эддисон Уэсли. п. 152. ISBN 0-201-11609-X.
- ^ Грейвенкамп, Джон Э. (2004). Полевое руководство по геометрической оптике. SPIE Field Guides vol. FG01. Беллингхэм, Вашингтон: SPIE. п. 29. ISBN 9780819452948. OCLC 53896720.
- ^ Смит, Уоррен Современный дизайн линз 2005 Макгроу-Хилл.
- ^ ISO, Фотография. Апертуры и связанные свойства, относящиеся к фотообъективам. Обозначения и размеры, ISO 517: 2008.
- ^ Увидеть Площадь круга.
- ^ Гарри С. Бокс (2003). Справочник специалиста по световому оформлению: осветительное оборудование для пленок, практика и распределение электроэнергии (3-е изд.). Focal Press. ISBN 978-0-240-80495-8.
- ^ Пол Кей (2003). Подводная фотография. Гильдия мастеров-мастеров. ISBN 978-1-86108-322-7.
- ^ Дэвид В. Самуэльсон (1998). Пособие для кинематографистов (2-е изд.). Focal Press. ISBN 978-0-240-51480-2.
- ^ Трансмиссия, светопропускание, DxOMark
- ^ Обзор объектива Sigma 85mm F1.4 Art: новый тест, DxOMark
- ^ Цветопередача в биноклях и линзах - Цвета и пропускание, LensTip.com
- ^ а б "Kodak Motion Picture Camera Films". Eastman Kodak. Ноябрь 2000 г. Архивировано с оригинал на 2002-10-02. Получено 2007-09-02.
- ^ Марианна Оелунд, "Линза Т-стопы", dpreview.com, 2009
- ^ Майкл Джон Лэнгфорд (2000). Базовая фотография. Focal Press. ISBN 0-240-51592-7.
- ^ Леви, Майкл (2001). Выбор и использование классических камер: руководство пользователя по оценке функций, состояния и удобства использования классических камер. Amherst Media, Inc. стр. 163. ISBN 978-1-58428-054-5.
- ^ Хехт, Юджин (1987). Оптика (2-е изд.). Эддисон Уэсли. ISBN 0-201-11609-X. Разд. 5.7.1
- ^ Чарльз Ф. Клавер; и другие. (2007-03-19). «Эталонный дизайн LSST» (PDF). LSST Corporation: 45–50. Архивировано из оригинал (PDF) на 2009-03-06. Получено 2011-01-10. Цитировать журнал требует
| журнал =(Помогите) - ^ Дриггеры, Рональд Г. (2003). Энциклопедия оптической инженерии: Pho-Z, страницы 2049-3050. CRC Press. ISBN 978-0-8247-4252-2. Получено 2020-06-18.
- ^ а б Грейвенкамп, Джон Э. (2004). Полевое руководство по геометрической оптике. SPIE Field Guides vol. FG01. ШПИОН. ISBN 0-8194-5294-7. п. 29.
- ^ Томас Саттон и Джордж Доусон, Словарь по фотографии, Лондон: Sampson Low, Son & Marston, 1867, (стр. 122).
- ^ а б Джон Генри Даллмейер, Фотографические линзы: об их выборе и использовании - специальное издание для американских фотографов, памфлет, 1874 г.
- ^ Саутхолл, Джеймс Пауэлл Кок (1910). «Принципы и методы геометрической оптики: особенности в применении к теории оптических инструментов». Макмиллан: 537.
теория остановок.
Цитировать журнал требует| журнал =(Помогите) - ^ а б Зигфрид Чапски, Theorie der optischen Instrumente, nach Abbe, Бреслау: Trewendt, 1893.
- ^ Генри Крю, "Теория оптических инструментов доктора Чапски" в Астрономия и астрофизика XIII с. 241–243, 1894.
- ^ Томас Р. Даллмейер, Telephotography: элементарный трактат о конструкции и применении телеобъективов., Лондон: Heinemann, 1899.
- ^ К. Х. Ботамли, Илфорд Руководство по фотографии, Лондон: Britannia Works Co. Ltd., 1891.
- ^ Джон А. Ходжес, Фотографические линзы: как выбрать и как использовать, Брэдфорд: Перси Лунд и компания, 1895.
- ^ К. Велборн Пайпер, Первая книга линз: элементарный трактат о действии и использовании фотографической линзы, Лондон: Hazell, Watson and Viney, Ltd., 1901.
- ^ Конрад Бек и Герберт Эндрюс, Фотографические линзы: простой трактат, второе издание, Лондон: R. & J. Beck Ltd., c. 1902 г.
- ^ поиск Гугл
- ^ Айвс, Герберт Юджин (1920). Фотография Самолета (Google). Филадельфия: Дж. Б. Липпинкотт. п. 61. ISBN 9780598722225. Получено 2007-03-12.
- ^ Мис, Чарльз Эдвард Кеннет (1920). Основы фотографии. Eastman Kodak. п. 28. Получено 2007-03-12.
- ^ Дерр, Луи (1906). Фотография для студентов-физиков и химиков (Google). Лондон: Макмиллан. п. 83. Получено 2007-03-12.
внешняя ссылка
| Викискладе есть медиафайлы по теме F-число. |